Chapter 1
The Machine Learning Problem
"In science, we must be interested in things, not in persons." — Marie Curie
Chapter 1 of MLVR provides a comprehensive introduction to the machine learning problem, emphasizing how these foundational concepts can be practically implemented using Rust. The chapter begins by defining what machine learning is and the types of problems it solves. It then explores how to formulate a machine learning problem, from defining input features and target outputs to selecting the right model for the task. The chapter also covers the importance of data representation and feature engineering, key considerations for model selection and evaluation, and the optimization techniques essential for training effective models. Finally, it highlights the unique features of Rust that make it an ideal language for implementing machine learning solutions, providing practical examples that illustrate how to leverage Rust’s strengths in real-world applications.
1.1. Introduction to Machine Learning
Machine learning (ML) is a transformative technology that empowers computers to learn from data and make decisions or predictions without being explicitly programmed for specific tasks. At its core, machine learning is about developing algorithms that can identify patterns in data, make predictions, and improve their performance over time as they are exposed to more data. This concept has become increasingly important in various fields, from healthcare to finance, where the ability to make accurate predictions can lead to significant advancements.
Machine learning (ML) can be broadly defined as a field of study that gives computers the ability to learn from data without being explicitly programmed. According to Christopher Bishop in Pattern Recognition and Machine Learning (PRML), ML is fundamentally about developing algorithms that can identify patterns in data and make predictions or decisions based on these patterns. Yasser Abu-Mostafa, in Learning from Data, emphasizes that machine learning is about understanding the data-generating process and using this understanding to predict future data or behaviors. This fundamental notion of learning from experience is central to ML’s application in various domains, including science, industry, healthcare, and technology.
Machine learning problems are commonly categorized into three types: supervised learning, unsupervised learning, and reinforcement learning. In supervised learning, the algorithm is trained on a labeled dataset, meaning that each training example is paired with the correct output. Common supervised learning tasks include classification, where the goal is to predict a categorical label, and regression, where the goal is to predict a continuous value. Unsupervised learning involves training the model on data that is not labeled, and the goal is to discover hidden patterns or structure in the input data. Tasks like clustering and dimensionality reduction fall under this category. Finally, reinforcement learning (RL) deals with agents that interact with an environment to learn a strategy that maximizes cumulative rewards, a concept that aligns with Sutton and Barto’s ideas of RL as presented in their seminal work Reinforcement Learning: An Introduction.
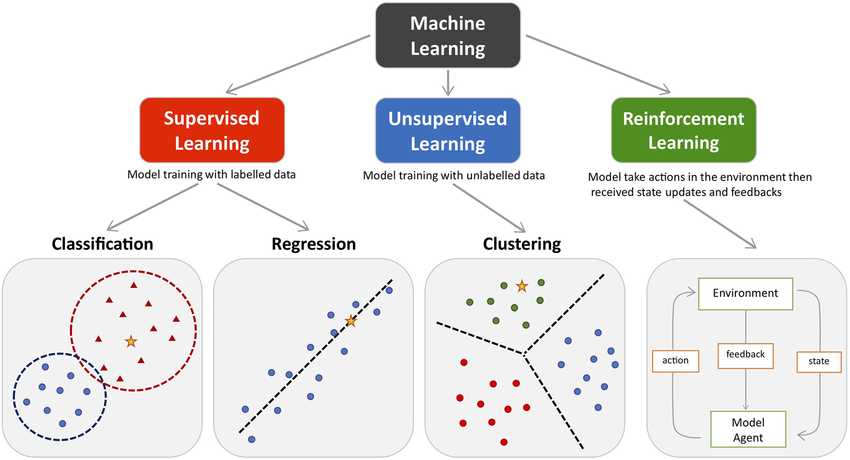
Figure 1: Major types of machine learning: supervised, unsupervised and reinforcement learning models.
The diversity of machine learning applications is vast, ranging from image and speech recognition to autonomous vehicles and medical diagnostics. Machine learning systems can recognize patterns in images to diagnose diseases, optimize supply chain processes in logistics, or forecast stock market trends based on historical data. These applications underscore the flexibility of ML models in handling various forms of structured and unstructured data, making it a powerful tool for solving complex real-world problems.
In the context of ML, the pipeline refers to the stages involved in building, training, and deploying models. The process begins with data collection, a critical step as the quality and size of the dataset significantly impact the model’s ability to generalize to new, unseen data. Data can be sourced from databases, online repositories, or real-time streams, depending on the task at hand.
Following data collection, data preprocessing is crucial for ensuring that the data is clean and ready for modeling. This involves handling missing values, encoding categorical variables, normalizing numerical features, and reducing dimensionality if necessary. According to Bishop, properly preprocessing data ensures that the model can focus on meaningful patterns rather than noise. Feature selection and feature engineering—the process of creating new features from existing ones—are also part of this phase and play an essential role in boosting model performance.
After preprocessing, the next step is modeling, where an appropriate algorithm is chosen to map inputs (features) to outputs (predictions). The algorithm could range from simple linear models to more complex neural networks. Algorithms are mathematical representations of data, and their choice depends on the nature of the problem, the type of data, and the goals of the analysis. Training the model involves optimizing its parameters to minimize prediction errors. In supervised learning, this optimization is done using techniques like gradient descent, which iteratively updates the model’s parameters to reduce the difference between the predicted and actual outputs.
Once the model is trained, evaluation measures its performance on a separate test dataset. This step ensures that the model generalizes well and avoids overfitting—where the model performs well on the training data but poorly on new data. Evaluation metrics such as accuracy, precision, recall, F1 score (for classification tasks), or RMSE (Root Mean Squared Error) for regression tasks are commonly used. Finally, the model is deployed into production environments to make real-time predictions, after which it may need to be monitored for model drift and regularly updated as new data becomes available.
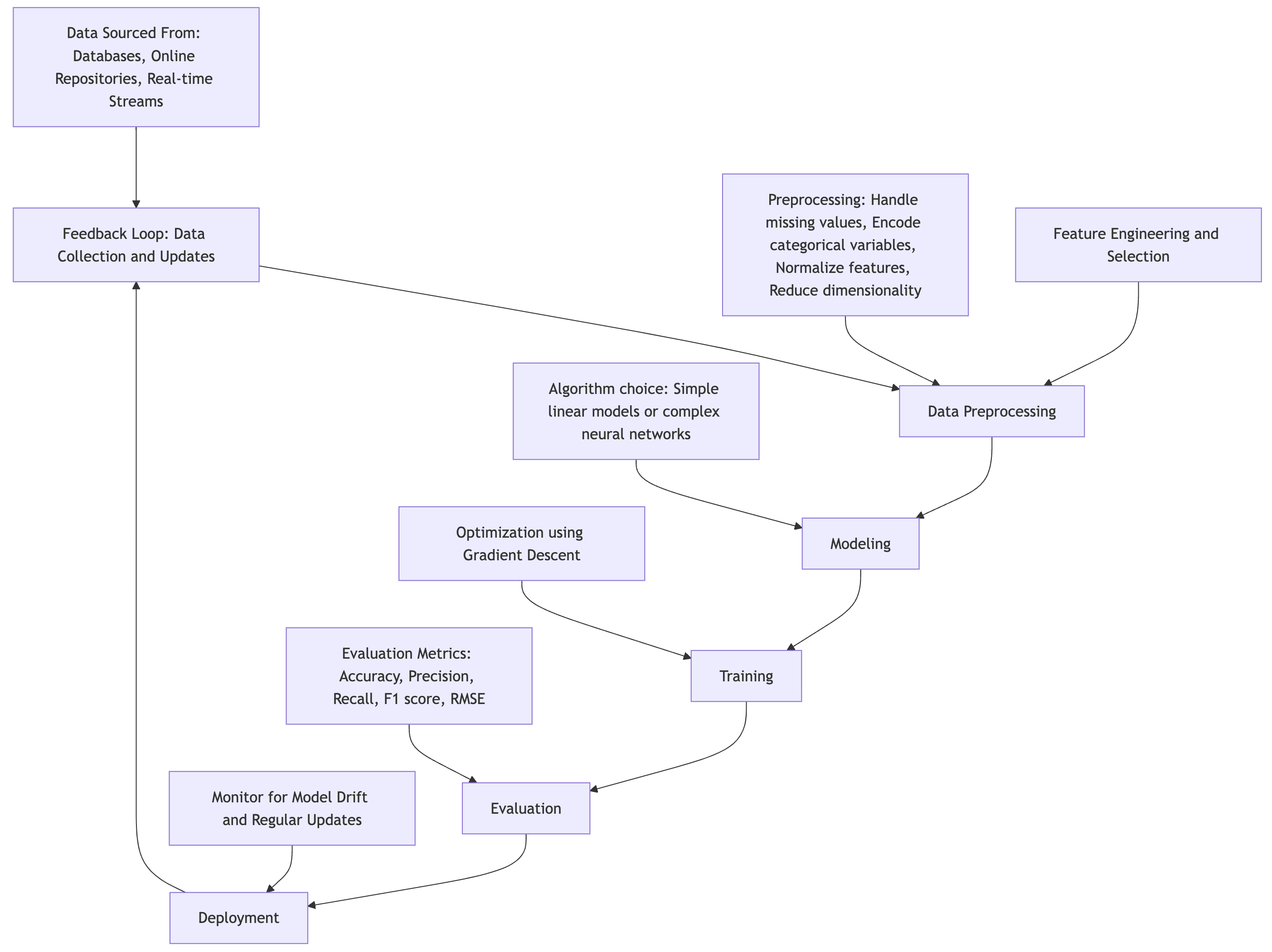
Figure 2: The main stages of the ML life cycle, starting from data collection to deployment and post-deployment monitoring.
The role of data in machine learning cannot be overstated. As Abu-Mostafa explains, "data is the fuel of machine learning," and the model's success hinges on the relevance and quality of the input data. The relationship between data, features, and the algorithm is symbiotic. Without high-quality data, even the most sophisticated algorithm will struggle to perform well. Conversely, a good understanding of the data allows for more informed decisions about which algorithms to use and how to optimize them.
Rust is a systems programming language that offers memory safety without a garbage collector, which makes it ideal for high-performance computing tasks. While Python has traditionally been the go-to language for machine learning due to its vast ecosystem of libraries (such as TensorFlow, PyTorch, and scikit-learn), Rust’s ability to deliver both performance and safety makes it increasingly relevant for machine learning, particularly in areas where performance, control, and concurrency are critical.
To start building machine learning applications in Rust, you need to set up a Rust environment, which can be done by installing Rust through the Rustup toolchain manager:
curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh
After setting up the environment, create a new Rust project using Cargo:
cargo new mlvr_project
cd mlvr_project
One of the key libraries in the Rust ecosystem for numerical computing is ndarray, which is similar to Python’s NumPy. It supports multi-dimensional arrays, which are essential for handling datasets in machine learning. You can also use the linfa crate, which provides a suite of classical machine learning algorithms such as linear regression, k-means clustering, and more.
Here’s a basic example of setting up a linear regression model using Rust, leveraging the ndarray crate to manipulate arrays and matrices:
[dependencies]
ndarray = "0.15"
ndarray-rand = "0.14"
rand = "0.8"
linfa = "0.7"
linfa-linear = "0.7"
plotters = "0.3"
In the example below, we will demonstrate how to solve a linear regression problem where the goal is to fit a straight line through a set of data points. This problem is representative of regression tasks in machine learning, where we try to predict continuous values.
use ndarray::{Array1, Array2, Axis};
use ndarray_rand::RandomExt;
use rand::distributions::Uniform;
use linfa::Dataset;
use linfa::prelude::*;
use linfa_linear::LinearRegression;
use plotters::prelude::*;
fn main() {
// Step 1: Generate synthetic data
let num_samples = 100;
let num_features = 1;
// Create random input data (X) between -1 and 1
let x: Array2<f64> = Array2::random((num_samples, num_features), Uniform::new(-1.0, 1.0));
// Define true weights and bias
let w_true = 2.0;
let b_true = 0.5;
// Generate target values y = Xw + b + noise
let noise: Array2<f64> = Array2::random((num_samples, 1), Uniform::new(-0.1, 0.1));
let y: Array1<f64> = (&x * w_true).sum_axis(Axis(1)) + b_true + noise.column(0);
// Step 2: Create a Dataset for linfa
let dataset = Dataset::new(x.clone(), y.clone());
// Step 3: Fit the linear regression model
let model = LinearRegression::default()
.fit(&dataset)
.expect("Model training failed");
// Step 4: Predict the target values
let y_pred = model.predict(dataset.records());
// Step 5: Evaluate the model performance using Root Mean Squared Error (RMSE)
let rmse = ((&y_pred - dataset.targets())
.mapv(|a| a.powi(2))
.mean()
.unwrap())
.sqrt();
println!("Root Mean Squared Error (RMSE): {:.4}", rmse);
// Step 6: Visualize the results (scatter plot of data and single regression line)
plot_results(&x, dataset.targets(), &y_pred).expect("Failed to plot results");
}
// Function to visualize the scatter plot of the data and a single regression line
fn plot_results(x: &Array2<f64>, y_true: &Array1<f64>, y_pred: &Array1<f64>) -> Result<(), Box<dyn std::error::Error>> {
let root = BitMapBackend::new("linear_regression_plot.png", (640, 480)).into_drawing_area();
root.fill(&WHITE)?;
// Create a chart with labels, grid, and caption
let mut chart = ChartBuilder::on(&root)
.caption("Linear Regression Results", ("sans-serif", 30).into_font())
.margin(20)
.x_label_area_size(30)
.y_label_area_size(30)
.build_cartesian_2d(-1.5..1.5, 0.0..3.0)?;
// Configure the grid and labels
chart.configure_mesh()
.x_desc("X Values")
.y_desc("Y Values")
.draw()?;
// Scatter plot for actual data points (red dots)
chart.draw_series(
y_true.iter().zip(x.axis_iter(Axis(0))).map(|(&y_val, x_val)| {
Circle::new((x_val[0], y_val), 3, ShapeStyle::from(&RED).filled())
}),
)?;
// Get the minimum and maximum values of x
let x_min = *x.column(0).iter().min_by(|a, b| a.partial_cmp(b).unwrap()).unwrap();
let x_max = *x.column(0).iter().max_by(|a, b| a.partial_cmp(b).unwrap()).unwrap();
// Get the corresponding predicted y values for the regression line
let y_min = y_pred[x.column(0).iter().position(|&val| val == x_min).unwrap()];
let y_max = y_pred[x.column(0).iter().position(|&val| val == x_max).unwrap()];
// Draw a single regression line (blue line)
chart.draw_series(LineSeries::new(
vec![(x_min, y_min), (x_max, y_max)],
&BLUE,
))?;
// Save the plot to file
root.present()?;
println!("Plot saved to 'linear_regression_plot.png'");
Ok(())
}
The Rust code implements a simple linear regression using synthetic data and the linfa machine learning library. It begins by generating random input data (x) and noisy target values (y) based on a linear equation with a specified weight and bias. The linfa-linear crate is used to fit a linear regression model to the data, and predictions (y_pred) are made. The model's performance is evaluated using Root Mean Squared Error (RMSE). The results are then visualized using the plotters crate, displaying a scatter plot of the actual data points and a single regression line. The regression line is drawn by finding the minimum and maximum x values, along with their corresponding predicted y values, to form the two endpoints of the line.
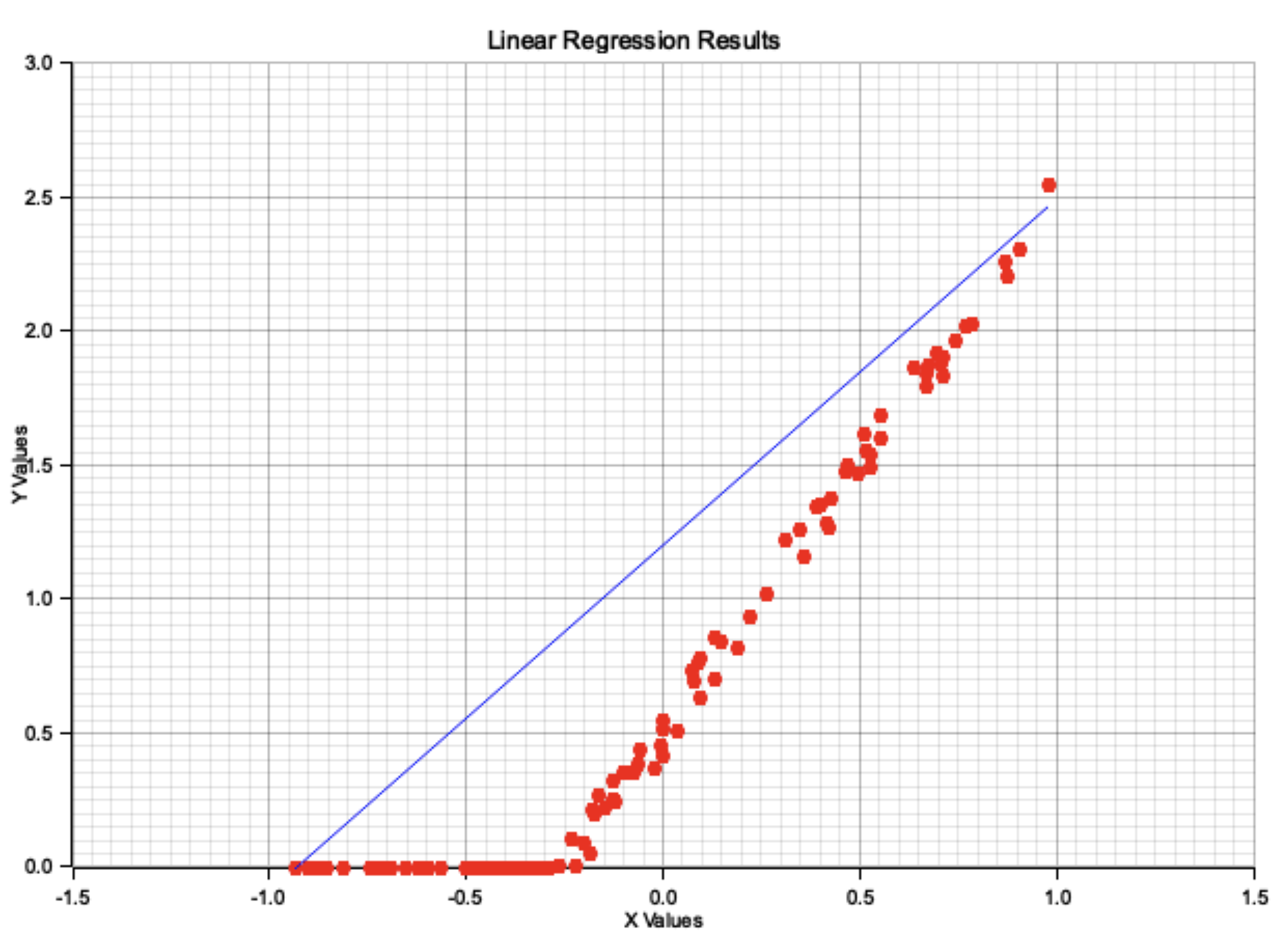
Figure 3: Linear regression result based on the previous Rust implementation code.
Lets see another example to demonstrate how to do classification on the famous Iris dataset using a decision tree classifier implemented in Rust. It starts by downloading the dataset, parsing it into features and labels, and then splitting the data into training and testing sets. A decision tree model is trained on the training set, and its performance is evaluated on the test set. The key metrics such as accuracy, precision, and recall are computed to assess the quality of the model. This example showcases how to use Rust's linfa machine learning crate to build, train, and evaluate a classifier for a real-world dataset.
[dependencies]
ndarray = "0.15"
reqwest = { version = "0.11", features = ["blocking"] }
csv = "1.1"
linfa = "0.7"
linfa-trees = "0.7"
This Rust program below performs a classification task using the Iris dataset and a decision tree classifier from the linfa_trees crate. The code begins by downloading the Iris dataset, parsing the CSV into features and labels, and then splitting it into training (70%) and testing (30%) sets.
use ndarray::{Array2, Array1, Axis, s}; // Importing `s!` macro here
use reqwest::blocking;
use std::error::Error;
use csv::ReaderBuilder;
use linfa::prelude::*;
use linfa_trees::DecisionTree;
fn download_iris_dataset(url: &str) -> Result<String, Box<dyn Error>> {
let response = blocking::get(url)?;
let dataset = response.text()?;
Ok(dataset)
}
fn parse_csv_to_ndarray(csv_data: &str) -> Result<(Array2<f64>, Array1<String>), Box<dyn Error>> {
let mut reader = ReaderBuilder::new().has_headers(true).from_reader(csv_data.as_bytes());
let mut features: Vec<Vec<f64>> = Vec::new();
let mut labels: Vec<String> = Vec::new();
for record in reader.records() {
let record = record?;
let feature_row: Vec<f64> = record.iter()
.take(4) // First four columns are features
.map(|field| field.parse::<f64>().unwrap_or(0.0)) // Parse as f64
.collect();
features.push(feature_row);
// The last column is the species label
labels.push(record[4].to_string());
}
let rows = features.len();
let cols = features[0].len();
let flat_features: Vec<f64> = features.into_iter().flatten().collect();
let features_array = Array2::from_shape_vec((rows, cols), flat_features)?;
let labels_array = Array1::from(labels);
Ok((features_array, labels_array))
}
fn print_dataset(features: &Array2<f64>, labels: &Array1<String>, dataset_name: &str) {
println!("\n{} Data:", dataset_name);
for i in 0..features.shape()[0] {
let feature_row = features.slice(s![i, ..]); // Correct usage of the `s!` macro
let label = &labels[i];
println!("Features: {:?}, Label: {}", feature_row.to_vec(), label);
}
}
fn main() -> Result<(), Box<dyn Error>> {
let url = "https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv";
// Step 1: Download the Iris dataset
let csv_data = download_iris_dataset(url)?;
println!("Downloaded Iris dataset");
// Step 2: Parse CSV data into features and labels
let (features, labels) = parse_csv_to_ndarray(&csv_data)?;
println!("Parsed dataset into ndarray");
// Step 3: Split dataset into training and testing sets (80/20 split)
let n_samples = features.shape()[0];
let split_idx = (n_samples as f64 * 0.70).round() as usize;
let (train_features, test_features) = features.view().split_at(Axis(0), split_idx);
let (train_labels, test_labels) = labels.view().split_at(Axis(0), split_idx);
// Print training and test data
print_dataset(&train_features.to_owned(), &train_labels.to_owned(), "Training");
print_dataset(&test_features.to_owned(), &test_labels.to_owned(), "Testing");
// Step 4: Fit a Decision Tree classifier using linfa
let dataset = Dataset::new(train_features.to_owned(), train_labels.to_owned());
let model = DecisionTree::params()
.max_depth(Some(5)) // Limiting the depth
.fit(&dataset)?;
println!("Trained Decision Tree model");
// Step 5: Evaluate the model on the test set
let test_dataset = Dataset::new(test_features.to_owned(), test_labels.to_owned());
let prediction = model.predict(&test_dataset);
// Step 6: Compute and print accuracy
let confusion_matrix = prediction.confusion_matrix(&test_dataset)?;
// Step 7: Compute recall, precision, accuracy
let recall = confusion_matrix.recall();
println!("Recall: {:.2}%", recall * 100.0);
let precision = confusion_matrix.precision();
println!("Precision: {:.2}%", precision * 100.0);
let accuracy = confusion_matrix.accuracy();
println!("Accuracy: {:.2}%", accuracy * 100.0);
Ok(())
}
After printing the training and test datasets, the program fits a decision tree classifier with a maximum depth of 5 on the training data. The model is then evaluated on the test data, and performance metrics such as recall, precision, and accuracy are calculated using the confusion matrix. The given program provides a complete workflow for training and evaluating a simple decision tree model for classification in Rust.
The strength of Rust lies not only in its performance but also in its concurrency and safety guarantees. Rust’s ownership system ensures that machine learning applications can be developed in a highly efficient way without worrying about common issues like memory leaks or race conditions, which can be prevalent in multi-threaded environments. This is especially beneficial for machine learning workloads that require parallel data processing or model training across multiple threads or distributed systems.
Rust’s growing ecosystem for machine learning includes libraries like tch-rs, which provides Rust bindings to PyTorch, allowing developers to leverage PyTorch's deep learning capabilities while maintaining Rust’s safety and performance. Additionally, Rust can seamlessly integrate with GPU computation through libraries like cuda-sys for advanced ML tasks, such as training deep neural networks, where GPU acceleration is often crucial for performance.
The field of machine learning is deeply rooted in both theoretical and practical understanding of data and algorithms. While Python has historically been the dominant language in machine learning, Rust is emerging as a powerful alternative due to its memory safety, performance, and concurrency capabilities. By leveraging crates such as ndarray, linfa, and tch-rs, Rust can handle a wide variety of machine learning tasks, from simple linear regression models to complex neural networks.
In summary, we have introduced the foundational concepts of machine learning, explained the machine learning pipeline, and demonstrated practical examples of implementing ML algorithms using Rust. As machine learning continues to evolve, so too will the tools and techniques that power it, and Rust's promise of safe, high-performance code positions it well as a contender in this space.
1.2. Defining the Machine Learning Problem
At its core, supervised machine learning model can be understood as a function approximation problem. Given a dataset consisting of input features $X \in \mathbb{R}^d$ and corresponding target outputs $Y \in \mathbb{R}$, the goal of a learning algorithm is to find a function $f: \mathbb{R}^d \to \mathbb{R}$ that maps inputs to outputs as accurately as possible. Formally, this can be written as:
$$f(X) = Y$$
However, in practice, the true function that governs the relationship between $X$ and $Y$ is unknown. What we observe are pairs of data $(x_i, y_i)$ drawn from an underlying (and typically unknown) joint probability distribution $P(X, Y)$. The goal of supervised machine learning is to approximate the true function $f^*(X)$ from this data.
This gives rise to a key distinction between the problem statement and the algorithmic solution. The problem statement refers to what needs to be predicted, i.e., identifying the output $Y$ given input $X$. The algorithmic solution refers to how this prediction is made, which involves selecting a model (or hypothesis) and using an algorithm to optimize this model's performance based on the data.
In classical approaches, problems are often solved using deterministic algorithms that do not rely on data but instead use predefined rules. In contrast, machine learning leverages data to "learn" these rules, making it a probabilistic approach. The learning-based approach is particularly advantageous when dealing with complex problems where deterministic methods are not feasible due to the lack of explicit knowledge about the underlying system.
In machine learning, the formulation of a problem is inherently data-driven. This means that the structure of the problem and the assumptions about the data must be carefully considered. For example, one common assumption in many learning problems is linearity, where the relationship between $X$ and $Y$ is assumed to be linear. However, this assumption may not always hold, and recognizing when non-linear models are needed is crucial. Another critical assumption is the independence of data points, which allows us to treat observations as being independently drawn from the same distribution. These assumptions play a central role in determining the appropriateness of the chosen model and the expected generalization performance.
The process of defining a supervised machine learning problem begins with identifying the input features $X$ and the target outputs $Y$. These inputs are often vectors, where each element represents a different feature of the data (e.g., age, height, or temperature), and the output can either be a scalar or a vector, depending on whether we are dealing with a single prediction or multiple predictions.
The next conceptual step is to determine the type of learning problem. Machine learning problems are typically categorized as either supervised, unsupervised, or reinforcement learning. In supervised learning, the input-output pairs $(x_i, y_i)$ are provided to the algorithm, and the goal is to learn a mapping that can predict future $y$-values for unseen $x$-values. In unsupervised learning, the algorithm only receives the inputs $x_i$ without corresponding outputs and must learn the underlying structure in the data. Reinforcement learning, on the other hand, involves learning a policy that maximizes long-term rewards in a dynamic environment by interacting with it.
Once the inputs and outputs are identified, we define the task as either a regression or classification problem. In a regression problem, the target variable $Y$ is continuous, and the goal is to predict values within a continuous range. In a classification problem, the target variable is categorical, and the aim is to assign inputs to one of a discrete set of classes.
The next important step in defining a machine learning problem is to specify the objective function, which quantifies how well the model is performing. For classification tasks, popular objective functions include the cross-entropy loss, which is used for multi-class classification, and the hinge loss, used in support vector machines. For regression, common objective functions include the mean squared error (MSE) and the mean absolute error (MAE), which measure the average deviation between the predicted and actual values. These loss functions are critical in driving the optimization process during model training.
Choosing the correct hypothesis class for the problem is essential. The hypothesis class refers to the set of models that the learning algorithm is allowed to choose from. For example, in linear regression, the hypothesis class consists of all possible linear functions. In contrast, for a neural network, the hypothesis class includes a much broader range of non-linear functions. The selection of the hypothesis class is a balance between expressiveness and tractability; overly complex models may lead to overfitting, where the model performs well on the training data but poorly on unseen data, while too simple models may underfit, failing to capture important patterns in the data.
Generalization, the ability of a model to perform well on unseen data, is a central concern in machine learning. Overfitting is mitigated by various techniques, such as cross-validation, regularization (e.g., L1 or L2 regularization), and dropout for neural networks. These techniques aim to ensure that the model captures the underlying signal rather than the noise in the training data.
Another important part of problem definition is preprocessing the input data, which includes steps like feature scaling and normalization. Feature scaling ensures that all input features are on the same scale, which is crucial when using algorithms that rely on distance metrics, such as support vector machines and k-nearest neighbors. Normalization adjusts the data so that it has a mean of zero and a standard deviation of one, improving convergence during optimization.
Handling missing data is also essential. Missing data can be addressed by removing incomplete samples or using imputation techniques, such as filling missing values with the mean, median, or mode of the feature, or more sophisticated methods like k-nearest neighbors imputation.
Finally, a well-defined machine learning problem must consider model complexity and the bias-variance tradeoff. A more complex model is more likely to have low bias but high variance, meaning it can capture complex patterns in the data but may overfit. Conversely, a simpler model may have higher bias and lower variance, leading to underfitting but better generalization. The key is to find a balance between these two extremes, which can be achieved through careful selection of the model, regularization, and proper validation techniques.
In summary, the definition of a machine learning problem is a multi-faceted process involving both mathematical rigor and conceptual understanding. It requires careful consideration of the data, assumptions, task type, and the interplay between model complexity and generalization. By grounding these ideas in mathematical principles and aligning them with the concepts found in Pattern Recognition and Machine Learning and Learning from Data, we establish a foundation for systematically addressing machine learning challenges.
1.3. Data and Feature Representation
Data in machine learning is broadly classified into structured and unstructured formats. Structured data is organized in a tabular format, where each row represents an observation and each column represents a feature. Examples include numerical data (e.g., age, height, salary) and categorical data (e.g., gender, country, occupation). These types of data are easily stored in relational databases or spreadsheets, making them well-suited for classical machine learning algorithms that expect a fixed input-output structure. Mathematically, structured data can be represented as a matrix $X \in \mathbb{R}^{n \times d}$, where $n$ is the number of samples and $d$ is the number of features.
On the other hand, unstructured data lacks a predefined format or structure and includes types such as text, images, and audio. Unstructured data often requires specialized techniques for feature extraction, such as natural language processing (NLP) for text data or convolutional neural networks (CNNs) for image data. While structured data fits neatly into the matrix representation, unstructured data must be transformed into a structured format before it can be fed into machine learning models. For example, text data is often represented using techniques like TF-IDF or word embeddings, which map words to high-dimensional numerical vectors.
In machine learning, features are the variables used by the model to make predictions. These features can be numerical, categorical, or more complex, such as text or images. Numerical features are continuous variables, such as height, weight, or price, and are represented mathematically as real numbers $x_i \in \mathbb{R}$. Categorical features represent discrete groups or categories, such as gender or product type. These features are often encoded as integers (e.g., $\{0, 1\}$ for binary categories or $\{0, 1, \dots, k-1\}$ for multi-class categories) or using one-hot encoding.
Text and image data are more complex types of features. In the case of text, each document or sentence is tokenized into words or subwords, and these tokens are transformed into numerical representations through techniques like Bag-of-Words, TF-IDF (Term Frequency-Inverse Document Frequency), or word embeddings (e.g., Word2Vec, GloVe). Images, which are represented as matrices of pixel values, require additional preprocessing steps such as resizing, normalization, and augmentation. The features from images are typically extracted using convolutional neural networks that capture spatial relationships within the data.
One of the most crucial stages in machine learning is data preprocessing, which involves transforming raw data into a form suitable for modeling. Feature engineering, a key aspect of this process, includes creating new features from existing data, transforming features into formats that can be better understood by machine learning models, and handling missing data. Poor data representation can lead to suboptimal model performance, while well-engineered features can significantly improve accuracy and generalization.
Data normalization, for instance, is essential when dealing with numerical data that have different ranges. Without normalization, features with larger ranges might disproportionately affect the learning algorithm, especially in models that rely on distance metrics, such as k-nearest neighbors or support vector machines. Mathematically, normalization involves transforming the data such that each feature has a mean of zero and a standard deviation of one. If $X = \{x_1, x_2, \dots, x_n\}$ represents a feature vector, normalization can be expressed as:
$$\hat{x}_i = \frac{x_i - \mu}{\sigma}$$
where $\mu$ is the mean of the feature and $\sigma$ is the standard deviation. This transformation ensures that all features contribute equally to the learning process, improving convergence and model stability.
Encoding categorical variables is another essential preprocessing step. In some cases, categorical variables can be transformed into numerical values using label encoding, where each category is mapped to a unique integer. However, this approach can introduce unintended ordinal relationships between categories, leading to poor performance in algorithms that assume numerical relationships between features. A better approach is one-hot encoding, where each category is represented by a binary vector. For example, if the feature "color" has three categories $\{\text{red}, \text{green}, \text{blue}\}$, one-hot encoding would represent "red" as $[1,0,0]$, "green" as $[0, 1, 0]$, and "blue" as $[0, 0, 1]$.
Handling missing data is equally important. Missing data can distort statistical relationships, bias results, and reduce the predictive power of a model. Common strategies to handle missing data include imputing missing values with the mean, median, or mode of the feature, using more sophisticated techniques such as k-nearest neighbors imputation, or removing incomplete records altogether. The choice of strategy depends on the nature of the data and the proportion of missing values.
Rust, known for its safety, performance, and concurrency, provides a powerful platform for data manipulation. In the context of machine learning, the serde and ndarray crates are essential for handling structured data, while other crates can be used for advanced tasks like feature extraction and transformation.
The serde crate provides mechanisms for serializing and deserializing data, which is critical for loading and saving datasets in formats such as CSV, JSON, and binary. For example, we can easily load a CSV file containing structured data and convert it into Rust’s native data structures.
use serde::Deserialize;
use std::error::Error;
use std::fs::File;
use std::io::Read;
#[derive(Debug, Deserialize)]
struct Record {
age: Option<f64>,
height: Option<f64>,
gender: Option<String>,
}
fn load_data_from_csv(path: &str) -> Result<Vec<Record>, Box<dyn Error>> {
let file = File::open(path)?;
let mut rdr = csv::Reader::from_reader(file);
let mut records = Vec::new();
for result in rdr.deserialize() {
let record: Record = result?;
records.push(record);
}
Ok(records)
}
For numerical data manipulation, the ndarray crate is ideal for working with multidimensional arrays and matrices, which are common representations in machine learning. Feature extraction and transformation often involve manipulating numerical arrays. For example, applying normalization to a dataset can be easily implemented using ndarray:
use ndarray::Array2;
fn normalize_features(mut data: Array2<f64>) -> Array2<f64> {
let axis = ndarray::Axis(0); // Normalize across columns (features)
let mean = data.mean_axis(axis).unwrap();
let std_dev = data.std_axis(axis, 0.0);
for mut row in data.rows_mut() {
for (i, elem) in row.iter_mut().enumerate() {
*elem = (*elem - mean[i]) / std_dev[i];
}
}
data
}
The code normalizes each feature in the dataset by subtracting the mean and dividing by the standard deviation. The normalized dataset is now ready for machine learning algorithms that require features to be on the same scale.
In addition to normalization, encoding categorical variables and handling missing data can also be efficiently implemented in Rust. For example, we can use the Option type in Rust to represent missing data, and later apply imputation strategies to fill in the gaps.
Let’s see a code demonstration on how to download the Titanic dataset from a public URL, preprocess the data for machine learning, and prepare it for ML classification tasks. The program first fetches the dataset using the reqwest crate, parses the CSV data into a numerical format using csv and ndarray, and then performs a series of preprocessing steps such as normalization of numerical features. Use the following for cargo.toml file.
[dependencies]
reqwest = { version = "0.11", features = ["blocking"] }
csv = "1.1"
ndarray = "0.15"
ndarray-rand = "0.14"
rand = "0.8.5"
The code below includes functionality for splitting the dataset into training and testing sets, allowing users to evaluate the quality of the data by checking for missing values (NaN).
use csv::ReaderBuilder;
use linfa::prelude::*;
use linfa_svm::SvmParams;
use ndarray::Array1;
use ndarray::Array2;
use ndarray::ArrayBase;
use ndarray::Axis;
use ndarray::Dim;
use ndarray::OwnedRepr;
use rand::seq::SliceRandom;
use reqwest::blocking::get;
use std::collections::HashMap;
use std::error::Error;
use std::io::Cursor;
// Function to download Titanic dataset
fn download_titanic_data() -> Result<String, Box<dyn Error>> {
let url = "https://raw.githubusercontent.com/datasciencedojo/datasets/master/titanic.csv";
let response = get(url)?.text()?;
Ok(response)
}
// Function to load Titanic data into ndarray
fn load_titanic_to_ndarray(data: &str) -> Result<(Vec<String>, Array2<f64>), Box<dyn Error>> {
let mut reader = ReaderBuilder::new().from_reader(Cursor::new(data));
// Get the headers (metadata)
let headers: Vec<String> = reader.headers()?.iter().map(|s| s.to_string()).collect();
// Store column indices for categorical columns
let categorical_columns = vec!["Sex", "Embarked"]; // Example categorical columns
let mut cat_col_indices: HashMap<String, usize> = HashMap::new();
for (i, header) in headers.iter().enumerate() {
if categorical_columns.contains(&header.as_str()) {
cat_col_indices.insert(header.clone(), i);
}
}
// Extract records and convert to f64 ndarray with one-hot encoding for categorical columns
let mut records = Vec::new();
let mut one_hot_data = Vec::new();
for result in reader.records() {
let record = result?;
let mut row = vec![0.0; headers.len()];
for (i, field) in record.iter().enumerate() {
if let Some(cat_index) = cat_col_indices.get(&headers[i]) {
// Handle categorical columns with one-hot encoding
let encoded = match &headers[*cat_index].as_str() {
&"Sex" => match field {
"male" => vec![1.0, 0.0], // Male
"female" => vec![0.0, 1.0], // Female
_ => vec![0.0, 0.0], // Unknown
},
&"Embarked" => match field {
"C" => vec![1.0, 0.0, 0.0], // Cherbourg
"Q" => vec![0.0, 1.0, 0.0], // Queenstown
"S" => vec![0.0, 0.0, 1.0], // Southampton
_ => vec![0.0, 0.0, 0.0], // Unknown
},
_ => vec![0.0], // Just in case
};
one_hot_data.push(encoded);
} else {
// Handle numerical columns
row[i] = field.parse::<f64>().unwrap_or(f64::NAN);
}
}
records.push(row);
}
// Flatten one-hot encoded columns and append to records
let one_hot_flattened: Vec<f64> = one_hot_data.into_iter().flatten().collect();
let num_rows = records.len();
let num_cat_cols = one_hot_flattened.len() / num_rows;
let mut expanded_records = records
.into_iter()
.map(|mut row| {
row.extend(vec![0.0; num_cat_cols]);
row
})
.collect::<Vec<Vec<f64>>>();
for (i, record) in expanded_records.iter_mut().enumerate() {
let cat_data_start = i * num_cat_cols;
record.splice(
headers.len()..headers.len() + num_cat_cols,
one_hot_flattened[cat_data_start..cat_data_start + num_cat_cols].to_vec(),
);
}
// Create an ndarray from the CSV records
let flat_data: Vec<f64> = expanded_records.into_iter().flatten().collect();
let array = Array2::from_shape_vec((num_rows, headers.len() + num_cat_cols), flat_data)?;
Ok((headers, array))
}
// Function to print the top rows of the data
fn print_top_rows(data: &Array2<f64>, num_rows: usize) {
println!("First {} rows of the data:", num_rows);
for row in data.rows().into_iter().take(num_rows) {
println!("{:?}", row);
}
}
// Function to preprocess data: remove rows with NaN and normalize
fn preprocess_data(data: &mut Array2<f64>, numerical_columns: &[usize]) {
// Remove rows with NaN values in numerical columns
let mask: Vec<bool> = data
.rows()
.into_iter()
.map(|row| numerical_columns.iter().all(|&col| !row[col].is_nan()))
.collect();
let filtered_data: Array2<f64> = data.select(
Axis(0),
&mask
.iter()
.enumerate()
.filter_map(|(i, &keep)| if keep { Some(i) } else { None })
.collect::<Vec<usize>>(),
);
// Normalize only the specified numerical columns
let mut normalized_data = filtered_data.to_owned();
for &col in numerical_columns {
// Extract the column
let column = filtered_data.column(col);
let mean = column.mean().unwrap_or(0.0);
let std_dev = column.std(0.0);
// Normalize the column
for elem in normalized_data.column_mut(col) {
*elem = (*elem - mean) / std_dev;
}
}
*data = normalized_data;
println!("Data has been preprocessed: NaN values removed and features normalized.");
}
// Function to split data into training and testing sets
fn split_data(data: &Array2<f64>, train_size: f64) -> (Array2<f64>, Array2<f64>) {
let total_rows = data.shape()[0];
let split_index = (total_rows as f64 * train_size).round() as usize;
let shuffled_indices: Vec<usize> = (0..total_rows)
.collect::<Vec<usize>>()
.choose_multiple(&mut rand::thread_rng(), total_rows)
.cloned()
.collect();
let train_data = data.select(Axis(0), &shuffled_indices[0..split_index]);
let test_data = data.select(Axis(0), &shuffled_indices[split_index..]);
(train_data, test_data)
}
fn main() -> Result<(), Box<dyn Error>> {
// Step 1: Download Titanic dataset
let raw_data = download_titanic_data()?;
// Step 2: Load Titanic data into ndarray
let (_headers, titanic_data) = load_titanic_to_ndarray(&raw_data)?;
let mut titanic_data = titanic_data.select(Axis(1), &[1, 2, 4, 5, 6, 7, 9, 11]); // Example: selecting a few numerical features
// Step 3: Preprocess the data
preprocess_data(&mut titanic_data, &[3, 4, 5, 6]);
// Step 4: Define features and labels for classification (survival prediction)
let labels = titanic_data.column(0).to_owned(); // Assuming the 'Survived' column is at index 1
let labels = labels.clone().into_shape((labels.len(), 1))?;
let features = titanic_data.select(Axis(1), &[1, 2, 3, 4, 5, 6, 7]); // Example: selecting a few numerical features
// Step 5: Split data into training and testing sets
let (train_features, test_features) = split_data(&features, 0.8);
let (train_labels, test_labels) =
split_data(&labels.clone().into_shape((labels.len(), 1))?, 0.8); // Cloning labels to avoid moving
let train_labels = train_labels.iter().cloned().collect::<Array1<f64>>();
let test_labels = test_labels.iter().cloned().collect::<Array1<f64>>();
println!("Data has been split into training and testing datasets.");
// Step 6: Show top rows
print_top_rows(&train_features, 10);
// Step 7: Evaluate the quality of the data
println!("Checking for NaN values in training data...");
let num_nan_train: usize = train_features.iter().filter(|&&x| x.is_nan()).count();
let num_nan_test: usize = test_features.iter().filter(|&&x| x.is_nan()).count();
println!("Number of NaN values in training data: {}", num_nan_train);
println!("Number of NaN values in test data: {}", num_nan_test);
Ok(())
}
The code begins by downloading and parsing the Titanic dataset into an ndarray structure, which facilitates efficient matrix operations in Rust. Categorical columns such as "Sex" and "Embarked" are one-hot encoded to convert them into a numerical format, ensuring the dataset is suitable for numerical processing. The preprocessing step removes rows with NaN values in specified numerical columns (e.g., Age, SibSp, Parch, Fare) and normalizes these features by adjusting their mean and standard deviation for consistency. After selecting relevant features and defining the target label (Survived), the dataset is shuffled and split into training and testing sets, preparing it for machine learning tasks. Finally, the code checks for any remaining NaN values in both the training and testing sets, addressing potential issues that could affect model performance.
Handling NaN (Not a Number) values in a dataset is a crucial step in data preprocessing as these missing values can lead to errors or degrade the performance of machine learning models. Common strategies to handle NaN values include imputation or removal. In imputation, missing values are filled with statistical measures like the mean, median, or mode of the respective feature, or more advanced methods like K-nearest neighbors (KNN) or regression models can be used to estimate the missing values. If the proportion of missing values is small, it may be preferable to remove rows or columns containing NaNs. Another option is to use forward or backward filling for time series data, where missing values are filled based on adjacent data points. The method chosen should depend on the nature of the data and the importance of the missing information.
In conclusion, understanding data and feature representation is a critical starting point of machine learning. Whether dealing with structured or unstructured data, preprocessing steps like normalization, encoding, and handling missing data are essential for building effective models. Rust provides powerful tools for performing these operations, ensuring that data manipulation is safe, efficient, and concurrent. By leveraging the features of Rust, we can implement robust machine learning pipelines that transform raw data into meaningful representations for modeling.
1.4. Model Selection and Evaluation
Model selection and evaluation are critical steps in the machine learning pipeline. The choice of the model significantly impacts the performance and accuracy of the predictions made by the system. Selecting the right model involves understanding the problem at hand and choosing an appropriate algorithm that can solve it effectively. This section explores the fundamental concepts of model types, the challenges of overfitting and underfitting, criteria for model selection, and practical methods for evaluating models in Rust.
There are several types of models in machine learning, each designed to solve different kinds of problems. Regression models are used when the task involves predicting continuous values, such as predicting house prices or stock market trends. Classification models, on the other hand, are used to predict discrete labels, such as determining whether an email is spam or not. Clustering models are unsupervised models used to group data into clusters based on similarity, such as customer segmentation in marketing. Understanding the nature of the problem is the first step in selecting an appropriate model.
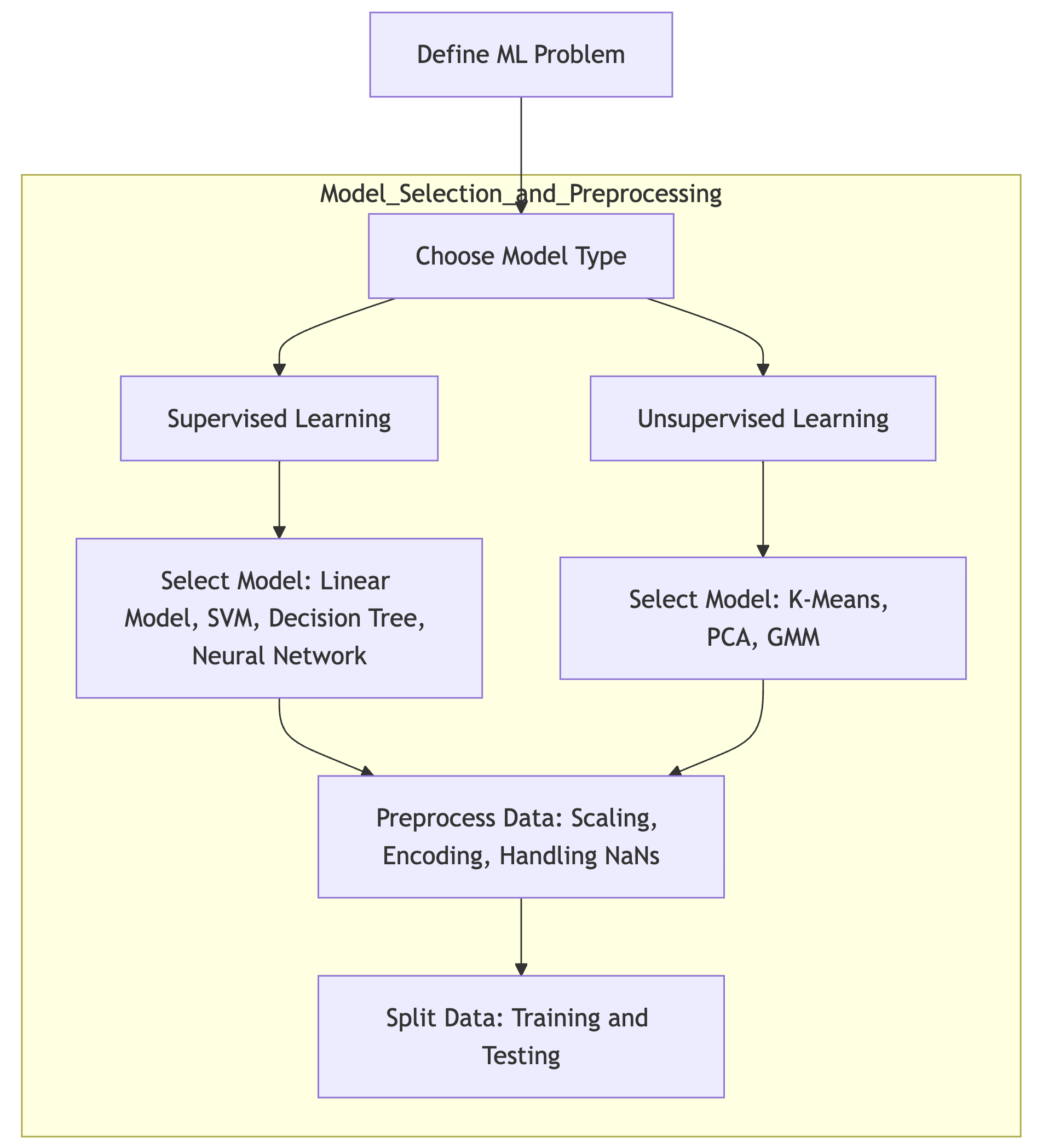
Figure 4: Model selection and preprocessing steps.
Supervised learning models are essential in predicting outcomes based on labeled data. In the case of regression problems, models like linear regression predict continuous variables by finding a function $f(x)$ that minimizes the error between predicted and actual outputs, typically through a least squares method. Classification tasks involve assigning labels to discrete categories, with models like logistic regression, decision trees, random forests, and support vector machines (SVMs). Decision trees recursively split the data on feature values to form a tree-like structure, while random forests enhance performance by averaging the outputs of multiple trees to reduce variance. SVMs, on the other hand, maximize the margin between classes using linear or non-linear kernels such as the Radial Basis Function (RBF). Neural networks are highly flexible models capable of capturing non-linear relationships through a system of interconnected nodes, using techniques like backpropagation to minimize the error. Each model offers different trade-offs in terms of complexity, interpretability, and accuracy, which are critical factors in the model selection process.
In contrast to supervised learning, unsupervised learning models are designed to uncover hidden structures in data without labeled outputs. Clustering models, such as k-means, aim to partition the dataset into distinct groups based on similarity measures, often using Euclidean distance. Dimensionality reduction models, such as Principal Component Analysis (PCA) and t-SNE, reduce the number of features in the data while retaining as much variance as possible, helping in visualizing high-dimensional data or speeding up computations in downstream tasks. Another important category is density estimation, where models such as Gaussian Mixture Models (GMM) estimate the underlying probability distribution of the data, providing insights into the data's structure and enabling anomaly detection. The choice of model in unsupervised learning depends heavily on the goals of the task, whether it be for clustering, visualization, or anomaly detection.
A central challenge in model selection is balancing overfitting and underfitting. Overfitting occurs when a model learns not only the underlying patterns in the training data but also the noise and random fluctuations, resulting in poor generalization to unseen data. Mathematically, overfitting can be understood as a situation where the hypothesis class is too complex, leading to a high variance in model predictions across different datasets. In contrast, underfitting occurs when the model is too simple and fails to capture the underlying structure, resulting in high bias and poor performance on both training and test data. These two concepts form the basis of the bias-variance tradeoff: increasing model complexity reduces bias but increases variance, while simplifying the model decreases variance but increases bias. The objective is to find a model with an optimal balance, ensuring that the model generalizes well beyond the training dataset.
The process of selecting a machine learning model involves evaluating a series of criteria, including model complexity, training time, interpretability, and expected performance on unseen data. One widely accepted framework is the use of cross-validation, where the dataset is split into several folds, with each fold taking turns as the test set while the others serve as the training set. This approach provides a robust estimate of the model's performance and reduces the risk of overfitting. A specific type of cross-validation is k-fold cross-validation, where the dataset is split into $k$ equally sized folds, and the model is trained $k$ times, with each fold being used once as the test set. The performance metrics are then averaged across all $k$ trials to obtain a more reliable estimate of the model’s generalization capabilities.

Figure 5: Training evaluation and final selection.
Another key consideration in model selection is the bias-variance tradeoff, as discussed earlier. By incorporating regularization techniques, such as L1 (lasso) or L2 (ridge) regularization, we can penalize large coefficients in linear models, reducing the risk of overfitting while preserving model flexibility. Automatic model selection frameworks like AutoML aim to automate the process of model selection and hyperparameter tuning by evaluating various models and configurations using cross-validation and optimization techniques. AutoML leverages performance metrics such as accuracy for classification or mean squared error for regression to determine the best model configuration.
Evaluating the performance of a model is essential to ensure that it meets the desired criteria. Various metrics can be used depending on the type of problem being solved. For classification tasks, metrics such as accuracy, precision, recall, and F1 score are commonly used. Accuracy measures the overall correctness of the model, while precision measures the proportion of positive predictions that are actually correct. Recall measures the proportion of actual positives that are correctly identified, and the F1 score provides a harmonic mean of precision and recall, offering a balanced measure in cases of imbalanced datasets.
In practice, model evaluation requires the implementation of various performance metrics, which can be done efficiently in Rust using libraries like ndarray for matrix operations. Accuracy measures the overall correctness of the model's predictions, defined as:
$$ \text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}} $$
where TP, TN, FP, and FN refer to true positives, true negatives, false positives, and false negatives, respectively. Precision focuses on the proportion of correct positive predictions, while recall evaluates the model's ability to capture all positive instances. The F1 score, which is the harmonic mean of precision and recall, is useful when dealing with imbalanced datasets where one class dominates the predictions.
In Rust, implementing these evaluation metrics can be done using basic Rust syntax and libraries like ndarray for numerical operations. Below is an example of how to implement accuracy, precision, recall, and F1 score in Rust:
fn accuracy(
predictions: &ArrayBase<OwnedRepr<f64>, Dim<[usize; 1]>>,
labels: &ArrayBase<OwnedRepr<f64>, Dim<[usize; 1]>>,
) -> f64 {
let predictions_slice: Vec<f64> = predictions.iter().cloned().collect();
let labels_slice: Vec<f64> = labels.iter().cloned().collect();
let correct = predictions_slice
.iter()
.zip(labels_slice.iter())
.filter(|&(p, l)| p == l)
.count();
correct as f64 / predictions.len() as f64
}
fn precision(
predictions: &ArrayBase<OwnedRepr<f64>, Dim<[usize; 1]>>,
labels: &ArrayBase<OwnedRepr<f64>, Dim<[usize; 1]>>,
) -> f64 {
let predictions_slice: Vec<f64> = predictions.iter().cloned().collect();
let labels_slice: Vec<f64> = labels.iter().cloned().collect();
let true_positive = predictions_slice
.iter()
.zip(labels_slice.iter())
.filter(|&(p, l)| *p == 1.0 && *l == 1.0)
.count();
let predicted_positive = predictions_slice.iter().filter(|&&p| p == 1.0).count();
if predicted_positive == 0 {
return 0.0; // No positive predictions, return 0 precision
}
true_positive as f64 / predicted_positive as f64
}
fn recall(
predictions: &ArrayBase<OwnedRepr<f64>, Dim<[usize; 1]>>,
labels: &ArrayBase<OwnedRepr<f64>, Dim<[usize; 1]>>,
) -> f64 {
let predictions_slice: Vec<f64> = predictions.iter().cloned().collect();
let labels_slice: Vec<f64> = labels.iter().cloned().collect();
let true_positive = predictions_slice
.iter()
.zip(labels_slice.iter())
.filter(|&(p, l)| *p == 1.0 && *l == 1.0)
.count();
let actual_positive = labels_slice.iter().filter(|&&l| l == 1.0).count();
true_positive as f64 / actual_positive as f64
}
fn f1_score(
predictions: &ArrayBase<OwnedRepr<f64>, Dim<[usize; 1]>>,
labels: &ArrayBase<OwnedRepr<f64>, Dim<[usize; 1]>>,
) -> f64 {
let p = precision(predictions, labels);
let r = recall(predictions, labels);
2.0 * (p * r) / (p + r)
}
// Function to train an SVM and get predictions
fn train_and_predict_svm(
train_features: &Array2<f64>,
train_labels: &Array1<f64>,
test_features: &Array2<f64>,
) -> Result<Array1<f64>, Box<dyn Error>> {
println!("Train features shape: {:?}", train_features.shape());
println!("Train labels shape: {:?}", train_labels.shape());
println!("Test features shape: {:?}", test_features.shape());
// Convert the training data into a Linfa dataset
let dataset = Dataset::new(train_features.clone(), train_labels.clone());
// Initialize the SVM model
let model = SvmParams::default().linear_kernel();
// Create and train the SVM model
let model = model.fit(&dataset)?;
// Predict using the trained model
let predictions = model.predict(test_features);
// Print a few sample predictions
println!(
"Sample predictions: {:?}",
&predictions.map(|&x| if x < 0.5 { 0 } else { 1 })
);
// For now, we'll return predictions from the last model
Ok(predictions.map(|&x| if x < 0.5 { 0.0 } else { 1.0 }))
}
fn main() -> Result<(), Box<dyn Error>> {
// Titanic dataset loaded and cleaned
// ...
// Train SVM and get predictions
let predictions = train_and_predict_svm(&train_features, &train_labels, &test_features)?;
println!("Test Labels: {:?}", test_labels);
println!("Predictions: {:?}", predictions);
println!("Accuracy: {:.2}", accuracy(&predictions, &test_labels));
println!("Precision: {:.2}", precision(&predictions, &test_labels));
println!("Recall: {:.2}", recall(&predictions, &test_labels));
println!("F1 Score: {:.2}", f1_score(&predictions, &test_labels));
Ok(())
}
In this code, the accuracy function calculates the proportion of correct predictions by comparing the predicted labels to the actual labels. The precision function computes the ratio of true positives to the total number of predicted positives. The recall function calculates the ratio of true positives to the actual number of positives in the data. Finally, the f1_score function combines precision and recall into a single metric.
Cross-validation is another practical technique for model evaluation, and it can be implemented in Rust to ensure the model generalizes well to unseen data. A simple k-fold cross-validation can be achieved by dividing the dataset into k subsets, training the model on $k-1$ subsets, and evaluating it on the remaining subset. This process is repeated k times, and the results are averaged.
Below is an example of implementing a simple k-fold cross-validation in Rust:
use ndarray::{Array2, Axis};
use rand::seq::SliceRandom;
fn k_fold_split(data: &Array2<f64>, labels: &[u8], k: usize) -> Vec<(Array2<f64>, Vec<u8>, Array2<f64>, Vec<u8>)> {
let mut rng = rand::thread_rng();
let mut indices: Vec<usize> = (0..data.nrows()).collect();
indices.shuffle(&mut rng);
let fold_size = data.nrows() / k;
let mut folds = Vec::new();
for i in 0..k {
let start = i * fold_size;
let end = start + fold_size;
let test_indices = &indices[start..end];
let train_indices: Vec<usize> = indices.iter().cloned().filter(|&x| !test_indices.contains(&x)).collect();
let train_data = data.select(Axis(0), &train_indices);
let train_labels = train_indices.iter().map(|&i| labels[i]).collect();
let test_data = data.select(Axis(0), test_indices);
let test_labels = test_indices.iter().map(|&i| labels[i]).collect();
folds.push((train_data, train_labels, test_data, test_labels));
}
folds
}
fn main() {
// Previous code
// ...
let k = 5;
let folds = k_fold_split(&features, &labels.clone().into_shape(labels.len()).unwrap(), k);
for (i, (train_data, train_labels, test_data, test_labels)) in folds.iter().enumerate() {
println!("Fold {}: Train size = {}, Test size = {}", i + 1, train_data.nrows(), test_data.nrows());
}
}
In this example, the k_fold_split function splits the data and labels into k folds for cross-validation. It randomly shuffles the data, and then selects subsets for training and testing in each fold. The main function demonstrates how to create and print the sizes of the train and test sets for each fold. This approach is crucial for assessing the model's robustness and ensuring that it performs well across different subsets of data.
In summary, model selection and evaluation are critical steps in machine learning. Balancing between model complexity and generalization through cross-validation, understanding the bias-variance tradeoff, and applying appropriate performance metrics are essential for ensuring the selected model is well-suited for the task. Rust's capabilities, combined with the principles from Pattern Recognition and Machine Learning and Learning from Data, enable efficient and reliable model evaluation workflows.
1.5. Optimization and Training
Optimization lies at the heart of machine learning, as it directly influences the process of training models to achieve the best possible performance on a given task. In essence, optimization in machine learning involves finding the best parameters for a model such that it minimizes the loss function, which quantifies the difference between the model's predictions and the actual target values. The most widely used optimization technique in machine learning is gradient descent, which iteratively adjusts the model's parameters to minimize the loss. This section delves into the fundamental concepts of optimization, explores the role of hyperparameters, and demonstrates practical implementation in Rust.
Optimization in machine learning defined as the process of finding the optimal parameters $\theta$ for a model by minimizing or maximizing an objective function, typically a loss function. In supervised learning, the goal is often to minimize a loss function $L(\theta)$, which measures the difference between the predicted output $\hat{y} = f_\theta(x)$ and the true output $y$. Mathematically, this can be framed as an optimization problem:
$$\hat{\theta} = \arg \min_\theta L(\theta)$$
Here, $L(\theta)$ could represent various loss functions, such as mean squared error (MSE) for regression or cross-entropy for classification. The optimization process adjusts the parameters $\theta$ so that the model can make accurate predictions on unseen data.
One of the most widely used optimization algorithms in machine learning is gradient descent, which is an optimization algorithm that seeks to minimize the loss function by moving in the direction of the steepest descent. The basic idea is to compute the gradient of the loss function with respect to the model parameters and then update the parameters in the opposite direction of the gradient. The amount by which the parameters are updated is determined by the learning rate, a crucial hyperparameter that needs to be carefully tuned. A learning rate that is too high can cause the algorithm to overshoot the minimum, while a learning rate that is too low can lead to slow convergence or getting stuck in local minima.
Gradient descent iteratively updates the model parameters $\theta$ by computing the gradient of the loss function with respect to the parameters and taking steps in the direction that reduces the loss. Mathematically, this can be expressed as:
$$\theta_{t+1} = \theta_t - \eta \nabla_\theta L(\theta_t)$$
where $\eta$ is the learning rate, a hyperparameter that controls the step size in the parameter space, and $\nabla_\theta L(\theta_t)$ is the gradient of the loss function with respect to the parameters at iteration $t$. Gradient descent continues updating $\theta$ until the model converges to a minimum, defined by either a sufficiently small gradient or a lack of improvement in the loss function over successive iterations.
Beyond the basic gradient descent, there are several variants that offer improvements in convergence speed and stability. Stochastic Gradient Descent (SGD) updates the model parameters using only a single training example or a small batch at each iteration, which can make the optimization process faster and more scalable to large datasets. Other variants, like Momentum, RMSprop, and Adam, introduce additional terms that help accelerate convergence by considering the history of gradients or by adapting the learning rate for each parameter. Here is the list of several variants of gradient descent commonly used to improve convergence:
Stochastic Gradient Descent (SGD): Instead of computing the gradient over the entire dataset, SGD approximates it using a single data point or a small batch, resulting in faster updates but noisier gradients.
Mini-batch Gradient Descent: A compromise between standard gradient descent and SGD, where the gradient is computed using a subset (mini-batch) of the data at each iteration.
Momentum-based Gradient Descent: Introduces a momentum term to smooth out updates and avoid oscillations, particularly useful in optimizing non-convex functions.
Adam Optimizer: An adaptive gradient method that adjusts learning rates based on first and second moments of gradients, often used for deep learning models due to its fast convergence.
The choice of optimizer is crucial and depends on the nature of the problem, dataset size, and computational resources.
Hyperparameters, such as the learning rate $\eta$, batch size, and the number of epochs, play a significant role in the training process. The learning rate $\eta$ is one of the most critical hyperparameters; if it's too small, convergence will be slow, and if it's too large, the model may overshoot the optimal solution, failing to converge. The batch size controls the number of data points used to compute the gradient at each step, with larger batch sizes yielding more accurate gradients but requiring more memory. The number of epochs defines how many times the entire dataset is passed through the model during training.
Other hyperparameters, such as regularization parameters, will influence the model’s ability to generalize. L1 and L2 regularization terms can be added to the loss function to penalize large parameter values, thus reducing the likelihood of overfitting.
A key component of optimization is the loss function, which defines the objective of the learning algorithm. Common loss functions include the mean squared error (MSE) for regression and the cross-entropy loss for classification. The MSE loss function is given by:
$$ L(\theta) = \frac{1}{N} \sum_{i=1}^{N} (y_i - f_\theta(x_i))^2 $$
where $N$ is the number of data points, $y_i$ is the true output, and $f_\theta(x_i)$ is the predicted output for a given input $x_i$. The cross-entropy loss for classification is used to measure the dissimilarity between predicted probabilities and the true labels, defined as:
$$L(\theta) = - \sum_{i=1}^{N} y_i \log \hat{y}_i$$
where $y_i$ represents the true class labels and $\hat{y}_i$ are the predicted probabilities.
Convergence in optimization is achieved when the updates to $\theta$ become small or when the loss function stabilizes. Practically, convergence criteria can include setting a threshold for the magnitude of the gradient or the relative change in the loss over iterations. Regularization techniques like L1 (lasso) and L2 (ridge) are often used to prevent overfitting by introducing a penalty for large weights in the model. The regularized loss function for L2 regularization is:
$$ L(\theta) = \frac{1}{N} \sum_{i=1}^{N} (y_i - f_\theta(x_i))^2 + \lambda ||\theta||^2 $$
where $\lambda$ is the regularization parameter that controls the strength of the penalty.
The loss function is a key component in the optimization process, serving as a measure of how well the model's predictions match the actual targets. Common loss functions include mean squared error for regression tasks and cross-entropy loss for classification tasks. The choice of the loss function depends on the problem being solved, and it must be differentiable so that gradients can be computed. Regularization techniques, such as L1 and L2 regularization, are often employed to prevent overfitting by adding a penalty term to the loss function that discourages overly complex models.
Convergence criteria determine when the optimization process should stop. In practice, optimization is terminated when the improvement in the loss function becomes negligible, or after a predefined number of iterations (epochs). Early stopping is a popular technique where the training process is halted if the model's performance on a validation set starts to deteriorate, indicating that the model is beginning to overfit.
Training a machine learning model involves repeatedly applying the optimization algorithm to update the model's parameters. The training loop is the core of this process, where each iteration consists of computing the loss, calculating the gradients, and updating the parameters. The learning rate and other hyperparameters, such as the batch size and the number of epochs, are critical to the success of the training process and often require careful tuning through experimentation.
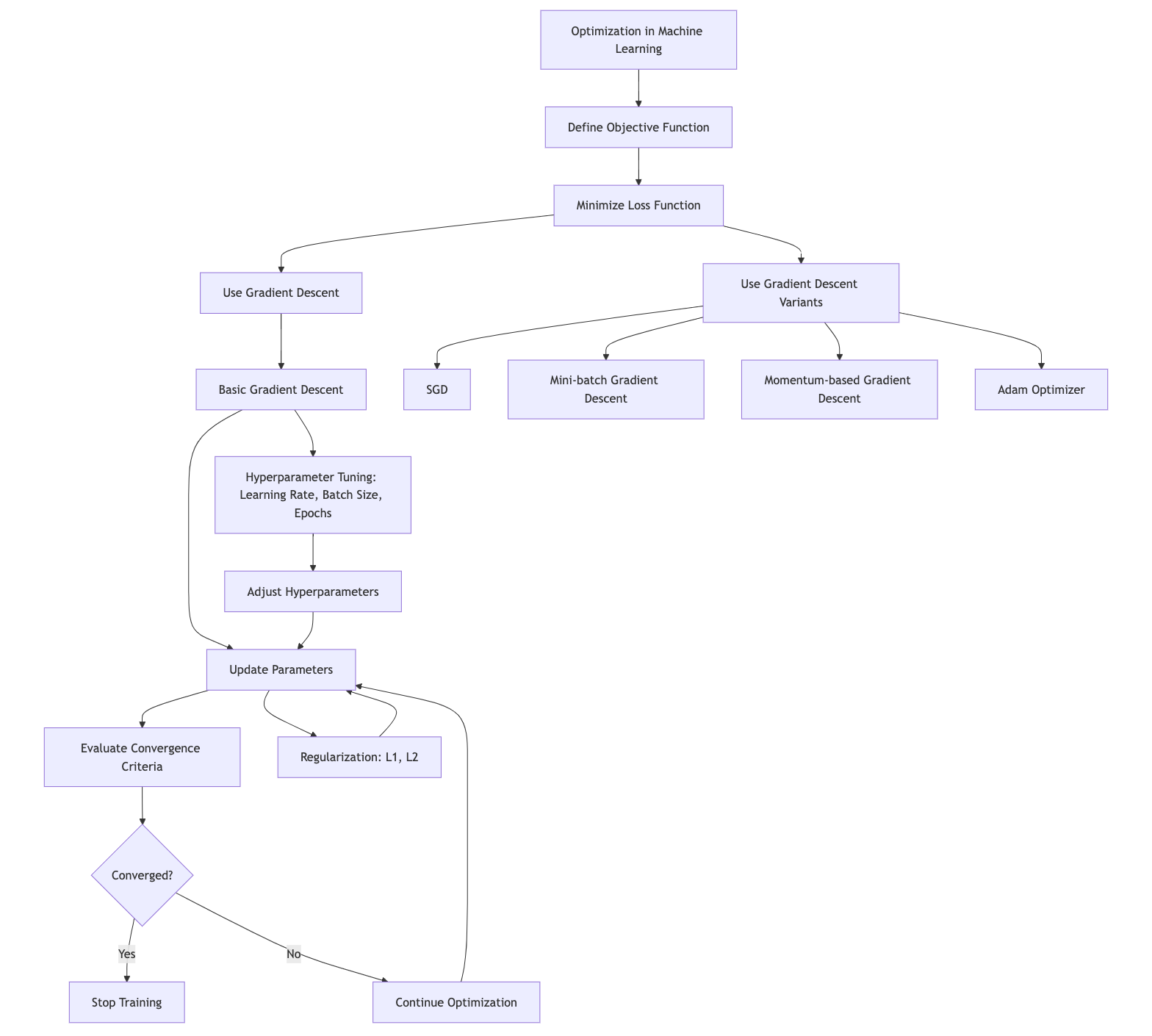
Figure 6: Optimization and hyperparameters tuning in Machine Learning.
In Rust, implementing gradient descent and a basic training loop can be done using fundamental Rust features and libraries like ndarray for handling arrays and matrices. Below is an example of implementing gradient descent in Rust for a simple linear regression model:
use ndarray::{Array1, Array2, Zip};
fn compute_loss(predictions: &Array1<f64>, targets: &Array1<f64>) -> f64 {
let n = predictions.len() as f64;
(predictions - targets).mapv(|x| x.powi(2)).sum() / (2.0 * n)
}
fn compute_gradient(x: &Array2<f64>, y: &Array1<f64>, theta: &Array1<f64>) -> Array1<f64> {
let m = y.len() as f64;
let predictions = x.dot(theta);
x.t().dot(&(predictions - y)) / m
}
fn adam_optimizer(
x: &Array2<f64>,
y: &Array1<f64>,
mut theta: Array1<f64>,
learning_rate: f64,
epochs: usize,
) -> Array1<f64> {
let mut m = Array1::zeros(theta.len()); // First moment vector
let mut v = Array1::zeros(theta.len()); // Second moment vector
let beta1 = 0.9;
let beta2 = 0.999;
let epsilon = 1e-8;
for t in 1..=epochs {
let gradient = compute_gradient(x, y, &theta);
// Update biased first moment estimate
m = beta1 * m + (1.0 - beta1) * gradient.clone();
// Update biased second moment estimate
v = beta2 * v + (1.0 - beta2) * gradient.mapv(|g| g.powi(2));
// Compute bias-corrected first moment estimate
let m_hat = m.clone() / (1.0 - beta1.powi(t as i32));
// Compute bias-corrected second moment estimate
let v_hat = v.clone() / (1.0 - beta2.powi(t as i32));
// Update parameters
theta = &theta - &(learning_rate * m_hat / (v_hat.mapv(|v| v.sqrt()) + epsilon)); // Explicit subtraction
}
theta
}
fn main() {
// Previous titanic dataset loaded and cleaned
// ...
let theta = Array1::zeros(train_features.ncols());
let learning_rate = 0.01;
let epochs = 1000;
let optimized_theta = adam_optimizer(&train_features, &train_labels, theta, learning_rate, epochs);
println!("Optimized parameters: {:?}", &optimized_theta);
let final_loss = compute_loss(&train_features.dot(&optimized_theta), &train_labels);
println!("Final loss: {:.4}", final_loss);
}
In this example, the compute_loss function calculates the mean squared error loss, which is the loss function used in linear regression. The compute_gradient function computes the gradient of the loss with respect to the model parameters (theta). The gradient_descent function then iteratively updates the parameters using the calculated gradients and the specified learning rate. The main function demonstrates how to set up the data, initialize the parameters, and run the gradient descent algorithm to optimize the parameters. The final loss value indicates how well the model fits the training data after optimization.
A typical training loop involves multiple iterations through the dataset, with periodic adjustments to hyperparameters such as the learning rate. Rust’s strong type system and memory safety guarantee efficient training loop implementations, even in computationally intensive tasks like neural network training. Learning rates can be adjusted dynamically using schedules such as step decay or exponential decay, where the learning rate decreases as the number of iterations increases, allowing the model to make finer adjustments as it converges.
Adjusting hyperparameters, such as the learning rate, is essential for ensuring that the optimization process converges to a good solution. In practice, hyperparameter tuning often involves running multiple training sessions with different hyperparameter values and selecting the combination that results in the best model performance. This can be done manually, through grid search, or by using more sophisticated techniques like random search or Bayesian optimization. Different combinations of hyperparameters tuning methods are tested to find the best-performing model.
Rust's strong type system and performance characteristics make it well-suited for implementing machine learning algorithms and optimization techniques. The explicit handling of data structures and memory management in Rust can lead to more efficient and reliable implementations, especially in the context of large-scale machine learning tasks.
In summary, optimization and training are fundamental processes in machine learning that determine how well a model fits the data. Gradient descent and its variants, combined with appropriate hyperparameter selection, play a crucial role in minimizing the loss function and achieving convergence. Regularization techniques ensure that the model generalizes well to unseen data, preventing overfitting. Rust’s performance and safety features make it a powerful tool for implementing these optimization algorithms and training machine learning models efficiently. By leveraging libraries such as ndarray, gradient descent and other training methods can be executed with the high performance required for large-scale machine learning tasks.
1.6. Rust Language Features for Machine Learning
Rust is a systems programming language that has gained significant traction in recent years due to its emphasis on safety, performance, and concurrency. These features make Rust particularly well-suited for machine learning applications, where efficient use of resources and reliable execution are paramount. In this section, we will explore the fundamental ideas behind Rust's features, delve into how its ownership model, lifetimes, and error handling contribute to building robust machine learning applications, and provide practical examples of leveraging Rust to optimize machine learning models and perform parallel computations.
At the core of Rust's appeal is its strict enforcement of memory safety without sacrificing performance. Unlike languages that rely on garbage collection, Rust uses a unique ownership model to manage memory. This model ensures that resources are automatically freed when they are no longer needed, preventing memory leaks and other common issues like dangling pointers or data races. In machine learning, where operations often involve large datasets and complex computations, Rust’s memory safety guarantees reduce the risk of runtime errors and undefined behavior, allowing developers to focus on algorithmic correctness rather than low-level memory management.
The ownership model in Rust revolves around the concepts of ownership, borrowing, and lifetimes. Ownership ensures that each value in Rust has a single owner, and when the owner goes out of scope, the value is automatically deallocated. Borrowing allows multiple references to a value, but only one of them can be mutable at a time, preventing data races. Lifetimes, on the other hand, ensure that references do not outlive the data they point to, which is crucial in avoiding use-after-free errors. In machine learning, where data manipulation and transformation are frequent, Rust’s ownership model ensures that operations on data are safe and free from concurrency issues.
Another key feature of Rust is its powerful type system and pattern matching, which contribute to robust error handling. Rust encourages the use of Result and Option types for handling errors and optional values, respectively, making it explicit when a function can fail or return nothing. This feature is particularly useful in machine learning, where operations like data parsing, model training, or file I/O can fail due to various reasons. By leveraging Rust’s type system, developers can handle errors gracefully and ensure that their machine learning applications are reliable and resilient.
Rust’s concurrency model is another significant advantage for machine learning. Rust provides built-in support for parallel and concurrent programming, making it easier to distribute computations across multiple cores or threads. This is crucial for machine learning tasks that involve heavy computation, such as training deep neural networks or processing large datasets. By using Rust’s concurrency features, developers can write parallel algorithms that take full advantage of modern multi-core processors, thereby speeding up the training and inference processes.
To illustrate how Rust’s features can be leveraged in machine learning, consider the following example where we implement a parallelized computation of a simple matrix multiplication. This operation is common in many machine learning algorithms, and optimizing it for performance can significantly impact the overall speed of model training and inference.
use rayon::prelude::*; // Rayon for parallel iterators
use ndarray::{Array2, Axis};
fn parallel_matrix_multiplication(a: &Array2<f64>, b: &Array2<f64>) -> Array2<f64> {
assert_eq!(a.shape()[1], b.shape()[0], "Matrix dimensions do not match for multiplication");
let rows = a.shape()[0];
let cols = b.shape()[1];
let mut result = Array2::zeros((rows, cols));
result.axis_iter_mut(Axis(0)).into_par_iter().enumerate().for_each(|(i, mut row)| {
for j in 0..cols {
row[j] = a.row(i).dot(&b.column(j));
}
});
result
}
fn main() {
let a = Array2::from_shape_vec((2, 3), vec![1.0, 2.0, 3.0, 4.0, 5.0, 6.0]).unwrap();
let b = Array2::from_shape_vec((3, 2), vec![7.0, 8.0, 9.0, 10.0, 11.0, 12.0]).unwrap();
let result = parallel_matrix_multiplication(&a, &b);
println!("Result of matrix multiplication:\n{:?}", result);
}
In this example, we use the ndarray crate for handling matrices and the rayon crate for parallel computation. The parallel_matrix_multiplication function multiplies two matrices in parallel by distributing the computation of each row of the result matrix across multiple threads. The use of Rust’s concurrency model ensures that the operation is both safe and efficient, taking full advantage of the available processing power.
Rust’s features also extend to interoperability with other languages and libraries, which is particularly beneficial in the machine learning domain. For instance, Rust can be integrated with Python using the pyo3 crate, allowing developers to leverage existing machine learning libraries like TensorFlow or PyTorch while implementing performance-critical components in Rust. This hybrid approach enables developers to benefit from Rust’s safety and performance without having to rewrite entire machine learning pipelines.
1.7. Conclusion
By the end of Chapter 1, readers will have a solid understanding of the machine learning problem, equipped with both the theoretical knowledge and practical skills needed to begin implementing machine learning solutions using Rust. This chapter sets the stage for more advanced topics, providing the necessary foundation to tackle complex machine learning challenges with confidence and precision.
1.7.1. Further Learning with GenAI
These prompts will guide you through technical discussions on machine learning principles and Rust implementations, ensuring a robust comprehension of the material.
Explain in detail how supervised, unsupervised, and reinforcement learning differ in terms of data requirements, learning objectives, and common algorithms. Provide examples of real-world applications for each type and discuss how Rust can be utilized to implement these types of learning models effectively.
Describe the complete machine learning pipeline, including data collection, preprocessing, model selection, training, evaluation, and deployment. For each stage, explain the specific considerations and challenges involved, and discuss how Rust’s features, such as memory safety and concurrency, can address these challenges.
Discuss the significance of data in machine learning and the impact of data quality on model performance. Provide an in-depth analysis of how Rust handles data differently than other programming languages and how these differences can be leveraged to improve data processing and model reliability.
Formulate a machine learning problem from a real-world scenario, detailing the steps to translate the problem into a machine learning context. Discuss how to identify and define input features (X) and target outputs (Y), and explore the challenges in this process. How can Rust’s type system and struct features be used to effectively represent and manage these components?
Compare and contrast different machine learning models, such as linear models, decision trees, SVMs, and neural networks, in terms of their strengths, weaknesses, and suitability for different types of problems. How does model selection affect the overall performance of a machine learning system, and what tools in Rust can assist in the selection process?
Explore the process of feature engineering in-depth, including techniques such as one-hot encoding, normalization, standardization, and polynomial features. Provide detailed examples of how each technique can be implemented in Rust, focusing on the libraries and tools available within the Rust ecosystem.
Discuss the importance of data normalization in machine learning, especially in models like SVMs and neural networks. Explain the mathematical principles behind normalization techniques such as Min-Max scaling and Z-score normalization, and provide a comprehensive guide on how to implement these techniques in Rust.
Analyze the bias-variance tradeoff in machine learning, explaining how it impacts model performance. Discuss strategies to balance bias and variance during model training, and provide examples of how Rust’s features, like type safety and efficient memory management, can help mitigate these issues.
Describe the cross-validation technique in detail, including its variants such as k-fold and leave-one-out cross-validation. Explain the importance of cross-validation in model evaluation and selection, and provide a step-by-step guide on how to implement cross-validation in Rust.
Explain the concept of gradient descent and its importance in training machine learning models. Compare different variants of gradient descent, such as batch, stochastic, and mini-batch gradient descent. Provide detailed instructions on how to implement gradient descent from scratch in Rust, including how to handle issues like learning rate decay and convergence.
Discuss the role of hyperparameters in machine learning models, focusing on how they influence model performance and the training process. Provide a detailed explanation of common hyperparameters in models like SVMs, decision trees, and neural networks, and guide the reader through the process of tuning these hyperparameters in Rust.
Provide a comprehensive overview of regularization techniques in machine learning, such as L1 (Lasso), L2 (Ridge), and Elastic Net. Explain the theoretical foundations of these techniques and how they help prevent overfitting. Offer detailed examples of how to implement these regularization methods in Rust.
Explore Rust’s ownership model and its impact on developing machine learning applications. Discuss how ownership, borrowing, and lifetimes in Rust contribute to safer, more reliable code, particularly in the context of handling large datasets and complex models.
Analyze the benefits of using Rust’s concurrency features in machine learning, particularly in training large-scale models. Discuss how concurrency can improve the efficiency of training processes, and provide examples of implementing parallel and concurrent computations in Rust.
Examine Rust’s error handling mechanisms, including Result and Option types. Discuss how these features can be used to create robust machine learning applications that gracefully handle errors and edge cases, ensuring higher reliability in production environments.
Discuss the principles of feature selection and dimensionality reduction in machine learning. Compare techniques like Principal Component Analysis (PCA) and Recursive Feature Elimination (RFE). Provide detailed instructions on how to implement these techniques in Rust, including the mathematical foundations and practical coding examples.
Explain the concept of probabilistic graphical models, including Bayesian Networks and Markov Random Fields. Discuss the applications of these models in machine learning, and provide detailed examples of how to implement them in Rust, focusing on inference and learning algorithms.
Provide an in-depth exploration of reinforcement learning, including key concepts like Markov Decision Processes, policy gradients, and Q-learning. Discuss the challenges in implementing reinforcement learning algorithms and provide step-by-step guidance on how to code these algorithms in Rust, leveraging its concurrency features.
Explore kernel methods in machine learning, particularly in the context of SVMs and Gaussian Processes. Discuss the mathematical foundations of kernel functions, their advantages in high-dimensional spaces, and provide comprehensive coding examples of implementing kernel-based algorithms in Rust.
Discuss the process of automating machine learning (AutoML), including model selection, hyperparameter optimization, and pipeline automation. Analyze the benefits and challenges of AutoML, and provide detailed guidance on how to implement AutoML systems in Rust, focusing on available libraries and tools.
Each prompt is designed to push your understanding of machine learning and Rust to new heights, encouraging you to think deeply, code meticulously, and innovate fearlessly. The knowledge and skills you gain here will not only set you apart but will also empower you to contribute meaningfully to the future of technology.
1.7.2. Hands On Practices
These exercises are designed to push your technical skills to the limit, offering a deep dive into the practical aspects of machine learning with Rust.
Task:
Choose a complex real-world scenario (e.g., predicting customer lifetime value or detecting fraudulent transactions). Formulate it as a machine learning problem, defining input features, target outputs, and suitable models.
Implementation:
Create a Rust struct to represent the problem, preprocess data, and implement a model training loop, discussing the challenges faced.
Task:
Implement multiple data normalization techniques (e.g., Min-Max scaling, Z-score) and apply them to a complex dataset.
Implementation:
Use Rust crates like ndarray and serde to normalize the data. Train a model on each normalized dataset and compare the effects on performance.
Task:
Develop a cross-validation pipeline supporting multiple models (e.g., linear regression, decision trees, SVMs) and techniques like stratified k-fold and nested cross-validation.
Implementation:
Use Rust's ndarray and linfa crates to create a modular cross-validation pipeline and evaluate model performance on a real-world dataset.
Task:
Implement gradient descent variants (e.g., batch, stochastic, mini-batch) to train a linear regression model and a neural network.
Implementation:
Write Rust code to support gradient descent algorithms, compare their convergence speed, accuracy, and discuss computational efficiency.
Task:
Design a scalable training process for a machine learning model using Rust's concurrency features, training it on a large-scale dataset.
Implementation:
Implement parallel data loading and model training using Rust’s async/await and multi-threading features. Analyze performance improvements.
Each of these exercises is designed to help you master both the theoretical and practical aspects of machine learning with Rust. Completing them will take your skills to the next level and prepare you for real-world machine learning challenges.
Comments