6.1. Introduction to Decision Tree link

Decision trees are a foundational machine learning technique used for both classification and regression tasks. They are intuitive models that mimic human decision-making processes by learning simple decision rules inferred from data features. Their structure consists of nodes, branches, and leaves, which together form a tree that represents the decisions leading to a particular outcome. The interpretability and flexibility of decision trees make them a valuable tool in exploratory data analysis and a building block for more complex ensemble methods like random forests and gradient boosting machines.

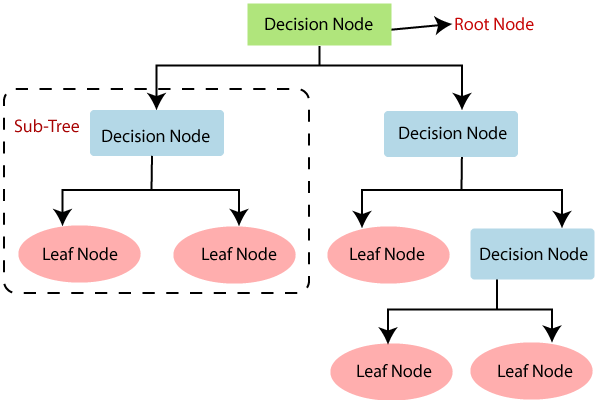
Figure 1: Illustration of decision tree model.

At the core of decision trees lies the concept of recursively partitioning the feature space to create regions with homogeneous target values. Consider a dataset $\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^N$, where $\mathbf{x}_i \in \mathbb{R}^d$ represents the feature vectors and $y_i$ denotes the target variable. A decision tree starts with a root node encompassing the entire dataset. It then splits this node into child nodes based on a decision rule applied to one of the features. Each node in the tree corresponds to a subset of the data, and each leaf node represents a final prediction.

The splitting process involves selecting a feature $x_j$ and a threshold $\theta$ such that the dataset $\mathcal{D}$ is divided into two subsets:

$$ \begin{align*} \mathcal{D}_{\text{left}} &= \{(\mathbf{x}_i, y_i) \mid x_{ij} \leq \theta\}, \\ \mathcal{D}_{\text{right}} &= \{(\mathbf{x}_i, y_i) \mid x_{ij} > \theta\}. \end{align*} $$

This process is repeated recursively on each child node, partitioning the feature space into regions where the target variable exhibits minimal variability. The nodes represent decision points, the branches represent the outcomes of these decisions, and the leaves represent the final output or prediction. The boundaries created by the splits are axis-aligned, forming hyperrectangles in the feature space. These decision boundaries enable the model to capture complex patterns by dividing the space into regions associated with specific target values.

The effectiveness of a decision tree largely depends on how the nodes are split, which involves selecting the optimal feature and threshold at each step. This selection is guided by impurity measures that quantify the homogeneity of the target variable within a node. Two widely used impurity measures are Gini impurity and entropy, which form the basis for criteria like the Gini index and information gain.

The Gini impurity for a node ttt is defined as:

$$G(t) = 1 - \sum_{k=1}^K p_k^2,$$

where $p_k$ is the proportion of samples belonging to class $k$ at node $t$, and $K$ is the total number of classes. A Gini impurity of zero indicates that all samples at the node belong to a single class, representing maximum purity.

The entropy at a node $t$ is given by:

$$ H(t) = -\sum_{k=1}^K p_k \log_2 p_k. $$

Entropy measures the amount of uncertainty or disorder in the node. A lower entropy signifies a more homogeneous node. The information gain is then calculated as the reduction in entropy due to the split:

$$ \Delta H = H(t) - \left( \frac{N_{\text{left}}}{N} H(t_{\text{left}}) + \frac{N_{\text{right}}}{N} H(t_{\text{right}}) \right), $$

where $N$ is the number of samples at node $t$, $t_{\text{left}}$ and $t_{\text{right}}$ are the child nodes resulting from the split, and $N_{\text{left}}$ and $N_{\text{right}}$ are their respective sample counts.

In regression tasks, the variance reduction is used as the splitting criterion. The variance at node $t$ is:

$$\text{Var}(t) = \frac{1}{N} \sum_{i=1}^N (y_i - \bar{y})^2,$$

where $\bar{y}$ is the mean of the target values at node $t$. The objective is to minimize the weighted average variance of the child nodes after the split.

Decision trees are capable of modeling non-linear relationships due to their hierarchical partitioning of the feature space. Each split can be viewed as introducing a non-linearity, allowing the model to adapt to complex data structures without requiring explicit feature transformations. However, this flexibility comes with the risk of overfitting, especially when the tree grows too deep.

The trade-off between tree depth and model complexity is a crucial consideration. A deeper tree can capture more intricate patterns but may also fit noise in the data, reducing its generalization ability. Conversely, a shallow tree may underfit, failing to capture essential relationships. To mitigate overfitting, techniques such as pre-pruning (stopping the tree growth early) and post-pruning (removing branches from a fully grown tree) are employed. Parameters like the minimum number of samples required to split a node or the maximum depth of the tree are adjusted to find an optimal balance.

Implementing a decision tree from scratch in Rust involves several steps, leveraging the language's performance and safety features. The linfa crate is a Rust machine learning library that provides tools for building and evaluating models, including decision trees.

To begin, the dataset is represented using suitable data structures, such as the ndarray crate, which offers n-dimensional array capabilities for Rust. Features and target variables are stored in arrays or matrices, facilitating efficient computations.

The decision tree is constructed by defining a TreeNode struct that contains information about the node's splitting feature, threshold, impurity measure, and references to its child nodes. The splitting process involves iterating over all possible features and thresholds to find the split that results in the maximum impurity reduction. This requires calculating the impurity measure for each potential split and selecting the one that optimizes the chosen criterion.

The recursive splitting function builds the tree by:

• Evaluating whether a node should be split based on stopping criteria, such as maximum depth or minimum number of samples.

• Selecting the best split by computing impurity measures for all possible feature-threshold combinations.

• Partitioning the data into left and right subsets based on the optimal split.

• Creating child TreeNode instances for the left and right branches.

• Recursively applying the splitting function to the child nodes.

For prediction, a traversal function is implemented. Given a new sample, the function starts at the root node and follows the decision rules (comparing feature values to thresholds) to navigate down the tree until it reaches a leaf node. The prediction is then the class label (for classification) or the mean target value (for regression) associated with that leaf.

Applying decision trees to classification tasks involves using datasets like the Iris dataset. After loading the data into Rust and splitting it into training and testing sets, the decision tree model is trained on the training data. The model's performance is evaluated on the test set using metrics such as accuracy, precision, recall, and the F1 score. The process highlights the model's ability to generalize to unseen data.

In regression tasks, such as predicting housing prices, the decision tree predicts continuous target values. The model is trained to minimize the variance within the leaf nodes. Performance metrics like Mean Squared Error (MSE), Mean Absolute Error (MAE), and R-squared are used to assess the model's predictive capabilities.

Decision trees offer a straightforward yet powerful approach to modeling complex datasets. Their ability to handle both categorical and numerical data, capture non-linear relationships, and provide interpretable models makes them a valuable asset in a data scientist's toolkit. By understanding the mathematical foundations of decision trees—such as impurity measures, recursive partitioning, and the balance between model complexity and generalization—practitioners can effectively leverage them for a variety of applications.

Rust's machine learning ecosystem, powered by the linfa crate, makes it easy to build and evaluate models like decision trees. Decision trees are intuitive models for classification tasks, and the Iris dataset is a great way to demonstrate this. In this example, we use linfa to load the Iris dataset, split it into training and test sets, and then train a decision tree classifier with Gini impurity as the criterion for split quality.

// Append Cargo.toml

[dependencies]
linfa = "0.7.0"
linfa-datasets = { version = "0.7.0", features = ["iris"] }
linfa-trees = "0.7.0"
ndarray = "0.15.0"

use std::{fs::File, io::Write};

use linfa::prelude::*;  
use linfa_trees::DecisionTree;
use ndarray::Array1;

fn main() {
    // Load the Iris dataset
    let (train, test) = linfa_datasets::iris().split_with_ratio(0.8);

    // Initialize the Decision Tree model
    let model = DecisionTree::params()
        .max_depth(Some(3)) 
        .split_quality(linfa_trees::SplitQuality::Gini);

    // Fit the model to the training data
    let decision_tree = model.fit(&train).unwrap();

    // Predict the labels of the test data
    let predictions: Array1<usize> = decision_tree.predict(test.records());

    // Evaluate the model
    let accuracy = predictions.confusion_matrix(&test).unwrap().accuracy();

    println!("Predicitions: {:?}", predictions);
    println!("Accuracy: {:.2}%", accuracy * 100.0);

    // Export trained tree graph to Tikz
    let tikz = decision_tree.export_to_tikz();
    let latex_tree: String = tikz.to_string();
    
    // Save trained tree graph in LaTex 
    let mut f = File::create("Decisio Tree Graph.tex").unwrap();
    f.write_all(latex_tree.as_bytes()).unwrap();
}

After training, the model is evaluated for accuracy on the test set, and the tree structure is exported as a LaTeX TikZ diagram. This allows you to visualize the decision-making process of the tree, offering deeper insights into the classification decisions.

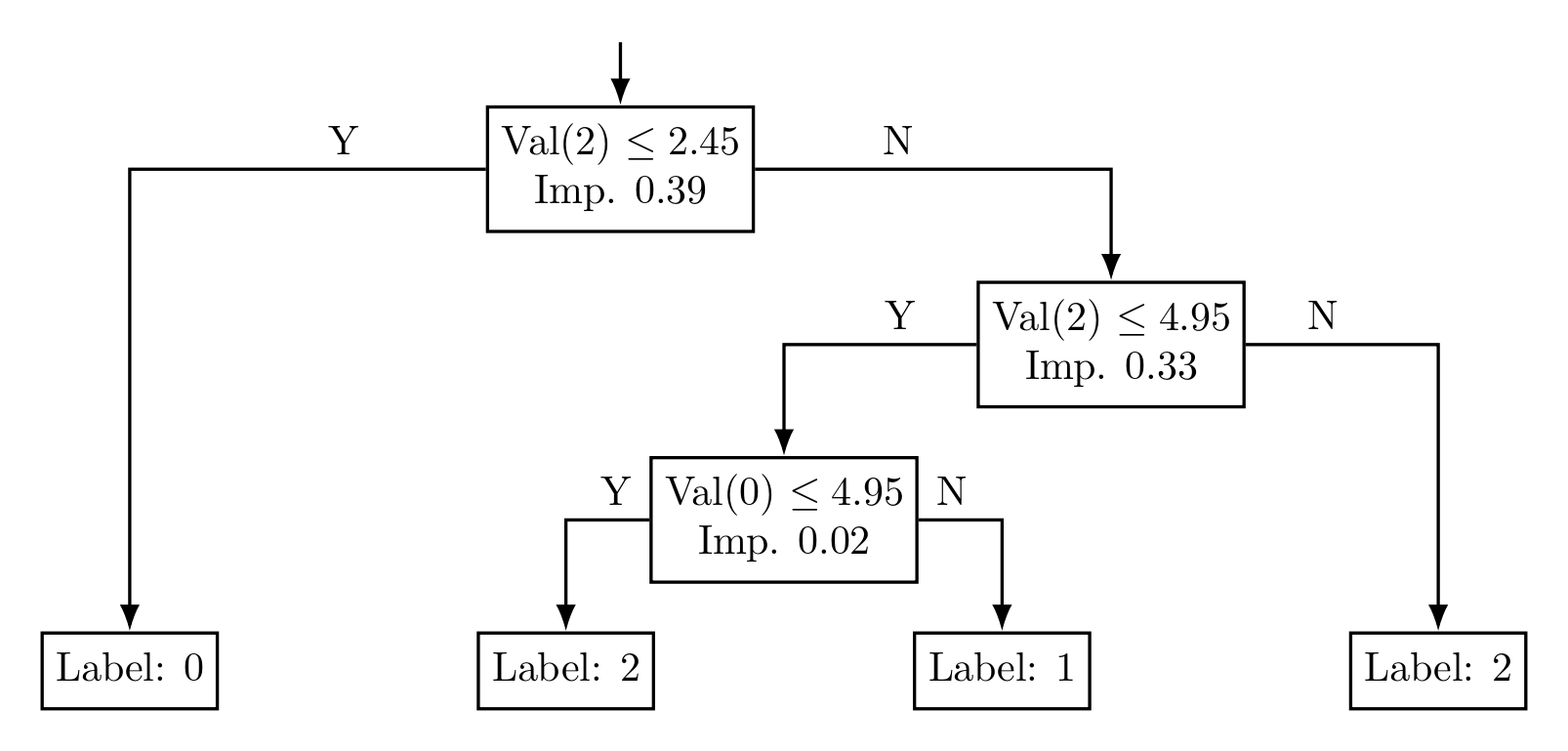
Figure 2: Visualized trained decision tree model

Implementing decision trees in Rust combines the language's performance advantages with the robustness required for machine learning tasks. Using crates like linfa facilitates the development process, allowing for efficient computations and integration with Rust's ecosystem. Whether applied to classification or regression problems, decision trees serve as a critical stepping stone towards mastering ensemble methods and advanced machine learning techniques.

6.2. Pruning and Regularization in Decision Trees link

Decision trees are a widely used machine learning model due to their interpretability and ability to handle both categorical and numerical data. However, a significant challenge with decision trees is their tendency to overfit the training data. Overfitting occurs when a model captures not only the underlying patterns but also the noise inherent in the training dataset, leading to poor generalization performance on unseen data. To mitigate overfitting, pruning and regularization techniques are essential, as they simplify the tree structure and enhance its predictive accuracy on new data.

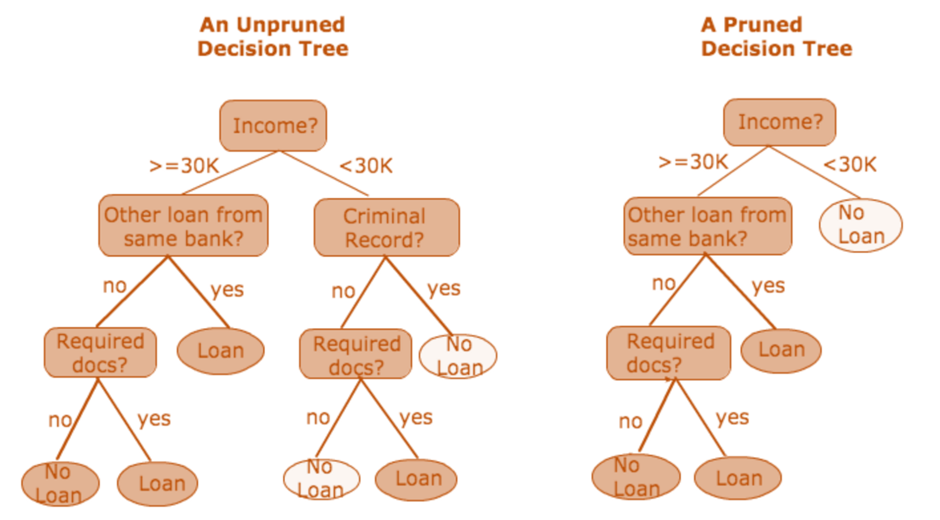
Figure 3: Pruning for decision tree.

The problem of overfitting in decision trees arises from their inherent flexibility. A fully grown decision tree can create complex models that perfectly classify the training data by partitioning the feature space into increasingly smaller regions. While this may minimize the training error, it often results in a model that is too tailored to the training data, failing to generalize to new, unseen instances. This phenomenon is well-documented in machine learning literature, including Bishop's Pattern Recognition and Machine Learning and Abu-Mostafa's Learning from Data, where the balance between model complexity and generalization is a central theme.

Pruning and regularization techniques address overfitting by restricting the complexity of the decision tree. Pruning involves removing branches that have little predictive power, effectively simplifying the tree. Regularization introduces constraints during the tree-building process, such as limiting the maximum depth or requiring a minimum number of samples to make a split. These techniques reduce the variance of the model, which is crucial for improving generalization performance.

Exploring different pruning techniques provides insight into how overfitting can be prevented. Two primary methods are pre-pruning (early stopping) and post-pruning (pruning after full tree growth). Pre-pruning halts the tree expansion before it perfectly fits the training data. This can be achieved by setting conditions such as a maximum depth, a minimum number of samples required to split a node, or a minimum impurity decrease. The decision to stop splitting is made during the tree construction, preventing the formation of branches that would only contribute to overfitting.

Post-pruning, on the other hand, involves growing the decision tree to its full depth and then trimming branches that do not contribute significantly to the model's predictive power. One common method is cost-complexity pruning, which introduces a complexity parameter α\\alphaα to balance the trade-off between the tree's complexity and its fit to the training data. The objective function for cost-complexity pruning is given by:

$$R_\alpha(T) = R(T) + \alpha \lvert T \rvert,$$

where $R(T)$ is the empirical risk (e.g., misclassification error for classification trees or mean squared error for regression trees), $\lvert T \rvert$ is the number of terminal nodes (leaves) in the tree $T$, and $\alpha$ is the complexity parameter. By adjusting $\alpha$, we can control the trade-off between the goodness of fit and the complexity of the tree, effectively pruning branches that do not sufficiently decrease the empirical risk to justify their added complexity.

Understanding the role of regularization parameters is crucial in controlling the complexity of decision trees. Parameters such as the minimum number of samples per leaf ($N_{\text{leaf}}^{\text{min}}$) and the maximum tree depth ($D_{\text{max}}$) directly influence the growth of the tree. Setting $N_{\text{leaf}}^{\text{min}}$ ensures that each leaf node represents a substantial portion of the data, preventing the model from capturing noise associated with very small subsets. Limiting $D_{\text{max}}$ restricts the number of levels in the tree, thereby controlling the granularity of the partitioning of the feature space.

The minimum impurity decrease ($\Delta I_{\text{min}}$) is another regularization parameter that determines whether a split at a node should occur based on the reduction in impurity. The impurity measures, such as Gini impurity for classification or variance reduction for regression, quantify the homogeneity of the target variable within a node. A split is only performed if it results in an impurity decrease greater than $\Delta I_{\text{min}}$, ensuring that only meaningful partitions that improve the model's predictive power are considered.

Implementing pruning techniques in Rust involves integrating these concepts into the decision tree algorithm. Rust's performance and safety features make it an excellent choice for building efficient machine learning models. Using the linfa crate, which provides a toolkit for classical Machine Learning implemented in Rust, we can develop decision trees that incorporate pruning and regularization.

To implement pre-pruning, we modify the recursive function that builds the decision tree to include checks for the regularization parameters. For instance, before splitting a node, we assess whether the maximum depth $D_{\text{max}}$ has been reached. If so, the node becomes a leaf, and the splitting process stops. We also check whether the number of samples at the node is less than $N_{\text{leaf}}^{\text{min}}$ or whether the impurity decrease $\Delta I$ is less than $\Delta I_{\text{min}}$. These conditions ensure that the tree does not grow beyond a complexity that is likely to result in overfitting.

For post-pruning, we first allow the decision tree to grow to its full depth. Afterward, we traverse the tree in a bottom-up manner to evaluate the impact of pruning each node. We calculate the cost-complexity pruning criterion $R_\alpha(T_t)$ for each subtree $T_t$ rooted at node $t$:

$$R_\alpha(T_t) = R(T_t) + \alpha \lvert T_t \rvert.$$

We compare $R_\alpha(T_t)$ with the cost of replacing the entire subtree with a single leaf node ttt, which has a cost $R(t) + \alpha$. If pruning the subtree results in a lower cost, we replace $T_t$ with node $t$. This process is repeated recursively, allowing us to find the optimal balance between the tree's complexity and its fit to the data based on the chosen $\alpha$.

Experimenting with different regularization parameters involves adjusting $N_{\text{leaf}}^{\text{min}}$, $D_{\text{max}}$, and $\alpha$ to observe their effects on the model's performance. We can use cross-validation to select the optimal values for these parameters. By partitioning the training data into folds, we train the model on a subset and validate it on the remaining data, iterating over a range of parameter values to find those that minimize the validation error.

Comparing the performance of pruned versus unpruned trees requires evaluating the models on both training and testing datasets. Metrics such as accuracy, precision, recall, and F1-score are appropriate for classification tasks, while mean squared error (MSE), mean absolute error (MAE), and R-squared ($R^2$) are suitable for regression tasks. Typically, an unpruned tree will exhibit lower training error but higher testing error due to overfitting. In contrast, a pruned tree should show a slightly higher training error but a lower testing error, indicating better generalization.

Applying these techniques to a real-world dataset, such as the UCI Machine Learning Repository's Wine Quality dataset, provides practical insights. The dataset consists of physicochemical properties of wines and their quality ratings, making it suitable for regression analysis. After loading the data into Rust and preprocessing it as necessary, we split it into training and testing sets. We then train both unpruned and pruned decision trees, adjusting the regularization parameters and recording the performance metrics.

Analyzing the results involves comparing the errors and variance of the models. Visualizing the relationship between the regularization parameters and the model's performance can be done by plotting the metrics against the parameter values. For example, plotting the testing error against $D_{\text{max}}$ may reveal that the error decreases initially but starts increasing after a certain depth due to overfitting. Similarly, observing the impact of $\alpha$ in post-pruning can help identify the optimal level of pruning.

Pruning and regularization are essential techniques in decision tree learning to prevent overfitting and improve model generalization. By understanding the fundamental and conceptual ideas behind these methods, we can effectively control the complexity of decision trees. Pruning simplifies the tree by removing branches that do not contribute significantly to predictive accuracy, while regularization parameters like minimum samples per leaf and maximum tree depth limit the model's capacity during training.

The decision tree classifier provided by the Linfa library offers parameters to control the depth of the tree, such as max_depth. By setting this parameter, we can prune the decision tree to prevent it from growing beyond a certain level. Now, let's move on to the code where we implement both an unpruned and a pruned decision tree model using the Iris dataset.

// Append Cargo.toml

[dependencies]
linfa = "0.7.0"
linfa-datasets = { version = "0.7.0", features = ["iris"] }
linfa-trees = "0.7.0"
ndarray = "0.16.1"

use linfa::prelude::*;
use linfa_datasets;
use linfa_trees::DecisionTree;
use std::error::Error;

fn main() -> Result<(), Box<dyn Error>> {
    // Load the Iris dataset
    let dataset = linfa_datasets::iris();

    // Split the dataset into training (80%) and testing (20%) sets
    let (train, test) = dataset.split_with_ratio(0.8);

    // Unpruned Decision Tree (no max depth)
    let unpruned_model = DecisionTree::params()
        .max_depth(None) // No limit on depth
        .fit(&train)?;

    // Predict using the unpruned model
    let y_pred_unpruned = unpruned_model.predict(&test);

    // Compute accuracy for the unpruned model
    let accuracy_unpruned = y_pred_unpruned
        .iter()
        .zip(test.targets().iter())
        .filter(|(pred, actual)| pred == actual)
        .count() as f64 / y_pred_unpruned.len() as f64;

    println!("Unpruned Model Accuracy: {:.2}%", accuracy_unpruned * 100.0);

    // Pruned Decision Tree (limit tree depth)
    let pruned_model = DecisionTree::params()
        .max_depth(Some(3)) // Limit depth to 3
        .fit(&train)?;

    // Predict using the pruned model
    let y_pred_pruned = pruned_model.predict(&test);

    // Compute accuracy for the pruned model
    let accuracy_pruned = y_pred_pruned
        .iter()
        .zip(test.targets().iter())
        .filter(|(pred, actual)| pred == actual)
        .count() as f64 / y_pred_pruned.len() as f64;

    println!("Pruned Model Accuracy (Depth 3): {:.2}%", accuracy_pruned * 100.0);

    Ok(())
}

In the code above, we load the Iris dataset and split it into training and testing sets. We then train two decision tree models: an unpruned model with no depth limitation and a pruned model restricted to a depth of 3. Both models make predictions on the test set, and we calculate their respective accuracies. The pruned model typically avoids overfitting by limiting its complexity, resulting in better generalization and similar or improved accuracy on the test data compared to the unpruned model.

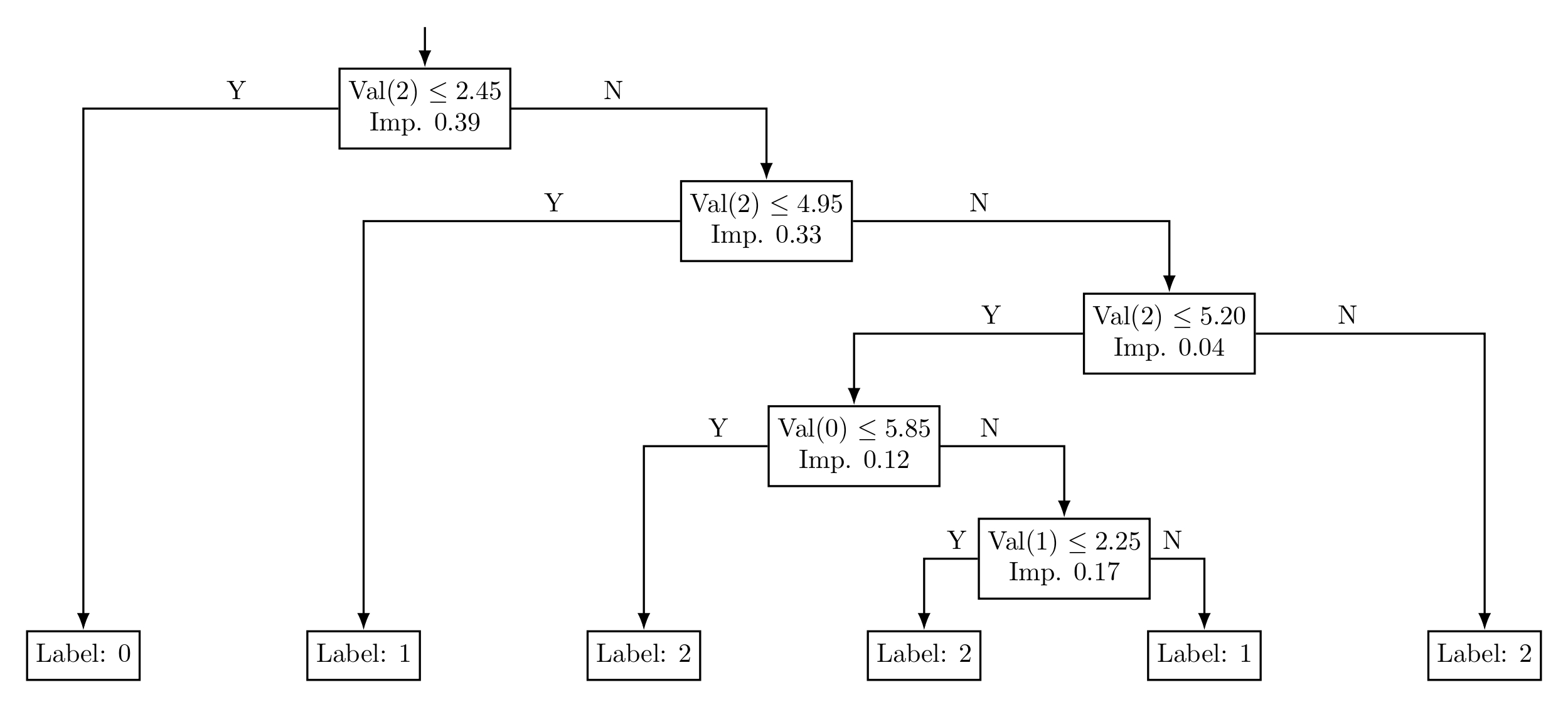
Figure 4: Decision Tree without Pruning

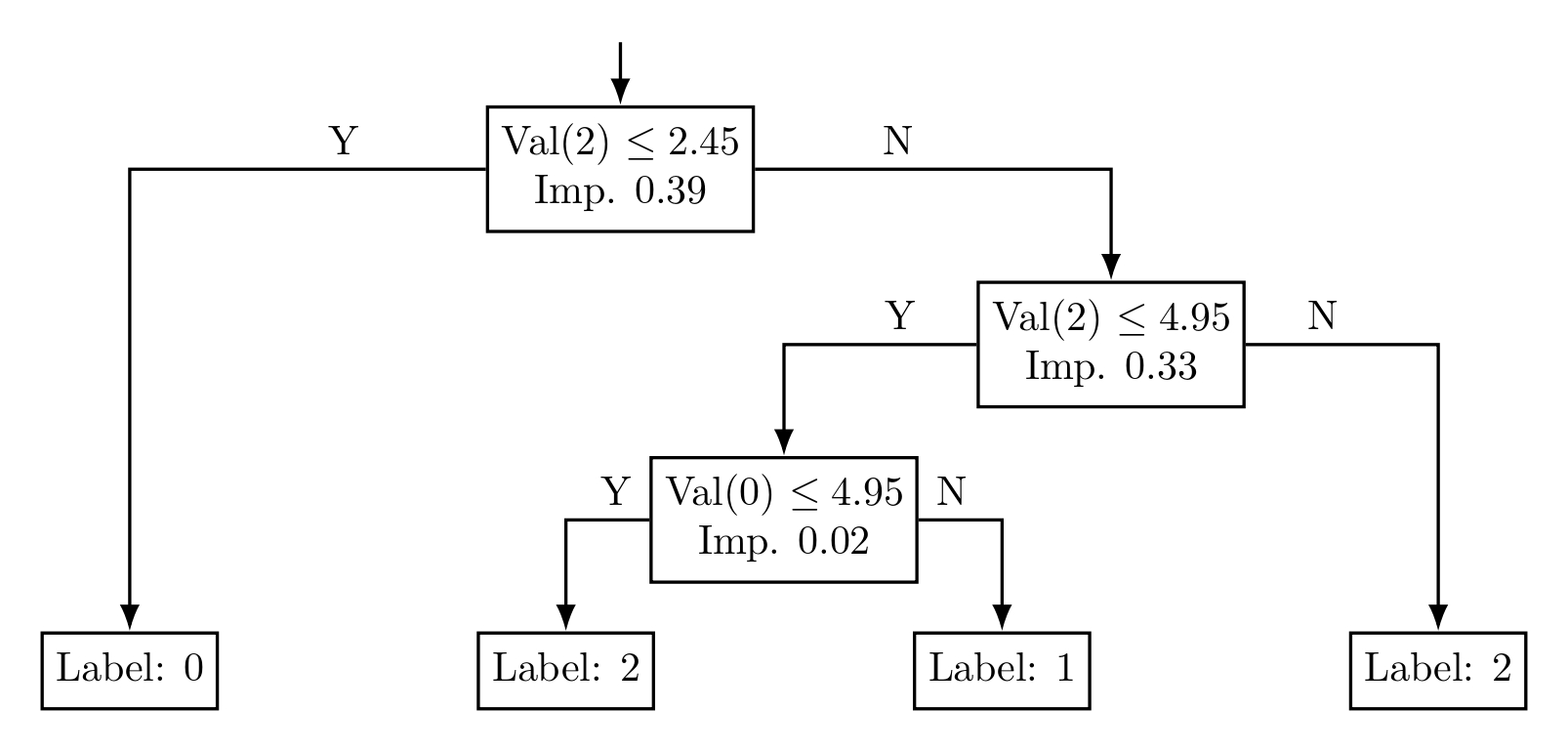
Figure 5: Pruned Decision Tree

Implementing these techniques in Rust, leveraging the linfa crate, allows for efficient and safe machine learning model development. Experimenting with different regularization parameters and pruning strategies on real-world datasets demonstrates the practical benefits of these methods. The balance between bias and variance, as discussed in Pattern Recognition and Machine Learning by Christopher Bishop and Learning from Data by Yaser Abu-Mostafa, is a critical aspect of model performance. Pruning and regularization help navigate this trade-off, leading to decision tree models that generalize well to new data.

6.3. Ensemble Methods: Bagging and Random Forests link

Ensemble methods have revolutionized machine learning by enhancing model performance through the combination of multiple base learners. The fundamental principle is that a collection of weak learners can form a strong learner when their outputs are appropriately combined. This concept is particularly potent when applied to decision trees, which, despite their simplicity and interpretability, are prone to overfitting and high variance. Two prominent ensemble techniques that leverage decision trees are Bagging (Bootstrap Aggregating) and Random Forests. These methods reduce variance and improve robustness by aggregating the predictions of multiple trees, each trained on different subsets of the data.

Bagging, introduced by Leo Breiman, stands for Bootstrap Aggregating and is designed to enhance the stability and accuracy of machine learning algorithms. The core idea involves generating multiple versions of a predictor and using these to get an aggregated predictor. Specifically, Bagging reduces variance by training each model on a different random subset of the training data, created through bootstrap sampling.

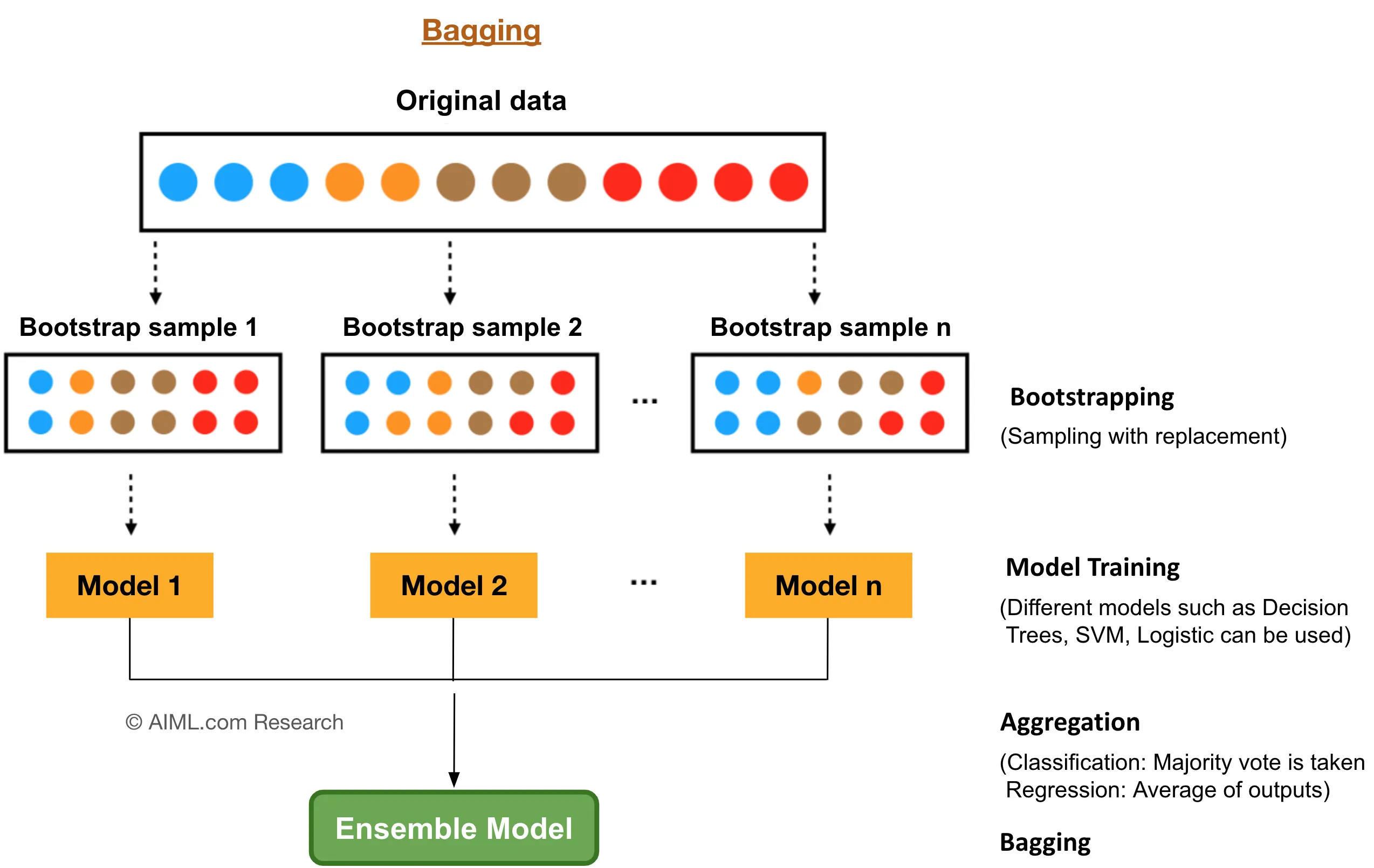
Figure 6: Bootstrap aggregation (bagging) model.

Formally, consider a dataset $\mathcal{D} = \{ (\mathbf{x}_i, y_i) \}_{i=1}^N$, where $\mathbf{x}_i \in \mathbb{R}^d$ represents the feature vectors and $y_i$ denotes the target variables. Bagging involves generating $B$ bootstrap samples $\mathcal{D}^{(b)}$ from $\mathcal{D}$, each of size $N$, by sampling with replacement. For each bootstrap sample $\mathcal{D}^{(b)}$, a decision tree $h^{(b)}$ is trained.

The aggregated prediction $\hat{y}$ for a new input $\mathbf{x}$ is obtained by averaging the predictions in regression tasks or by majority voting in classification tasks:

• Regression: $\hat{y} = \frac{1}{B} \sum_{b=1}^B h^{(b)}(\mathbf{x})$.

• Classification: $\hat{y} = \text{mode} \left\{ h^{(1)}(\mathbf{x}), h^{(2)}(\mathbf{x}), \ldots, h^{(B)}(\mathbf{x}) \right\}$.

Bagging effectively reduces the variance of the base estimator without increasing bias. Since decision trees are high-variance models, aggregating multiple trees trained on different datasets helps in smoothing out the fluctuations and leads to a more stable and robust model.

Random Forests extend the Bagging approach by introducing an additional layer of randomness. In addition to bootstrap sampling of the data, Random Forests inject randomness into the feature selection process during tree construction. At each split in the tree, a random subset of features is selected, and the best split is found only among these features. This technique reduces the correlation between individual trees, enhancing the ensemble's ability to generalize.

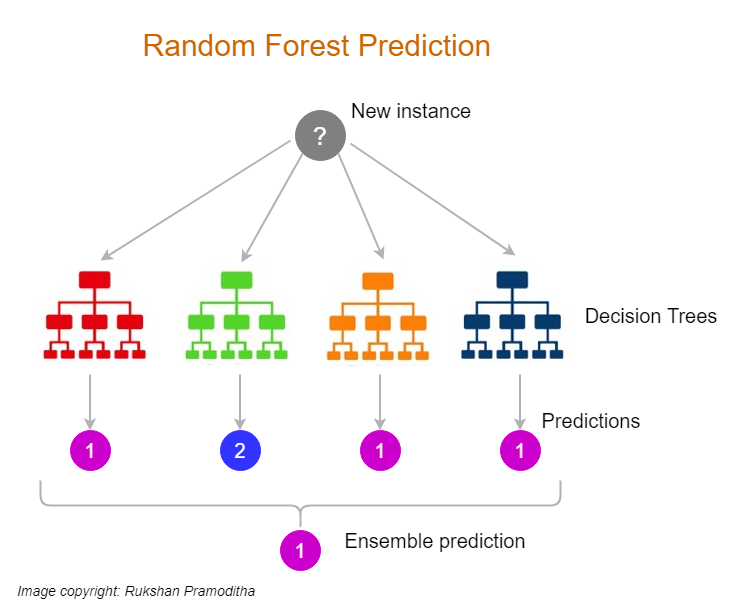
Figure 7: Random forest model.

The efficacy of Random Forests lies in two main concepts: bootstrap sampling and random feature selection, along with the use of out-of-bag (OOB) error estimation.

Bootstrap sampling creates diverse training sets by randomly sampling the original dataset with replacement. On average, each bootstrap sample includes about $63.2\%$ of the unique instances from $\mathcal{D}$, due to the properties of sampling with replacement. The remaining $36.8\%$ of the data not included in a particular bootstrap sample are called out-of-bag samples for that tree.

Out-of-bag error estimation provides an unbiased evaluation of the ensemble's performance without the need for a separate validation set. For each instance $(\mathbf{x}_i, y_i)$, predictions are made using only the trees for which $\mathbf{x}_i$ was an out-of-bag sample. The OOB error is computed by comparing these predictions to the true target values $y_i$. Mathematically, the OOB prediction for $\mathbf{x}_i$ is:

$$ \hat{y}_{\text{OOB}}^{(i)} = \frac{1}{|B_{\text{OOB}}^{(i)}|} \sum_{b \in B_{\text{OOB}}^{(i)}} h^{(b)}(\mathbf{x}_i), $$

where $B_{\text{OOB}}^{(i)}$ is the set of trees for which $\mathbf{x}_i$ is out-of-bag.

At each node during the construction of a decision tree in a Random Forest, a random subset of the features is selected. The number of features mmm considered at each split is a user-defined hyperparameter. Common choices are $m = \sqrt{d}$ for classification and $m = \frac{d}{3}$ for regression, where $d$ is the total number of features. The best split is then determined only among these mmm features.

This random selection of features at each split serves to decorrelate the trees in the ensemble. When trees are built using the same strong predictors, they tend to be correlated, and averaging correlated trees does not significantly reduce variance. By forcing each tree to consider different features, Random Forests promote diversity among the trees, leading to a greater reduction in variance when their predictions are aggregated.

Individual decision trees are prone to overfitting because they can capture noise in the training data due to their high variance nature. The variance of a decision tree can be significant, and small changes in the training data can lead to entirely different trees.

Random Forests mitigate this issue by averaging the predictions of multiple trees, thus reducing the overall variance of the model. The variance of the ensemble $\operatorname{Var}[\hat{y}]$ can be expressed as:

$$ \operatorname{Var}[\hat{y}] = \frac{\rho \sigma^2}{B} + (1 - \rho) \sigma^2, $$

where $\sigma^2$ is the variance of an individual tree, $\rho$ is the average correlation between trees, and $B$ is the number of trees. As $B$ increases, the first term $\frac{\rho \sigma^2}{B}$ diminishes, provided that $\rho$ is not too close to one. By reducing $\rho$ through random feature selection, Random Forests achieve a substantial reduction in variance compared to individual trees.

Furthermore, Random Forests maintain low bias, as each individual tree is an unbiased estimator if grown fully without pruning. The combination of low bias and reduced variance results in a model that generalizes well to new data.

Implementing a Random Forest algorithm in Rust involves utilizing the language's performance and safety features. The linfa crate is a Rust ecosystem for classical Machine Learning, which includes support for Random Forests through linfa-trees.

To implement a Random Forest in Rust, the following steps are undertaken:

• Data Preparation: Load the dataset using the linfa crate for preloaded datasets. Preprocess the data as necessary, handling missing values and encoding categorical variables.

• Bootstrap Sampling: For each tree, generate a bootstrap sample by randomly selecting NNN instances from the dataset with replacement. This can be achieved using Rust's random number generation capabilities.

• Random Feature Selection: Modify the tree-building algorithm to select a random subset of features at each split. At each node, randomly choose mmm features out of the total ddd features.

• Tree Construction: Build each decision tree using the bootstrap sample and the random feature selection at each node. The splitting criterion, such as Gini impurity for classification or variance reduction for regression, is applied only to the selected features.

• Aggregation of Predictions: For making predictions, aggregate the outputs of all trees. In regression, average the predictions; in classification, use majority voting.

• Out-of-Bag Error Estimation: Utilize the out-of-bag samples to estimate the generalization error. For each instance, aggregate predictions from trees where the instance was not included in the training sample and compare them to the true target values.

A Random Forest model is designed to enhance classification accuracy by utilizing multiple decision trees. We can implement one with the help of the Linfa library, which provides functionalities for bootstrap sampling and out-of-bag error estimation. Now, let's explore the code implementation.

// Append Cargo.toml

[dependencies]
linfa = "0.7.0"
linfa-datasets = { version = "0.7.0", features = ["iris"] }
linfa-trees = "0.7.0"
ndarray = "0.15.0"
rand = "0.8.5"

use std::collections::HashMap;

use linfa::prelude::*;
use linfa_datasets;
use linfa_trees::DecisionTree;
use ndarray::{Array1, Array2, ArrayBase, Axis, Dim, OwnedRepr};
use rand::thread_rng;

struct RandomForest {
    n_trees: usize,
    max_depth: Option<usize>,
}

impl RandomForest {
    fn fit(
        &self,
        dataset: &DatasetBase<
            ArrayBase<OwnedRepr<f64>, Dim<[usize; 2]>>,
            ArrayBase<OwnedRepr<usize>, Dim<[usize; 1]>>,
        >,
    ) -> Vec<DecisionTree<f64, usize>> {
        let mut trees = Vec::new();
        let sample_feature_size = (dataset.records().nrows(), dataset.records().ncols());

        let mut oob_predictions = vec![Vec::new(); dataset.records().nrows()];

        for tree_index in 0..self.n_trees {
            println!("Building tree {}/{}", tree_index + 1, self.n_trees);

            // Generate a bootstrap sample
            let bootstrap_sample = dataset
                .bootstrap(sample_feature_size, &mut thread_rng()).next().unwrap();

            // Get indices of the samples in the bootstrap sample
            let bootstrap_indices: HashMap<usize, usize> = bootstrap_sample
                .records().rows().into_iter().enumerate()
          		.map(|(index, row)| (row[0] as usize, index)).collect();

            // Train decision tree on bootstrap sample
            let tree = DecisionTree::params()
                .max_depth(self.max_depth)
                .fit(&bootstrap_sample)
                .unwrap();
            trees.push(tree);

            for (i, record) in dataset.records().outer_iter().enumerate() {
                if !bootstrap_indices.contains_key(&i) {
                    let pred = trees.last().unwrap().predict(&record.insert_axis(Axis(0)));
                    oob_predictions[i].push(pred[0]);
                }
            }
        }

        // Calculate the OOB error
        let oob_error = self.calculate_oob_error(&oob_predictions, dataset);

        println!("Out-of-Bag Error: {}", oob_error);
        trees
    }

    fn calculate_oob_error(
        &self,
        oob_predictions: &Vec<Vec<usize>>,
        dataset: &DatasetBase<
            ArrayBase<OwnedRepr<f64>, Dim<[usize; 2]>>,
            ArrayBase<OwnedRepr<usize>, Dim<[usize; 1]>>,
        >,
    ) -> f64 {
        let mut total = 0;
        let mut correct = 0;

        for (i, true_label) in dataset.targets().iter().enumerate() {
            if i < oob_predictions.len() && !oob_predictions[i].is_empty() {
                // Majority voting for OOB predictions
                let majority_vote = oob_predictions[i].iter()
                    .copied()
                    .fold(HashMap::new(), |mut acc, label| {
                        *acc.entry(label).or_insert(0) += 1;
                        acc
                    }).into_iter().max_by_key(|&(_, count)| count).map(|(label, _)| label).unwrap();

                if majority_vote == *true_label {
                    correct += 1;
                }
                total += 1;
            }
        }

        // Calculate accuracy if total is not zero
        if total > 0 {
            1.0 - (correct as f64 / total as f64) // OOB error = 1 - accuracy
        } else {
            1.0 // If no predictions, return error as 1 (100%)
        }
    }

    fn predict(&self, trees: &[DecisionTree<f64, usize>], features: Array2<f64>) -> Array1<usize> {
        let mut votes = Array2::<usize>::zeros((features.nrows(), trees.len()));
    
        // Each tree makes predictions for all samples
        for (i, tree) in trees.iter().enumerate() {
            let preds = tree.predict(&features);
            votes.column_mut(i).assign(&preds);
        }
    
        // Majority voting for each sample (row)
        let majority_votes: Array1<usize> = votes
            .axis_iter(Axis(0)) 
            .map(|row| {
                let mut counts = HashMap::new();
                for &label in row.iter() {
                    *counts.entry(label).or_insert(0) += 1;
                }
                counts.into_iter().max_by_key(|&(_, count)| count).map(|(label, _)| label).unwrap()
            })
            .collect();
    
        majority_votes
    }
    
}

fn main() {
    // Load Iris dataset
    let dataset = linfa_datasets::iris();
    let (train, test) = dataset.split_with_ratio(0.8);

    // Define Random Forest model
    let model = RandomForest {
        n_trees: 100,
        max_depth: Some(10),
    };

    // Train and predict using the model
    let trees = model.fit(&train);
    let predictions = model.predict(&trees, test.records().clone().to_owned());

    println!("Predictions: {:?}", predictions);
}

In the code, the Iris dataset is loaded, and a Random Forest model is trained. The model employs several decision trees, each trained on bootstrap samples of the dataset. Out-of-bag predictions are gathered for evaluating the model's performance. The final classification is determined by majority voting among the trees, leading to robust predictions and improved accuracy.

When applying Random Forests to complex datasets, it's crucial to evaluate their performance using robust methods such as cross-validation and to analyze feature importance.

Cross-validation involves partitioning the dataset into $k$ subsets (folds) and training the model $k$ times, each time using a different fold as the validation set and the remaining $k - 1$ folds as the training set. This approach provides an unbiased estimate of the model's performance.

Performance metrics for evaluation include:

• Classification: Accuracy, precision, recall, F1-score, and area under the ROC curve (AUC).

• Regression: Mean Squared Error (MSE), Mean Absolute Error (MAE), and coefficient of determination ($R^2$).

fn main() {
  	// ...
  
  	// Since we are doing classification
	// Use the test ground truth for comparison
    let ground_truth = test.targets().to_owned();

    // Create confusion matrix using predictions and ground truth
    let cm = predictions.confusion_matrix(&ground_truth).unwrap();

    // Print the confusion matrix
    println!("Confusion Matrix:\n{:?}", cm);
    
    // Compute accuracy, precision, recall, and F1-score
    let accuracy = cm.accuracy();
    let precision = cm.precision();
    let recall = cm.recall();
    let f1_score = cm.f1_score();

    println!("Accuracy: {}", accuracy);
    println!("Precision: {}", precision);
    println!("Recall: {}", recall);
    println!("F1-Score: {}", f1_score);
}

Adjusting hyperparameters is essential for optimizing the Random Forest's performance. Key hyperparameters include:

• Number of Trees (BBB): Increasing BBB generally improves performance but with diminishing returns and increased computational cost.

• Number of Features at Each Split (mmm): Balancing between reducing correlation (smaller mmm) and maintaining sufficient information for good splits (larger mmm).

• Maximum Depth of Trees: Limiting depth can prevent overfitting but may increase bias.

• Minimum Samples per Leaf: Ensuring that leaf nodes represent a sufficient portion of the data to avoid overfitting to noise.

Hyperparameter tuning can be performed using grid search or randomized search, evaluating the model's performance through cross-validation for each hyperparameter configuration.

Random Forests provide insights into feature importance, which can be valuable for understanding the model and the underlying data. Feature importance can be quantified in two main ways:

1. Mean Decrease in Impurity (MDI): For each feature, sum the total reduction in impurity (e.g., Gini impurity) it contributes across all trees. Formally, the importance of feature $f_j$ is $\text{Importance}(f_j) = \sum_{b=1}^B \sum_{t \in T_b} \Delta I(t) \cdot \mathbb{I}[f_t = f_j]$, where $\Delta I(t)$ is the impurity decrease at node $t$, $T_b$ is the set of nodes in tree $b$, $f_t$ is the feature used at node $t$, and $\mathbb{I}$ is the indicator function.

2. Permutation Importance: Measures the increase in model error when the values of a feature are randomly permuted. This method captures the dependency between features and can reveal the importance of features that interact with others.

Consider applying Random Forests to a complex dataset such as predicting customer churn in a telecommunications company. The dataset includes features like customer demographics, account information, and usage patterns.

• Data Loading and Preprocessing: Load the dataset using polars. Preprocess by handling missing values, encoding categorical variables (e.g., using one-hot encoding), and normalizing numerical features.

• Model Training: Initialize the Random Forest classifier with a specified number of trees and other hyperparameters. Train the model on the training data, using bootstrap sampling and random feature selection.

• Model Evaluation: Evaluate the model using cross-validation. Compute performance metrics such as accuracy, precision, recall, and F1-score to assess the model's ability to predict churn.

• Hyperparameter Tuning: Adjust hyperparameters to improve performance. For instance, increasing the number of trees or adjusting the number of features considered at each split.

• Feature Importance Analysis: Analyze which features are most important in predicting churn. This could reveal that usage patterns or contract length are significant predictors, providing actionable insights for the business.

// Append Cargo.toml

[dependencies]
csv = "1.3.0"
linfa = "0.7.0"
ndarray = "0.15.0"
polars = { version = "0.43.1", features = ["ndarray", "lazy", "dtype-full"] }
rand = "0.8.5"

use std::error::Error;

use linfa::prelude::*;
use ndarray::{Array1, Array2};
use polars::{lazy::dsl::col, prelude::*};
use rand::thread_rng;

fn one_hot_encode_df(df: DataFrame, column_names: &[&str]) -> DataFrame {
    let encoded = df
        .clone()
        .lazy() // Switch to lazy execution for transformations
        .select(
            df.get_column_names_owned()
                .into_iter()
                .map(|col_name| {
                    // If the column is in the list to be one-hot encoded, cast to Categorical first
                    if column_names.contains(&col_name.as_str()) {
                        col(col_name.clone())
                            .cast(DataType::Categorical(None, CategoricalOrdering::Physical))
                            .to_physical()
                    } else {
                        col(col_name.clone()) // Otherwise, use the column as is
                    }
                })
                .collect::<Vec<_>>(),
        )
        .collect()
        .unwrap(); // Collect into a DataFrame

    encoded
}

fn load_dataset() -> Result<DatasetBase<Array2<f64>, Array1<usize>>, Box<dyn Error>> {
    // Load the CSV file into a DataFrame
    let df = CsvReadOptions::default()
        .with_has_header(true)
        .try_into_reader_with_file_path(Some("telco_churn.csv".into()))?
        .finish()?;

    // Select only the relevant feature columns
    let selected_columns = [
        "gender",
        "SeniorCitizen",
        "Partner",
        "Dependents",
        "tenure",
        "PhoneService",
        "MultipleLines",
        "InternetService",
        "OnlineSecurity",
        "OnlineBackup",
        "DeviceProtection",
        "TechSupport",
        "StreamingTV",
        "StreamingMovies",
        "Contract",
        "PaperlessBilling",
        "PaymentMethod",
        "MonthlyCharges",
        "TotalCharges",
        "Churn",
    ];

    // Filter the DataFrame to include only the selected columns
    let df = df.select(selected_columns)?.drop_nulls::<String>(None)?;

    // Print the updated DataFrame
    println!("Dataframe: {}", df);

    let categorical_columns = [
        "gender",
        "Partner",
        "Dependents",
        "PhoneService",
        "MultipleLines",
        "InternetService",
        "OnlineSecurity",
        "OnlineBackup",
        "DeviceProtection",
        "TechSupport",
        "StreamingTV",
        "StreamingMovies",
        "Contract",
        "PaperlessBilling",
        "PaymentMethod",
        "Churn",
    ];
    let encoded_df = one_hot_encode_df(df, &categorical_columns);

    println!("One hot encoded dataframe: {}", encoded_df);

    let mut features_df = encoded_df.drop("Churn")?;
    let target_series = encoded_df.select(["Churn"])?;

    let mut file = std::fs::File::create("res.csv").unwrap();
    CsvWriter::new(&mut file).finish(&mut features_df).unwrap();

    // Convert features DataFrame to an ndarray
    let features: Array2<f64> = features_df.to_ndarray::<Float64Type>(IndexOrder::C)?;

    // Convert target Series to an ndarray
    let targets: Array1<usize> = target_series
        .to_ndarray::<Int32Type>(IndexOrder::C)?
        .into_shape((target_series.shape().0,))?
        .mapv(|x| x as usize);

    println!("Features: {:?}", features);
    println!("Targets: {:?}", targets);

    // Create the Dataset object
    let dataset = Dataset::new(features, targets);

    Ok(dataset)
}

fn main() {
    let dataset = load_dataset().unwrap();
    let (train, test) = dataset.shuffle(&mut thread_rng()).split_with_ratio(0.8);

    // Define Random Forest model
    let model = RandomForest {
        n_trees: 100,
        max_depth: Some(10),
    };

    // Train and predict using the model
    let trees = model.fit(&train);
    let predictions = model.predict(&trees, test.records().clone().to_owned());

    println!("Predictions: {:?}", predictions);
}

In this example, the code begins by loading a CSV dataset using polars, where it filters specific columns and removes rows with missing values. Categorical columns are one-hot encoded. The features and target columns are then converted into ndarray structures. A Random Forest model with 100 trees and a max depth of 10 is trained on 80% of the dataset, followed by making predictions on the test set.

Bagging and Random Forests are powerful ensemble methods that significantly enhance the performance of decision tree models by reducing variance and improving generalization. Bagging achieves this by training multiple trees on different subsets of the data and aggregating their predictions. Random Forests take this a step further by incorporating random feature selection, which decorrelates the trees and leads to a more robust ensemble.

Implementing Random Forests in Rust, leveraging the linfa crate, combines the efficiency and safety of Rust with the power of ensemble learning. By applying Random Forests to complex datasets, thoroughly evaluating their performance, and analyzing feature importance, practitioners can build models that not only perform well but also provide valuable insights into the data.

6.4. Boosting (AdaBoost, Gradient Boosting) link

Boosting is a powerful ensemble technique in machine learning that focuses on reducing bias by sequentially training a series of weak learners to form a strong learner. The fundamental idea behind boosting is to combine several weak classifiers, which individually may perform slightly better than random guessing, into a composite model that achieves high accuracy. At its core, boosting operates by training weak learners sequentially, where each subsequent learner focuses more on the instances that were misclassified by its predecessors. This is achieved by assigning weights to the training data and adjusting these weights after each iteration to emphasize the misclassified instances. The two most prominent boosting algorithms are AdaBoost (Adaptive Boosting) and Gradient Boosting, each employing different strategies to optimize the learning process.

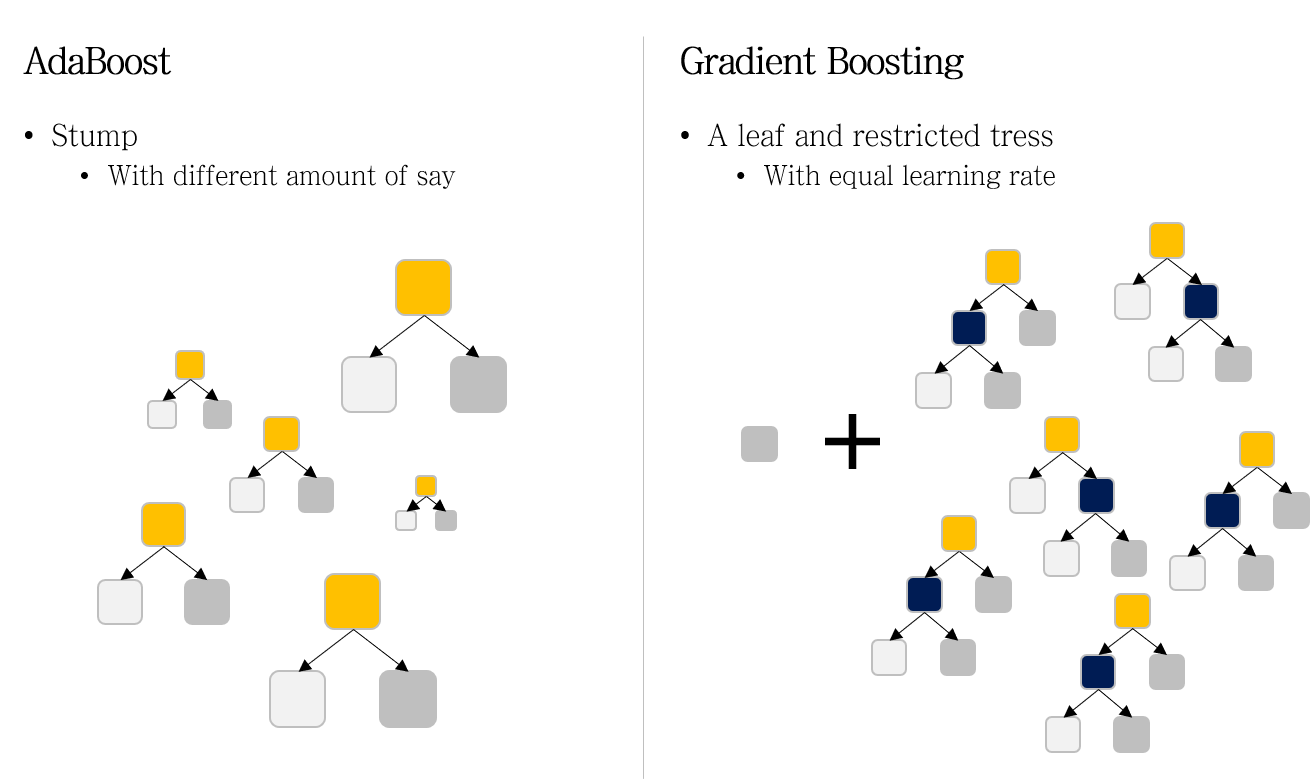
Figure 8: AdaBoost and Gradient Boosting models.

AdaBoost, introduced by Freund and Schapire, is one of the earliest and most influential boosting algorithms. It works by iteratively training weak learners on weighted versions of the training data. The key steps of AdaBoost can be formalized as follows:

Given a training dataset $\{(x_i, y_i)\}_{i=1}^N$, where $x_i \in \mathbb{R}^d$ and $y_i \in \{-1, +1\}$, the algorithm initializes a weight distribution $D_1(i) = \frac{1}{N}$ for all $i$.

For each iteration $t = 1, 2, \dots, T$:

• Train a weak learner $h_t(x)$ using the weight distribution $D_t$.

• Compute the weighted error: $\epsilon_t = \sum_{i=1}^N D_t(i) \cdot \mathbb{I}[y_i \neq h_t(x_i)],$, where $\mathbb{I}[\cdot]$ is the indicator function.

• Calculate the learner's weight: $\alpha_t = \frac{1}{2} \ln\left(\frac{1 - \epsilon_t}{\epsilon_t}\right)$.

• Update the weights for the next iteration: $D_{t+1}(i) = \frac{D_t(i) \exp(-\alpha_t y_i h_t(x_i))}{Z_t},$, where $Z_t$ is a normalization factor ensuring that$\sum_{i=1}^N D_{t+1}(i) = 1$ .

The final strong classifier is a weighted majority vote of the weak learners:

$$ H(x) = \operatorname{sign}\left(\sum_{t=1}^T \alpha_t h_t(x)\right). $$

AdaBoost focuses on instances that are difficult to classify by increasing their weights, thereby forcing subsequent learners to concentrate on these hard cases. This iterative reweighting effectively reduces the bias of the composite model.

Gradient Boosting, introduced by Friedman, generalizes the boosting approach by optimizing a loss function using gradient descent techniques in function space. Unlike AdaBoost, which focuses on classification errors, Gradient Boosting minimizes a differentiable loss function, making it suitable for both regression and classification tasks.

The Gradient Boosting algorithm starts by initializing the model with a constant value that minimizes the loss function across all training instances. This initial model is defined as $F_0(x) = \arg\min_{\gamma} \sum_{i=1}^N L(y_i, \gamma)$, where $L$ is the chosen loss function, $y_i$ are the true labels, and $\gamma$ is a constant value to be determined.

For each iteration $t = 1, 2, \dots, T$, the algorithm performs several key steps to refine the model. It begins by computing the negative gradients, also known as pseudo-residuals, for each training instance. These pseudo-residuals are calculated using the partial derivative of the loss function with respect to the current model's predictions:

$$ r_{it} = -\left[\frac{\partial L(y_i, F_{t-1}(x_i))}{\partial F_{t-1}(x_i)}\right]. $$

This step effectively measures the direction and magnitude by which the current model's predictions need to be adjusted to minimize the loss.

Next, the algorithm fits a weak learner $h_t(x)$ to these pseudo-residuals $r_{it}$. The weak learner is trained to predict the negative gradients, aiming to capture the errors made by the current model $F_{t-1}(x)$. By focusing on these residuals, the weak learner directly addresses the shortcomings of the previous model iteration.

After fitting the weak learner, the algorithm computes the optimal step size $\gamma_t$ that will scale the weak learner's contribution to the model. This is achieved by solving the following optimization problem:

$$ \gamma_t = \arg\min_{\gamma} \sum_{i=1}^N L\left(y_i, F_{t-1}(x_i) + \gamma h_t(x_i)\right). $$

This step determines how much weight the new weak learner should have in the updated model to minimize the overall loss.

Finally, the model is updated by adding the scaled weak learner to the previous model:

$$ F_t(x) = F_{t-1}(x) + \gamma_t h_t(x). $$

This additive update incorporates the improvements suggested by the weak learner, refining the model's predictions. The process repeats for $T$ iterations, progressively enhancing the model's accuracy.

The final model $F_T(x)$ is thus an ensemble of the initial model and all the scaled weak learners accumulated over the iterations:

$$ F_T(x) = F_0(x) + \sum_{t=1}^T \gamma_t h_t(x). $$

Gradient Boosting works by fitting each new learner to the negative gradient of the loss function, effectively performing gradient descent in function space. This approach allows the algorithm to optimize a wide range of loss functions, providing flexibility in addressing different types of problems. By iteratively focusing on the residual errors and updating the model accordingly, Gradient Boosting constructs a strong predictive model from multiple weak learners.

Boosting algorithms iteratively improve the model by focusing on instances that are harder to predict. In AdaBoost, this is achieved by increasing the weights of misclassified instances, whereas in Gradient Boosting, the model learns from the residual errors directly. Both methods combine weak learners into a strong learner by weighting their contributions, leading to improved performance.

The learning rate (also known as the shrinkage parameter) is a crucial hyperparameter in boosting algorithms, particularly in Gradient Boosting. It controls the contribution of each weak learner to the final model. A smaller learning rate requires more iterations but can lead to better generalization by preventing overfitting. Overfitting in boosting can occur if the weak learners are too complex or if the model is trained for too many iterations. Regularization techniques, such as limiting the depth of decision trees or introducing subsampling, can mitigate overfitting.

The choice of loss function $L(y, F(x))$ plays a significant role in Gradient Boosting. Common loss functions include:

• Squared Error Loss for regression tasks: $L(y, F(x)) = \frac{1}{2}(y - F(x))^2.$

• Exponential Loss (used in AdaBoost): $L(y, F(x)) = \exp(-y F(x)).$

• Deviance (Logistic Loss) for classification: $L(y, F(x)) = \ln\left(1 + \exp(-2 y F(x))\right).$

Selecting an appropriate loss function aligns the boosting algorithm with the specific problem, influencing both the convergence behavior and the robustness of the model.

Implementing AdaBoost and Gradient Boosting in Rust can be achieved by creating custom implementations that offer greater control and insight into the mechanics of these boosting algorithms. AdaBoost works by iteratively training weak classifiers, adjusting the weights of misclassified data points, and combining them into a strong classifier. Gradient Boosting, on the other hand, sequentially adds decision trees that correct errors from previous trees, optimizing a loss function step by step. This hands-on approach provides a deep understanding of the ensemble learning process.

This Rust implementation demonstrates how AdaBoost can be constructed using a decision stump as the weak learner, training on weighted samples, and adjusting for errors at each step.

// Append Cargo.toml

[dependencies]
ndarray = "0.16.1"
rand = "0.8.5"

use ndarray::{Array1, Array2};
use rand::Rng;
use std::f64;

// Example AdaBoost implementation
struct AdaBoost {
    n_rounds: usize,
}

impl AdaBoost {
    fn new(n_rounds: usize) -> Self {
        AdaBoost { n_rounds }
    }

    fn fit(&self, x: &Array2<f64>, y: &Array1<i32>) -> Vec<(f64, Array1<i32>)> {
        let n_samples = x.nrows();
        let mut weights = Array1::from_elem(n_samples, 1.0 / n_samples as f64);
        let mut classifiers = Vec::new();

        for _ in 0..self.n_rounds {
            let weak_learner = self.train_weak_learner(x, y, &weights);
            let predictions = self.predict_weak_learner(&weak_learner, x);
            
            let mut weighted_error = 0.0;
            for i in 0..n_samples {
                if predictions[i] != y[i] {
                    weighted_error += weights[i];
                }
            }
            
            if weighted_error > 0.5 {
                continue;
            }

            let alpha = 0.5 * ((1.0 - weighted_error) / weighted_error).ln();
            classifiers.push((alpha, predictions.clone()));

            for i in 0..n_samples {
                if predictions[i] == y[i] {
                    weights[i] *= (weighted_error / (1.0 - weighted_error)).sqrt();
                } else {
                    weights[i] *= ((1.0 - weighted_error) / weighted_error).sqrt();
                }
            }

            let sum_weights: f64 = weights.sum();
            weights /= sum_weights; // Normalize weights
        }

        classifiers
    }

    fn train_weak_learner(&self, x: &Array2<f64>, y: &Array1<i32>, weights: &Array1<f64>) -> Array1<i32> {
        // Example: Simple decision stump based on random feature
        let n_features = x.ncols();
        let mut rng = rand::thread_rng();
        let chosen_feature = rng.gen_range(0..n_features);

        // Naive approach: split on the median of the chosen feature
        let median = x.column(chosen_feature).mean().unwrap_or(0.0);
        x.column(chosen_feature)
            .mapv(|x| if x >= median { 1 } else { -1 })
    }

    fn predict_weak_learner(&self, weak_learner: &Array1<i32>, x: &Array2<f64>) -> Array1<i32> {
        weak_learner.clone() // Simple decision stump prediction
    }

    fn predict(&self, classifiers: &[(f64, Array1<i32>)], x: &Array2<f64>) -> Array1<i32> {
        let mut final_prediction = Array1::zeros(x.nrows());

        for (alpha, predictions) in classifiers.iter() {
            for i in 0..x.nrows() {
                final_prediction[i] += alpha * predictions[i] as f64;
            }
        }

        final_prediction.mapv(|x: f64| if x >= 0.0 { 1 } else { -1 })
    }
}

fn main() {
    // Example usage with dummy data
    let x = Array2::from_shape_vec((4, 2), vec![5.0, 2.0, 2.0, 1.0, 2.0, 1.0, 5.0, 2.0]).unwrap();
    let y = Array1::from_vec(vec![1, -1, 1, -1]);

    let ada_boost = AdaBoost::new(10);
    let classifiers = ada_boost.fit(&x, &y);
    
    let predictions = ada_boost.predict(&classifiers, &x);
    println!("Predictions: {:?}", predictions);
}

The WeakLearner can be a simple decision stump or any classifier slightly better than random guessing. After training, predictions are made by taking the weighted majority vote of the weak learners.

For Gradient Boosting, the implementation involves defining a gradient boosting regressor or classifier that maintains the ensemble of weak learners. The training loop computes the pseudo-residuals, fits new learners, and updates the model accordingly.

Here’s an implementation of a Gradient Boosting model using Rust and the linfa crate:

// Append Cargo.toml

[dependencies]
linfa = "0.7.0"
linfa-datasets = { version = "0.7.0", features = ["iris"] }
linfa-trees = "0.7.0"
ndarray = "0.15.0"
rand = "0.8.5"

use ndarray::{Array1, Array2};
use linfa::prelude::*;
use linfa_trees::DecisionTree;
use rand::thread_rng;
use std::error::Error;

// Example Gradient Boosting implementation
struct GradientBoosting {
    n_rounds: usize,
    learning_rate: f64,
    max_depth: usize,
}

impl GradientBoosting {
    fn new(n_rounds: usize, learning_rate: f64, max_depth: usize) -> Self {
        GradientBoosting {
            n_rounds,
            learning_rate,
            max_depth,
        }
    }

    fn fit(&self, x: &Array2<f64>, y: &Array1<usize>) -> Vec<DecisionTree<f64, usize>> {
        let n_samples = x.nrows();
        let mut predictions: Array1<f64> = Array1::zeros(n_samples);
        let mut trees = Vec::new();

        for _ in 0..self.n_rounds {
            let residuals = y.mapv(|label| label as f64) - &predictions;

            let tree = self.train_weak_learner(x, &residuals);
            let tree_predictions = self.predict_weak_learner(&tree, x);

            predictions += &(self.learning_rate * tree_predictions);
            trees.push(tree);
        }

        trees
    }

    fn train_weak_learner(&self, x: &Array2<f64>, residuals: &Array1<f64>) -> DecisionTree<f64, usize> {
        let dataset = linfa::Dataset::new(x.clone(), residuals.mapv(|r| r.round() as usize)); // Convert residuals to usize

        // Initialize and fit the Decision Tree model
        let model = DecisionTree::params()
            .max_depth(Some(self.max_depth))
            .fit(&dataset)
            .unwrap();

        model
    }

    fn predict_weak_learner(&self, weak_learner: &DecisionTree<f64, usize>, x: &Array2<f64>) -> Array1<f64> {
        weak_learner.predict(x).mapv(|label| label as f64) // Convert predictions to f64
    }

    fn predict(&self, trees: &Vec<DecisionTree<f64, usize>>, x: &Array2<f64>) -> Array1<usize> {
        let mut final_prediction = Array1::zeros(x.nrows());

        for tree in trees.iter() {
            let tree_predictions = tree.predict(x).mapv(|label| label as f64); // Convert predictions to f64
            final_prediction += &tree_predictions;
        }

        // Convert accumulated predictions to class labels
        final_prediction.mapv(|pred| {
            if pred < 0.5 { 0 }
            else if pred < 1.5 { 1 }
            else { 2 }
        })
    }
}

fn main() -> Result<(), Box<dyn Error>> {
    // Load the Iris dataset
    let (train, test) = linfa_datasets::iris().shuffle(&mut thread_rng()).split_with_ratio(0.8);

    // Train the Gradient Boosting model
    let gradient_boosting = GradientBoosting::new(100, 0.1, 3); // 100 rounds, learning rate of 0.1, max depth of 3
    let trees = gradient_boosting.fit(&train.records(), &train.targets());

    // Make predictions
    let predictions = gradient_boosting.predict(&trees, &test.records());

    // Calculate accuracy
    let true_labels = test.targets();
    let correct_predictions = predictions.iter()
        .zip(true_labels.iter())
        .filter(|(pred, true_label)| *pred == *true_label)
        .count();
  
    let accuracy = correct_predictions as f64 / predictions.len() as f64 * 100.0;

    println!("Predictions: {:?}", predictions);

    println!("Accuracy: {:.2}%", accuracy);

    Ok(())
}

In this implementation, we define a GradientBoosting struct that encapsulates the number of boosting rounds, learning rate, and the maximum depth of the decision trees. The fit method trains the model by iteratively updating the predictions based on the residuals from previous rounds. The resulting model is able to predict the class labels effectively, showcasing the versatility of Rust for implementing machine learning algorithms.

Hyperparameters such as the learning rate, number of iterations, and maximum depth of the trees can be tuned to optimize performance. The use of parallel computation and efficient data structures in Rust enhances the scalability of the implementation.

Applying AdaBoost and Gradient Boosting to datasets requires careful preprocessing, including handling missing values and encoding categorical variables. The models can be evaluated using cross-validation techniques to assess their generalization capabilities.

Tuning hyperparameters is essential for achieving optimal performance. Grid search or random search methods can be employed to explore the hyperparameter space. Metrics such as accuracy, precision, recall, and F1-score (for classification) or mean squared error and R-squared (for regression) are used to compare the performance of boosting algorithms with other ensemble methods like bagging and random forests.

In practice, Gradient Boosting often outperforms other methods due to its flexibility and ability to optimize custom loss functions. However, it may require more careful tuning to prevent overfitting. AdaBoost is simpler to implement and can be effective in certain scenarios, especially when weak learners are prone to high bias.

Boosting methods like AdaBoost and Gradient Boosting represent a significant advancement in ensemble learning techniques. By sequentially training weak learners and focusing on difficult instances, boosting effectively reduces bias and improves model accuracy. The mathematical formulations provide a solid foundation for understanding how these algorithms operate and how they can be optimized for various machine learning tasks

6.5. Advanced Ensemble Techniques link

In the evolution of boosting methods, advanced techniques like XGBoost, LightGBM, and CatBoost have become dominant in industry due to their speed, scalability, and ability to handle large datasets and complex feature spaces. These methods build on the fundamental principles of boosting, as seen in AdaBoost and Gradient Boosting, while introducing significant optimizations that make them practical for real-world applications with big data.

XGBoost, LightGBM, and CatBoost are extensions of the traditional Gradient Boosting framework. These algorithms enhance the original boosting approach by optimizing for both computational efficiency and predictive performance. Their core idea is to build an ensemble of decision trees, with each new tree focusing on correcting the errors of the previous trees, following the boosting principle. However, they introduce improvements in how the trees are built, how data is processed, and how the algorithms interact with modern hardware.

XGBoost, or Extreme Gradient Boosting, was one of the earliest and most popular advanced boosting algorithms. It implements several key optimizations, such as regularization to prevent overfitting, efficient handling of sparse data, and parallelized tree building. The algorithm uses second-order derivatives (Hessian information) of the loss function, which allows for more accurate gradient updates and faster convergence.

LightGBM, developed by Microsoft, further improves on XGBoost by introducing a novel approach to tree construction called Gradient-Based One-Side Sampling (GOSS) and Exclusive Feature Bundling (EFB). GOSS reduces the computational cost by selecting a subset of data points with large gradients, which contributes more to the learning process, while EFB groups mutually exclusive features to reduce dimensionality. This results in faster training times and the ability to scale to very large datasets with millions of instances and features.

CatBoost, developed by Yandex, is specifically optimized for handling categorical features. Traditional boosting methods often require manual preprocessing of categorical features through encoding techniques like one-hot encoding. In contrast, CatBoost introduces a method that directly handles categorical features during the training process, reducing the need for extensive preprocessing. Additionally, CatBoost implements techniques like ordered boosting to avoid prediction shift and is designed to work efficiently on distributed systems.

XGBoost, LightGBM, and CatBoost bring several conceptual improvements over traditional boosting methods. One of the most significant advancements is their ability to handle sparse and large-scale data efficiently. In XGBoost, sparsity is handled using a sparsity-aware algorithm, which allows the model to skip missing values during tree construction, thereby reducing computational complexity. XGBoost also incorporates regularization terms into the objective function to penalize model complexity, which helps in controlling overfitting.

Mathematically, the objective function in XGBoost is defined as:

$$ \mathcal{L}(\theta) = \sum_{i=1}^n L(y_i, \hat{y}_i) + \sum_{k=1}^T \Omega(f_k), $$

where $L(y_i, \hat{y}_i)$ is the loss function, and $\Omega(f_k)$ is the regularization term for the complexity of the $k$-th tree. The regularization term is designed to control the depth of the trees and the number of leaves, ensuring that the model does not overfit the training data.

LightGBM introduces GOSS, which improves computational efficiency by focusing on instances with higher gradients. This approach works by sampling a small subset of instances with small gradients and a larger subset of instances with large gradients, thereby ensuring that the model focuses on correcting the most significant errors while still learning from a representative portion of the data. EFB reduces the feature space by bundling mutually exclusive features, which optimizes memory usage and further reduces the computational complexity.

CatBoost addresses one of the primary challenges in machine learning: dealing with categorical features. In traditional methods, categorical features are usually transformed into numerical values through methods like one-hot encoding, which can lead to high-dimensional datasets. CatBoost introduces a novel approach by converting categorical values into numerical values using target-based statistics while avoiding data leakage. CatBoost also uses ordered boosting to ensure that during training, the model does not use future information for predicting past instances, which helps prevent overfitting.

Another critical conceptual improvement in these advanced boosting algorithms is their ability to leverage parallel processing and distributed systems. XGBoost was one of the first algorithms to implement parallelized tree construction by using a block-based structure that enables data to be processed independently across different cores. LightGBM also supports parallel learning by dividing the dataset into multiple smaller chunks, which can be processed simultaneously, making it highly scalable for large datasets. CatBoost introduces GPU support and distributed training, further enhancing its performance on high-dimensional and large-scale data.

Incorporating advanced boosting techniques like XGBoost, LightGBM, and CatBoost into a Rust-based machine learning workflow can be achieved through Foreign Function Interface (FFI) or Rust bindings. These algorithms are typically implemented in high-performance languages such as C++ for efficiency, and Rust offers the ability to integrate these implementations seamlessly using FFI, allowing Rust-based applications to leverage the performance benefits of these algorithms.

The xgboost crate provides Rust bindings for the XGBoost library, enabling developers to use XGBoost within Rust applications. To implement XGBoost in Rust, one can initialize the dataset, specify the objective function and hyperparameters, train the model, and make predictions using the XGBoost API. The flexibility of Rust’s type system and memory safety guarantees, combined with the efficiency of XGBoost, makes it a compelling choice for production-level machine learning systems.

use xgboost::{parameters, DMatrix, Booster};

fn main() {
    // training matrix with 5 training examples and 3 features
    let x_train = &[1.0, 1.0, 1.0,
                    1.0, 1.0, 0.0,
                    1.0, 1.0, 1.0,
                    0.0, 0.0, 0.0,
                    1.0, 1.0, 1.0];
    let num_rows = 5;
    let y_train = &[1.0, 1.0, 1.0, 0.0, 1.0];

    // convert training data into XGBoost's matrix format
    let mut dtrain = DMatrix::from_dense(x_train, num_rows).unwrap();

    // set ground truth labels for the training matrix
    dtrain.set_labels(y_train).unwrap();

    // test matrix with 1 row
    let x_test = &[0.7, 0.9, 0.6];
    let num_rows = 1;
    let y_test = &[1.0];
    let mut dtest = DMatrix::from_dense(x_test, num_rows).unwrap();
    dtest.set_labels(y_test).unwrap();

    // specify datasets to evaluate against during training
    let evaluation_sets = &[(&dtrain, "train"), (&dtest, "test")];

    // specify overall training setup
    let training_params = parameters::TrainingParametersBuilder::default()
        .dtrain(&dtrain)
        .evaluation_sets(Some(evaluation_sets))
        .build()
        .unwrap();

    // train model, and print evaluation data
    let bst = Booster::train(&training_params).unwrap();

    println!("{:?}", bst.predict(&dtest).unwrap());
}

For LightGBM, Rust bindings can be used to integrate LightGBM’s capabilities with Rust projects. The steps involved in integrating LightGBM include loading the dataset, configuring the model’s hyperparameters (such as learning rate, number of iterations, and maximum depth), and training the model using LightGBM’s efficient tree-building algorithms. LightGBM’s focus on speed and scalability makes it ideal for applications that require real-time predictions or need to handle very large datasets.

use lightgbm::{Dataset, Booster};
use serde_json::json;

let data = vec![vec![1.0, 0.1, 0.2, 0.1],
               vec![0.7, 0.4, 0.5, 0.1],
               vec![0.9, 0.8, 0.5, 0.1],
               vec![0.2, 0.2, 0.8, 0.7],
               vec![0.1, 0.7, 1.0, 0.9]];
let label = vec![0.0, 0.0, 0.0, 1.0, 1.0];
let dataset = Dataset::from_mat(data, label).unwrap();
let params = json!{
   {
        "num_iterations": 3,
        "objective": "binary",
        "metric": "auc"
    }
};
let bst = Booster::train(dataset, &params).unwrap();

CatBoost can also be integrated into Rust-based applications through FFI. CatBoost’s native support for handling categorical features and its efficient use of GPUs and distributed systems makes it highly suitable for tasks involving high-dimensional categorical data, such as recommendation systems or fraud detection. The workflow for using CatBoost in Rust would involve configuring the categorical feature handling, specifying the loss function, and setting up the training process. Tuning hyperparameters such as the learning rate, depth of the trees, and number of iterations is essential for optimizing the model’s performance on large datasets.

use catboost_rs as catboost;

fn main() {
    // Load the trained model
    let model = catboost::Model::load("tmp/model.bin").unwrap();

    println!("Number of cat features {}", model.get_cat_features_count());
    println!("Number of float features {}", model.get_float_features_count());

    // Apply the model
    let prediction = model
        .calc_model_prediction(
            vec![
                vec![-10.0, 5.0, 753.0],
                vec![30.0, 1.0, 760.0],
                vec![40.0, 0.1, 705.0],
            ],
            vec![
                vec![String::from("north")],
                vec![String::from("south")],
                vec![String::from("south")],
            ],
        )
        .unwrap();
    println!("Prediction {:?}", prediction);
}

When working with large datasets, it is crucial to tune the hyperparameters of these algorithms to achieve optimal performance. For example, the learning rate, number of iterations, and tree depth are critical factors that influence both the accuracy and the speed of the models. Cross-validation techniques can be used to assess the performance of the model on validation data, allowing for a systematic search for the best combination of hyperparameters.

In practice, XGBoost, LightGBM, and CatBoost are often compared based on their performance on specific tasks and datasets. XGBoost is known for its versatility and strong regularization capabilities, making it suitable for tasks where overfitting is a concern. LightGBM excels in handling very large datasets efficiently, making it ideal for applications in industries like finance and healthcare. CatBoost is particularly effective when dealing with datasets that have many categorical features, as it eliminates the need for extensive feature engineering.

These algorithms can be applied in various real-world scenarios, such as customer churn prediction, fraud detection, recommendation systems, and financial forecasting. Their ability to handle complex data types, combined with their scalability and efficiency, makes them indispensable tools in modern machine learning pipelines.

XGBoost, LightGBM, and CatBoost represent significant advancements in boosting algorithms, addressing key challenges such as scalability, speed, and handling categorical data. By building on the fundamental ideas of traditional boosting methods like AdaBoost and Gradient Boosting, these advanced techniques offer more efficient and powerful solutions for large-scale machine learning tasks. The improvements they bring in terms of computational efficiency, handling sparse and categorical data, and leveraging parallel processing make them widely used across industries that require fast and accurate predictions.

Incorporating these advanced ensemble techniques into Rust-based machine learning projects through FFI or Rust bindings allows developers to take advantage of their performance benefits while maintaining Rust’s memory safety and concurrency features. By tuning hyperparameters and carefully analyzing the performance of these models on large datasets, practitioners can leverage the strengths of XGBoost, LightGBM, and CatBoost to solve a wide range of predictive modeling problems effectively.

6.7. Conclusion link

Chapter 6 provides a deep dive into decision trees and ensemble methods, offering both theoretical insights and practical tools for implementation in Rust. By mastering these techniques, you will be well-equipped to tackle a wide range of machine learning challenges with robust and interpretable models.

6.7.1. Further Learning with GenAI link

Each prompt is intended to help you understand the underlying theory, apply it in Rust, and critically analyze the results.

• Explain the fundamental principles of decision trees. How do decision trees split data based on features, and what are the criteria used to evaluate splits (e.g., Gini impurity, information gain)? Implement a decision tree from scratch in Rust.

• Discuss the problem of overfitting in decision trees. How does overfitting occur, and what techniques can be used to mitigate it, such as pruning and regularization? Implement pre-pruning and post-pruning techniques in Rust, and compare their effectiveness.

• Analyze the concept of Gini impurity and information gain in decision trees. How do these criteria influence the splits made by the tree, and what are the trade-offs between them? Implement both criteria in Rust and apply them to different datasets.

• Explore the trade-offs between tree depth and model complexity in decision trees. How does increasing tree depth affect the model's performance and risk of overfitting? Implement a decision tree in Rust and experiment with different maximum depths to analyze the impact.

• Discuss the concept of feature importance in decision trees. How is feature importance calculated, and why is it valuable in understanding model behavior? Implement feature importance analysis in Rust for a decision tree model.

• Explain the principles of ensemble methods, particularly bagging and Random Forests. How does combining multiple decision trees into an ensemble reduce variance and improve model robustness? Implement a Random Forest algorithm in Rust and analyze its performance.

• Discuss the concept of bootstrap sampling and out-of-bag error in Random Forests. How do these techniques contribute to the effectiveness of Random Forests? Implement bootstrap sampling and out-of-bag error estimation in Rust, and apply them to a Random Forest model.

• Analyze the role of feature randomness in Random Forests. How does selecting a random subset of features for each split help reduce overfitting and increase model diversity? Implement feature randomness in Rust and experiment with different settings on a dataset.

• Explore the differences between bagging and boosting as ensemble techniques. How do these methods address variance and bias, respectively, and what are their relative strengths and weaknesses? Implement both bagging and boosting in Rust and compare their performance.

• Discuss the principles of AdaBoost and Gradient Boosting. How do these boosting methods iteratively adjust weights to focus on misclassified instances? Implement AdaBoost and Gradient Boosting algorithms in Rust, and apply them to classification problems.

• Analyze the concept of learning rate in boosting algorithms. How does the learning rate affect the convergence and performance of Gradient Boosting? Experiment with different learning rates in Rust and analyze their impact on model accuracy.

• Explore the use of regularization in boosting algorithms. How does regularization help prevent overfitting in models like Gradient Boosting, and what are the common regularization techniques used? Implement regularization in a Gradient Boosting model in Rust.

• Discuss the advancements made by XGBoost, LightGBM, and CatBoost over traditional boosting methods. How do these methods handle categorical features, sparse data, and parallel processing? Implement one of these advanced boosting methods in Rust and analyze its performance on a large dataset.

• Analyze the importance of hyperparameter tuning in ensemble methods. How do parameters like the number of trees, maximum depth, and learning rate affect the performance of Random Forests and boosting models? Implement hyperparameter tuning for an ensemble method in Rust and evaluate the results.

• Discuss the interpretability of ensemble models, particularly Random Forests and boosting methods. How can techniques like feature importance and SHAP values be used to understand and explain model predictions? Implement interpretability techniques in Rust for an ensemble model.

• Explore the concept of out-of-bag error in Random Forests. How is out-of-bag error calculated, and why is it a useful estimate of model accuracy? Implement out-of-bag error estimation in Rust and compare it to cross-validation results.

• Discuss the application of ensemble methods to imbalanced datasets. How can techniques like Random Forests and boosting be adapted to handle class imbalance, and what are the challenges involved? Implement an ensemble method in Rust for an imbalanced dataset and analyze its performance.

• Analyze the scalability of ensemble methods like Random Forests and XGBoost. How do these methods handle large datasets, and what are the computational challenges involved? Implement a scalable ensemble method in Rust and evaluate its performance on a large dataset.

• Explore the trade-offs between using a single, complex model (e.g., a deep neural network) versus an ensemble of simpler models. In what scenarios might an ensemble method be preferred, and how do ensemble methods achieve robustness and accuracy?

By engaging with these prompts, you will deepen your knowledge of how these powerful techniques work, how to implement them effectively, and how to critically evaluate their performance.

6.7.2. Hands-On Practices link

These exercises are designed to be challenging and in-depth, requiring you to apply both theoretical knowledge and practical skills in Rust.