7.1. Introduction to Support Vector Machines link

Support Vector Machines (SVMs) are a powerful class of supervised learning algorithms primarily used for classification tasks but can also be adapted for regression problems. The fundamental idea behind SVMs is to find a hyperplane that best separates the classes in a high-dimensional space. A hyperplane is a flat affine subspace of one dimension less than its ambient space; in two dimensions, it is a line, while in three dimensions, it is a plane. The goal of an SVM is to identify the optimal hyperplane that maximizes the margin between the classes. The margin is defined as the distance between the hyperplane and the nearest data points from either class, which are known as support vectors. By maximizing this margin, SVMs enhance the model's generalization capability, reducing the likelihood of overfitting.

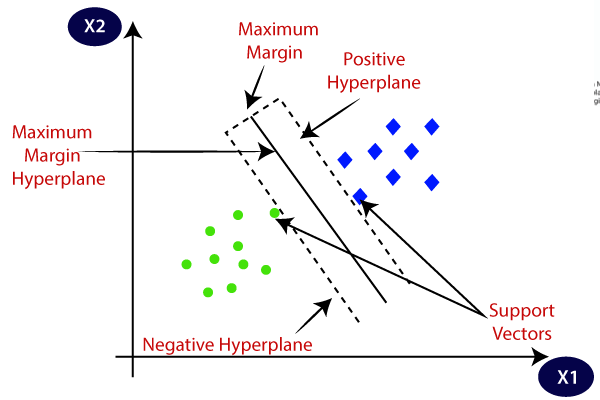
Figure 1: Main ideas of Support Vector Machine.

The decision boundary in SVMs is a crucial concept that determines how the model classifies new data points. When training the SVM, the algorithm seeks to identify the hyperplane that not only separates the classes but does so with the largest possible margin. This pursuit of margin maximization is what distinguishes SVMs from other classification methods. Conceptually, SVMs can be viewed as a method of finding the best line (or hyperplane) that divides the data points of one class from those of another, while also ensuring that the distance to the nearest points (the support vectors) is as large as possible. This characteristic is particularly important in high-dimensional spaces where the risk of overfitting is heightened, as a larger margin typically correlates with better model performance on unseen data.

Given a set of training data $\{(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\}$, where $x_i \in \mathbb{R}^d$ represents the feature vectors and $y_i \in \{-1, +1\}$ denotes the corresponding class labels, the objective of SVM is to find a hyperplane that divides the data points according to their class labels. Mathematically, a hyperplane in a $d$-dimensional space is described by the equation:

$$ w^T x + b = 0 $$

where $w \in \mathbb{R}^d$ is the normal vector to the hyperplane and $b \in \mathbb{R}$ is the bias or intercept term that shifts the hyperplane from the origin. The vector $w$ determines the orientation of the hyperplane, while $b$ determines its position in space. For any point $x_i$, the sign of $w^T x_i + b$ determines the class to which it belongs. If $w^T x_i + b > 0$, the point belongs to class $+1$; otherwise, it belongs to class $-1$.

The key idea in SVM is to select the hyperplane that maximizes the margin between the two classes. The margin is defined as the perpendicular distance from the hyperplane to the nearest points in either class, known as support vectors. The distance from a point xix_ixi to the hyperplane is given by:

$$ \frac{|w^T x_i + b|}{\|w\|} $$

The goal is to maximize this margin while ensuring that all points are correctly classified. This leads to the following optimization problem:

$$ \min_{w, b} \frac{1}{2} \|w\|^2w, $$

subject to the constraint that each data point is correctly classified:

$$ y_i (w^T x_i + b) \geq 1 \quad \forall i = 1, \dots, n $$

The objective function $\frac{1}{2} \|w\|^2$ is minimized to maximize the margin. Minimizing $\|w\|$ makes the hyperplane as far from the closest points as possible, which enhances the model's generalization ability. The constraints $y_i (w^T x_i + b) \geq 1$ ensure that the data points are correctly classified with a margin of at least 1. This is known as a hard-margin SVM, where the assumption is that the data is linearly separable.

The optimization problem can be tackled using the method of Lagrange multipliers. Introducing Lagrange multipliers $\alpha_i \geq 0$ for each constraint, the Lagrangian function is defined as:

$$ L(w, b, \alpha) = \frac{1}{2} \|w\|^2 - \sum_{i=1}^{n} \alpha_i \left[ y_i (w^T x_i + b) - 1 \right] $$

The primal optimization problem can be transformed into its dual form by maximizing the Lagrangian with respect to $w$ and $b$. The dual problem is given by:

$$ \max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j x_i^T x_j $$

subject to the constraints:

$$ \sum_{i=1}^{n} \alpha_i y_i = 0, \quad \alpha_i \geq 0i=1 $$

The solution to this dual problem yields the values of the Lagrange multipliers $\alpha_i$, which define the support vectors. Only those points with $\alpha_i > 0$ are support vectors; these are the points that lie on the margin.

Once the optimal values of $\alpha_i$ are determined, the optimal hyperplane can be expressed as a linear combination of the support vectors:

$$ w = \sum_{i=1}^{n} \alpha_i y_i x_i $$

The decision function for a new test point $x$ is given by:

$$ f(x) = \text{sign} \left( \sum_{i=1}^{n} \alpha_i y_i x_i^T x + b \right) $$

This function determines whether the point $x$ belongs to class $+1$ or $-1$.

In cases where the data is not perfectly separable, SVM can be extended to handle such scenarios using the soft-margin approach. The idea is to allow for some misclassification by introducing slack variables $\xi_i \geq 0$ for each data point. The modified optimization problem is:

$$ \min_{w, b, \xi} \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{n} \xi_iw, $$

subject to the constraints:

$$ y_i (w^T x_i + b) \geq 1 - \xi_i \quad \forall i = 1, \dots, n $$

where $C > 0$ is a regularization parameter that controls the trade-off between maximizing the margin and minimizing classification errors.

For data that is not linearly separable in the input space, SVM can use a kernel function to map the data into a higher-dimensional feature space where linear separation is possible. The kernel function $K(x_i, x_j)$ computes the dot product between the images of the input vectors $x_i$ and $x_j$ in the feature space. Commonly used kernels include:

• Polynomial kernel: $K(x_i, x_j) = (x_i^T x_j + 1)^d$

• Radial Basis Function (RBF) kernel: $K(x_i, x_j) = \exp \left( -\frac{\|x_i - x_j\|^2}{2 \sigma^2} \right)$

The dual formulation of the SVM is modified to incorporate the kernel function:

$$ \max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j K(x_i, x_j) $$

To implement a basic SVM from scratch in Rust, we can utilize libraries such as smartcore, which provide a robust framework for machine learning tasks. Below, we present a simple example of applying SVMs to a binary classification problem using Rust. First, we need to add smartcore to our Cargo.toml file:

[dependencies]
smartcore = "0.3.2"
rand = "0.8"

Next, we can create a basic implementation of SVM using the smartcore library. In this example, we will generate a synthetic dataset and fit an SVM model to classify the data points.

use smartcore::linalg::basic::matrix::DenseMatrix;
use smartcore::svm::svc::{SVC, SVCParameters};
use smartcore::dataset::iris::load_dataset;
use smartcore::svm::LinearKernel;
use rand::seq::SliceRandom;
use rand::thread_rng;

fn main() {
    // Load the Iris dataset, which is a common benchmark dataset for classification
    let iris = load_dataset();

    // Split the dataset into data and target
    let (data, target) = (iris.data, iris.target);

    // The Iris dataset has 150 samples with 4 features each, so we need to reshape
    let columns = 4; // Number of features per sample

    // Convert the flat data into a Vec<Vec<f64>>
    let binary_data: Vec<Vec<f64>> = data
        .chunks(columns)
        .map(|chunk| chunk.iter().map(|&x| x as f64).collect())
        .collect();

    // Filter the binary target to use only class 0 and class 1
    let binary_data_filtered: Vec<Vec<f64>> = binary_data
        .iter()
        .zip(target.iter())
        .filter(|(_, &label)| label == 0 || label == 1)
        .map(|(row, _)| row.clone())
        .collect();

    let binary_target: Vec<i32> = target
        .iter()
        .filter(|&&label| label == 0 || label == 1)
        .map(|&label| if label == 0 { -1 } else { 1 }) // Change labels from 0, 1 to -1, 1
        .collect();

    // Shuffle data and labels together
    let mut rng = thread_rng();
    let mut combined: Vec<_> = binary_data_filtered.iter().zip(binary_target.iter()).collect();
    combined.shuffle(&mut rng);

    // Create new variables for filtered data and target after shuffling
    let shuffled_data: Vec<Vec<f64>> = combined.iter().map(|(x, _)| (*x).clone()).collect();
    let shuffled_target: Vec<i32> = combined.iter().map(|(_, &y)| y).collect();

    // Split data into training and testing sets
    let split_index = (0.8 * shuffled_data.len() as f64).round() as usize;
    let (train_data, test_data) = shuffled_data.split_at(split_index);
    let (train_target, test_target) = shuffled_target.split_at(split_index);

    // Convert train_data to a DenseMatrix for training
    let train_matrix = DenseMatrix::from_2d_vec(&train_data.to_vec());
    let test_matrix = DenseMatrix::from_2d_vec(&test_data.to_vec());

    // Store the train_target as a vector
    let train_target_vec = train_target.to_vec();

    // Create the SVM model with appropriate parameters
    let params = SVCParameters::default()
        .with_c(1.0)
        .with_kernel(LinearKernel);  // Use LinearKernel

    // Train the SVM model on the training data
    let svm = SVC::fit(&train_matrix, &train_target_vec, &params)
        .expect("Failed to fit the SVM model.");

    // Make predictions on the test data
    let predictions = svm
        .predict(&test_matrix)
        .expect("Failed to make predictions.");

    // Output the predictions for review
    for (true_label, pred) in test_target.iter().zip(predictions.iter()) {
        println!("True label: {}, Predicted: {}", true_label, pred);
    }
}

In this code, we begin by loading the Iris dataset, filtering it to include only two classes to simplify our binary classification task. We then create the SVM model, specifying the linear kernel, and fit it to our filtered dataset. Finally, we make predictions and print the results. This implementation serves as a straightforward introduction to using SVMs in Rust, showcasing how to leverage a machine learning library effectively.

7.2. Mathematical Foundation of SVMs link

Support Vector Machines (SVMs) are rooted in rigorous mathematical principles, particularly in optimization theory, convex optimization, and duality. At the heart of SVMs lies the task of finding a hyperplane that separates two classes while maximizing the margin between them. This section delves into the mathematical formulation of SVMs, focusing on the optimization problem that SVMs solve, the dual formulation, and the conditions under which the solution is derived.

The SVM classification task begins with a dataset $\{(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\}$, where $x_i \in \mathbb{R}^d$ represents the feature vectors, and $y_i \in \{-1, +1\}$ represents the corresponding class labels. The goal is to find a hyperplane defined by the equation $w^T x + b = 0$, where www is the normal vector to the hyperplane, and bbb is the bias term that shifts the hyperplane.

The problem of determining the optimal hyperplane is formulated as an optimization problem. Specifically, we aim to minimize the norm of the weight vector www, which maximizes the margin between the hyperplane and the nearest data points of each class (the support vectors). The optimization problem can be written as:

$$ \min_{w, b} \frac{1}{2} \|w\|^2w, $$

subject to the constraints that each data point is correctly classified:

$$ y_i (w^T x_i + b) \geq 1 \quad \forall i = 1, \dots, n $$

This is a convex optimization problem because the objective function $\frac{1}{2} \|w\|^2$ is quadratic, and the constraints are linear. Convex optimization ensures that any local minimum is also a global minimum, which is crucial for the efficiency and correctness of the SVM algorithm.

To solve this constrained optimization problem, we introduce the method of Lagrange multipliers, a technique used to convert a constrained problem into an unconstrained one. For each constraint $y_i (w^T x_i + b) \geq 1$, we introduce a non-negative Lagrange multiplier αi\\alpha_iαi. The Lagrangian function is then defined as:

$$ L(w, b, \alpha) = \frac{1}{2} \|w\|^2 - \sum_{i=1}^{n} \alpha_i \left[ y_i (w^T x_i + b) - 1 \right] $$

The Lagrange multipliers αi\\alpha_iαi ensure that the constraints are satisfied. The objective is now to minimize the Lagrangian with respect to $w$ and $b$, while maximizing it with respect to $\alpha$. The optimal solution must satisfy the following conditions:

• Stationarity: The gradient of the Lagrangian with respect to $w$ and $b$ must be zero.

• Primal feasibility: The original constraints $y_i (w^T x_i + b) \geq 1$ must hold.

• Dual feasibility: The Lagrange multipliers $\alpha_i \geq 0$ must be non-negative.

• Complementary slackness: $\alpha_i \left[ y_i (w^T x_i + b) - 1 \right] = 0$ for all $i$, which implies that either $\alpha_i = 0$ or the point $x_i$ lies on the margin.

These conditions are collectively known as the Karush-Kuhn-Tucker (KKT) conditions, and they play a critical role in deriving the SVM solution.

The dual formulation of the SVM problem is derived by solving the Lagrangian. The first step is to eliminate the primal variables $w$ and $b$ by setting the derivatives of $L(w, b, \alpha)$ with respect to $w$ and $b$ to zero. The derivative with respect to www gives:

$$ \frac{\partial L}{\partial w} = w - \sum_{i=1}^{n} \alpha_i y_i x_i = 0 $$

which implies that:

$$ w = \sum_{i=1}^{n} \alpha_i y_i x_i $$

This expression shows that the optimal weight vector $w$ is a linear combination of the training data points, where the coefficients are the Lagrange multipliers $\alpha_i$. Only the data points with $\alpha_i > 0$ (the support vectors) contribute to the solution.

Substituting this expression for $w$ into the Lagrangian gives the dual objective function, which depends only on the Lagrange multipliers αi\\alpha_iαi:

$$ \max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j x_i^T x_j $$

subject to the constraints:

$$\sum_{i=1}^{n} \alpha_i y_i = 0 \quad \text{and} \quad \alpha_i \geq 0 \quad \forall ii=1$$

This dual formulation is a quadratic programming problem, and it is often easier to solve than the primal problem, especially for large datasets.

Once the optimal values of the Lagrange multipliers αi\\alpha_iαi are found, the bias term bbb can be computed using the fact that for any support vector xix_ixi, the following condition must hold:

$$y_i (w^T x_i + b) = 1$$

Thus, the bias term can be computed as:

$$ b = y_i - \sum_{j=1}^{n} \alpha_j y_j x_j^T x_i $$

for any support vector $x_i$.

In practice, solving the SVM optimization problem involves numerical techniques, particularly for solving the quadratic programming problem that arises from the dual formulation. In Rust, this can be done using optimization libraries such as nalgebra for linear algebra operations and quadprog for quadratic programming.

Here is a basic implementation of solving the SVM dual problem in Rust using numerical optimization techniques:

use nalgebra::{DMatrix, DVector};
use quadprog::quadprog;

fn main() {
    // Define a simple dataset
    let x = DMatrix::from_row_slice(6, 2, &[
        1.0, 2.0,
        2.0, 3.0,
        3.0, 3.0,
        4.0, 5.0,
        1.0, 0.0,
        2.0, 1.0
    ]);
    let y = DVector::from_row_slice(&[1.0, 1.0, 1.0, 1.0, -1.0, -1.0]);

    // Compute the Gram matrix (K(x_i, x_j) = x_i^T x_j)
    let gram_matrix = x.clone() * x.transpose();

    // Set up the quadratic programming problem
    let p = gram_matrix.component_mul(&y * y.transpose());
    let q = -DVector::from_element(x.nrows(), 1.0);
    let g = DMatrix::from_element(x.nrows(), x.nrows(), -1.0);
    let h = DVector::from_element(x.nrows(), 0.0);

    // Solve the quadratic programming problem
    let result = quadprog::solve_qp(p, q, g, h);
    
    match result {
        Ok(solution) => {
            let alphas = solution.0;
            println!("Lagrange multipliers: {:?}", alphas);
        }
        Err(e) => {
            println!("Optimization failed: {:?}", e);
        }
    }
}

In this implementation, we use nalgebra for matrix operations and quadprog for solving the quadratic programming problem. The matrix p is the Gram matrix, which represents the dot products between the feature vectors weighted by the class labels. The vector q corresponds to the linear part of the dual objective function. The optimization yields the values of the Lagrange multipliers αi\\alpha_iαi, which define the support vectors.

The mathematical foundation of SVMs is deeply rooted in convex optimization, duality, and the KKT conditions. The formulation of the optimization problem, both in its primal and dual forms, allows SVMs to find the optimal hyperplane that separates classes while maximizing the margin. The use of Lagrange multipliers and the dual formulation provides a powerful framework for solving the SVM problem efficiently. Implementing this framework in Rust requires numerical optimization techniques, such as quadratic programming, to solve the underlying optimization problem and apply it to real-world classification tasks.

7.3. Kernel Trick and Non-Linear SVMs link

Support Vector Machines (SVMs) are powerful tools for binary classification, and their strength comes from their ability to construct decision boundaries that separate data points belonging to different classes. However, one limitation of the standard (linear) SVM is that it can only separate linearly separable data. Real-world data, however, often exhibits complex, non-linear patterns that cannot be separated by a single hyperplane. The kernel trick is a mathematical technique that extends SVMs to handle non-linearly separable data by implicitly mapping the input data into a higher-dimensional space where a linear separation may become feasible. This section explores the mathematical foundation of the kernel trick, various types of kernels, and the practical implementation of kernelized SVMs in Rust.

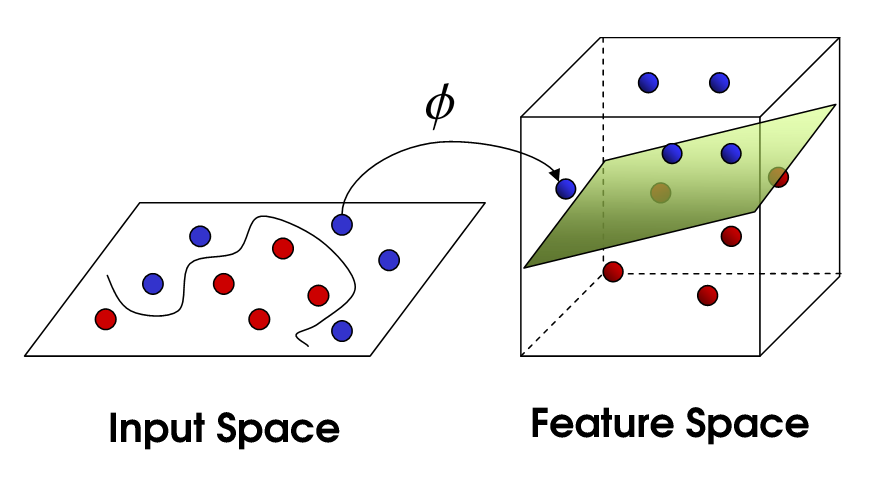
Figure 2: Kernel trick for SVM.

The kernel trick allows SVMs to operate in a higher-dimensional feature space without explicitly computing the transformation of data points into that space. Instead of mapping each point into a higher-dimensional space and computing the dot product between the transformed vectors, the kernel trick computes the dot product in the higher-dimensional space directly using a kernel function.

Let $\phi(x)$ represent a mapping from the input space $\mathbb{R}^d$ to a higher-dimensional space $\mathbb{R}^{d'}$, where $d' > d$. The SVM optimization problem in the higher-dimensional space becomes:

$$ w = \sum_{i=1}^{n} \alpha_i y_i \phi(x_i) $$

where $\alpha_i$ are the Lagrange multipliers, $y_i$ are the class labels, and $\phi(x_i)$ is the mapped version of the input vector $x_i$. In the higher-dimensional space, we want to compute the decision function:

$$ f(x) = \text{sign} \left( \sum_{i=1}^{n} \alpha_i y_i \phi(x_i)^T \phi(x) + b \right) $$

However, explicitly computing $\phi(x)$ and the dot products in the higher-dimensional space can be computationally expensive, especially when $d'$ is very large or infinite. The kernel trick avoids this direct computation by using a kernel function $K(x_i, x_j)$, which computes the dot product in the transformed space implicitly:

$$ K(x_i, x_j) = \phi(x_i)^T \phi(x_j) $$

This means we do not need to explicitly compute $\phi(x)$; instead, we can directly apply the kernel function to the original data points in the lower-dimensional input space. The dual formulation of the SVM problem becomes:

$$ \max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j K(x_i, x_j) $$

subject to the constraints:

$$ \sum_{i=1}^{n} \alpha_i y_i = 0, \quad \alpha_i \geq 0i=1 $$

Thus, the kernel function allows SVMs to construct non-linear decision boundaries in the original input space while performing the optimization in a higher-dimensional feature space. The kernel trick makes SVMs highly versatile for handling complex, non-linear classification problems.

The choice of the kernel function is critical in determining the performance of the SVM on non-linearly separable data. Different kernels map the input data into different types of feature spaces, and each kernel is suited for specific kinds of data structures and relationships. Some of the most common kernel functions used in SVMs are:

• Linear Kernel: The simplest kernel is the linear kernel, which corresponds to no mapping at all (i.e., the identity map). The kernel function is: $K(x_i, x_j) = x_i^T x_j$ . This kernel is equivalent to the standard linear SVM and is used when the data is linearly separable in the input space.

• Polynomial Kernel: The polynomial kernel maps the input data to a higher-dimensional space using polynomials of a certain degree. The kernel function is: $K(x_i, x_j) = (x_i^T x_j + c)^d$, where $c$ is a constant and $d$ is the degree of the polynomial. This kernel is effective for data that has polynomial relationships between features.

• Radial Basis Function (RBF) Kernel: Also known as the Gaussian kernel, the RBF kernel maps the input data to an infinite-dimensional space. The kernel function is: $K(x_i, x_j) = \exp \left( -\frac{\|x_i - x_j\|^2}{2 \sigma^2} \right)$, where $\sigma$ is a parameter that controls the spread of the kernel. The RBF kernel is widely used because it is versatile and can handle a wide variety of non-linear relationships.

• Sigmoid Kernel: The sigmoid kernel is inspired by neural networks and computes the kernel as: $K(x_i, x_j) = \tanh (\kappa x_i^T x_j + c)$, where $\kappa$ and $c$ are parameters. This kernel mimics the activation function of a neural network and can be used for classification tasks where the decision boundary follows a sigmoid curve.

Each kernel function transforms the input data into a different feature space, and the choice of kernel depends on the structure of the data. For instance, the RBF kernel is often used when the relationship between the features is highly non-linear, while the polynomial kernel is used when the data has polynomial trends.

To implement SVMs with different kernel functions in Rust, we can utilize libraries such as smartcore and linfa-svm, which provide built-in support for kernelized SVMs. In this example, we will use the linfa framework to implement kernelized SVMs and experiment with different kernel functions.

Example: Kernelized SVM using linfa link

Here is a Rust implementation of SVM with an RBF kernel using the linfa crate:

use linfa::prelude::*;
use linfa_svm::{Svm, SvmParams};
use ndarray::array;

fn main() {
    // Define a simple dataset with non-linear separation
    let data = array![
        [0.0, 0.0],
        [1.0, 1.0],
        [0.0, 1.0],
        [1.0, 0.0],
        [2.0, 2.0],
        [3.0, 3.0]
    ];
    let targets = array![1, 1, -1, -1, 1, -1];

    // Define SVM model with RBF kernel
    let model = SvmParams::new()
        .gaussian_kernel(1.0) // RBF kernel with sigma = 1.0
        .fit(&Dataset::new(data.view(), targets.view()))
        .expect("Failed to train model");

    // Predict on new data points
    let test_data = array![[0.5, 0.5], [2.5, 2.5]];
    let predictions = model.predict(test_data.view());

    // Print predictions
    println!("Predictions: {:?}", predictions);
}

In this implementation, we define a dataset where the data points are not linearly separable, meaning a straight line cannot perfectly divide the classes. To address this, we create an SVM model using the linfa framework and apply the Radial Basis Function (RBF) kernel, specified by gaussian_kernel(σ = 1.0), which maps the data into a higher-dimensional space where it becomes linearly separable. The model is trained using the fit method, which identifies the optimal support vectors and hyperplane in the transformed space. Once trained, the predict method is used to classify new data points, allowing the model to handle complex, non-linear decision boundaries effectively.

The kernel trick allows SVMs to handle non-linearly separable data by mapping it to a higher-dimensional space where linear separation becomes possible. This transformation is done implicitly through kernel functions, avoiding the computational cost of explicitly calculating the transformation. The choice of kernel function—linear, polynomial, RBF, or sigmoid—determines how the input space is transformed, and different kernels are suited to different kinds of data structures and relationships. Implementing kernelized SVMs in Rust is made easier by frameworks like linfa, which provide support for different kernel functions and allow experimentation with various models on non-linear datasets. This flexibility makes kernelized SVMs a powerful tool for handling complex classification tasks in a wide range of applications.

7.4. Support Vector Regression - SVR link

Support Vector Machines (SVMs) are commonly associated with classification tasks, but they can be extended to handle regression problems through a technique called Support Vector Regression (SVR). Just as SVMs attempt to find an optimal hyperplane that separates classes in classification, SVR seeks to find a function that best fits the training data while maintaining certain properties like robustness to outliers. This section introduces the mathematical foundation of SVR, explains its core conceptual ideas, and demonstrates its practical implementation in Rust.

In the context of regression, the goal is to predict continuous values rather than discrete class labels. Traditional regression techniques, such as linear regression, minimize the squared error between the predicted and actual values. SVR, on the other hand, employs a different strategy by focusing on approximating a function with a tolerance for error, known as the epsilon-insensitive loss function.

Given a dataset $\{(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\}$, where $x_i \in \mathbb{R}^d$ are the feature vectors and $y_i \in \mathbb{R}$ are the continuous target values, SVR aims to find a function $f(x) = w^T x + b$ that deviates from the actual target $y_i$ by at most a value $\epsilon$, while penalizing deviations larger than $\epsilon$.

The optimization problem for SVR can be written as:

$$ \min_{w, b, \xi, \xi^*} \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{n} (\xi_i + \xi_i^*)w, $$

subject to the constraints:

$$ y_i - w^T x_i - b \leq \epsilon + \xi_i $$

$$ w^T x_i + b - y_i \leq \epsilon + \xi_i^* $$

$$ \xi_i^* \geq 0 \quad \forall i $$

In this formulation, $\xi_i$ and $\xi_i^*$ are slack variables that allow for deviations beyond the $\epsilon$-insensitive zone, and $C$ is a regularization parameter that controls the trade-off between model complexity and the amount of allowed deviation beyond $\epsilon$. The term $\frac{1}{2} \|w\|^2$ ensures that the model minimizes the complexity (or maximizes the margin), while the second term $C \sum_{i=1}^{n} (\xi_i + \xi_i^*)$ penalizes the data points that lie outside the $\epsilon$-insensitive band.

One of the key differences between SVR and traditional regression methods is the use of the epsilon-insensitive loss function, which defines a margin of tolerance around the regression line. This margin allows SVR to ignore small errors as long as they lie within the $\epsilon$-band around the predicted value. The loss function for SVR is defined as:

$$ L_{\epsilon}(y, f(x)) = \begin{cases} 0 & \text{if } |y - f(x)| \leq \epsilon \\ |y - f(x)| - \epsilon & \text{otherwise} \end{cases} $$

This loss function ensures that predictions within the ϵ\\epsilonϵ-band do not contribute to the optimization objective, making SVR more robust to noise and minor fluctuations in the data.

The support vectors in SVR play a similar role to those in SVM classification. In SVR, the support vectors are the data points that lie either on the boundary of the ϵ\\epsilonϵ-insensitive band or outside of it (i.e., the points for which $\xi_i$ or $\xi_i^*$ are non-zero). These points define the regression function, and as with classification SVMs, the number of support vectors influences the complexity of the model.

Unlike traditional regression techniques that minimize squared errors across all data points, SVR focuses only on the support vectors, which are the most informative points in the dataset. As a result, SVR tends to produce sparse models that generalize well to unseen data.

Similar to SVMs for classification, SVR can be formulated in its dual form using Lagrange multipliers. The dual formulation allows the use of the kernel trick, enabling SVR to handle non-linear relationships in the data by implicitly mapping the input features into a higher-dimensional space.

The dual problem for SVR can be expressed as:

$$ \max_{\alpha, \alpha^*} \sum_{i=1}^{n} (\alpha_i^* - \alpha_i) y_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} (\alpha_i^* - \alpha_i)(\alpha_j^* - \alpha_j) K(x_i, x_j)α, $$

subject to the constraints:

$$ \sum_{i=1}^{n} (\alpha_i^* - \alpha_i) = 0 $$

$$ 0 \leq \alpha_i, \alpha_i^* \leq C $$

where $K(x_i, x_j)$ is a kernel function, such as the linear, polynomial, or radial basis function (RBF) kernel. The dual formulation leverages the kernel trick to map the input data into a higher-dimensional space, where linear SVR can be applied.

To implement Support Vector Regression in Rust, we can use libraries such as linfa or smartcore. Below is an example of how to implement SVR using the linfa crate:

Example: Support Vector Regression with Linfa link

use linfa::prelude::*;
use linfa_svm::Svm;
use linfa_svm::SvmParams;
use ndarray::array;

fn main() {
    // Define a simple dataset for regression
    let data = array![
        [0.0],
        [1.0],
        [2.0],
        [3.0],
        [4.0],
        [5.0],
        [6.0],
        [7.0]
    ];
    let targets = array![0.0, 0.8, 0.9, 0.1, 0.2, 0.8, 0.9, 1.0];

    // Define the SVR model with an RBF kernel
    let model = SvmParams::new()
        .gaussian_kernel(0.5) // RBF kernel with sigma = 0.5
        .epsilon(0.1) // epsilon-insensitive band of width 0.1
        .fit(&Dataset::new(data.view(), targets.view()))
        .expect("Failed to train SVR model");

    // Predict new values
    let test_data = array![[1.5], [3.5], [5.5]];
    let predictions = model.predict(test_data.view());

    // Output the predictions
    println!("Predictions: {:?}", predictions);
}

In this code, the dataset consists of single-dimensional input values representing a feature (such as time or distance) and continuous target values that we aim to predict. An SVR model is created using the SvmParams object from the linfa library, where we define an RBF kernel with $\sigma = 0.5$ and set an epsilon-insensitive loss function to ignore errors smaller than $\epsilon = 0.1$. The fit method trains the SVR model, identifying the support vectors and fitting a regression function that balances complexity with tolerance for small errors within the epsilon-insensitive zone. Once the model is trained, the predict method is used to estimate the target values for new input data, and the predictions are printed as output.

Support Vector Regression (SVR) extends the SVM framework to handle regression problems by introducing the epsilon-insensitive loss function. This function allows SVR to focus on data points that fall outside a specified margin of tolerance, resulting in a robust model that is less sensitive to noise and outliers. Unlike traditional regression techniques that minimize squared errors across all data points, SVR minimizes a loss function that penalizes only the points outside the ϵ\\epsilonϵ-band. This leads to sparser models defined by support vectors, which help to generalize well to unseen data. By leveraging the kernel trick, SVR can also model non-linear relationships in the data. Implementing SVR in Rust is straightforward with libraries like linfa, allowing experimentation with different kernel functions and hyperparameters for various regression tasks.

7.5. Soft Margin SVMs and Regularization link

In real-world scenarios, data is rarely perfectly separable. Traditional hard-margin Support Vector Machines (SVMs) assume that the data can be perfectly divided by a hyperplane, which is often unrealistic when dealing with noisy or overlapping data. To address this, soft margin SVMs introduce the concept of allowing some misclassification or error in the training set, enabling the model to handle non-separable datasets. The introduction of soft margin SVMs transforms the SVM optimization problem into one where the model seeks a balance between maximizing the margin and minimizing classification errors. This section explores the mathematical formulation of soft margin SVMs, the role of regularization, and the practical implementation of soft margin SVMs in Rust.

In the standard SVM formulation, we aim to find a hyperplane that separates the data points perfectly by maximizing the margin. The objective function for this hard-margin SVM is:

$$ \min_{w, b} \frac{1}{2} \|w\|^2w, $$

subject to the constraints:

$$ y_i (w^T x_i + b) \geq 1 \quad \forall i $$

However, when the data is not linearly separable, the constraints $y_i (w^T x_i + b) \geq 1$ cannot be satisfied for all data points. To account for this, soft margin SVMs introduce slack variables $xi_i \geq 0$, which allow some data points to violate the margin constraints. The optimization problem for soft margin SVMs becomes:

$$ \min_{w, b, \xi} \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{n} \xi_i $$

subject to the modified constraints:

$$ y_i (w^T x_i + b) \geq 1 - \xi_i \quad \forall i $$

$$ \xi_i \geq 0 \quad \forall i $$

The parameter $C$ is a regularization parameter that controls the trade-off between maximizing the margin and minimizing classification errors. The slack variables $\xi_i$ represent the amount by which the margin constraint is violated for each data point. If $\xi_i = 0$, the point lies on or outside the margin, but if $\xi_i > 0$, the point is either inside the margin or misclassified. The term $C \sum_{i=1}^{n} \xi_i$ penalizes misclassifications, and the parameter $C$ controls the degree of this penalty.

The introduction of slack variables and the regularization parameter $C$ fundamentally changes the behavior of the SVM model. In soft margin SVMs, the objective is no longer solely to maximize the margin but also to find a balance between margin maximization and error minimization. The value of $C$ determines how much weight is given to classification errors.

• High $C$: When $C$ is large, the model penalizes classification errors heavily, meaning it prioritizes correctly classifying as many points as possible, even at the expense of a smaller margin. This can lead to overfitting, where the model becomes too sensitive to noise in the data, as it tries to minimize the error for all points, including outliers.

• Low $C$: When $C$ is small, the model allows more misclassifications, leading to a larger margin. This results in a more robust model that generalizes better to unseen data, as it focuses on maximizing the margin rather than fitting every training point perfectly. However, if $C$ is too small, the model might underfit by allowing too many classification errors.

The trade-off between the margin size and classification error is an essential aspect of soft margin SVMs. The regularization parameter $C$ enables the model to handle noisy and non-separable data by allowing some degree of misclassification while maintaining the margin as large as possible.

The dual formulation of soft margin SVMs, which introduces Lagrange multipliers, remains similar to that of hard-margin SVMs but with modifications to account for the slack variables. The Lagrangian for the soft margin SVM can be written as:

$$ L(w, b, \alpha, \xi) = \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{n} \xi_i - \sum_{i=1}^{n} \alpha_i \left( y_i (w^T x_i + b) - 1 + \xi_i \right) $$

where $\alpha_i \geq 0$ are the Lagrange multipliers associated with the constraints. Solving the Lagrangian with respect to $w$ and $\xi$ leads to the following dual optimization problem:

$$ \max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j K(x_i, x_j) $$

subject to the constraints:

$$ \sum_{i=1}^{n} \alpha_i y_i = 0 \quad \text{and} \quad 0 \leq \alpha_i \leq C \quad \forall ii=1 $$

In the dual formulation, the kernel function $K(x_i, x_j)$ can be used to extend soft margin SVMs to non-linear data, making it possible to find non-linear decision boundaries.

To implement soft margin SVMs in Rust, we can use machine learning libraries such as linfa or smartcore. These libraries provide efficient implementations of SVMs with support for the soft margin formulation. Below is an example using the linfa framework to implement a soft margin SVM and experiment with different values of the regularization parameter $C$.

Example: Soft Margin SVM with Linfa link

use linfa::prelude::*;
use linfa_svm::{Svm, SvmParams};
use ndarray::array;

fn main() {
    // Define a non-separable dataset
    let data = array![
        [1.0, 2.0],
        [2.0, 3.0],
        [3.0, 3.0],
        [4.0, 5.0],
        [1.0, 0.0],
        [2.0, 1.0],
        [3.0, 1.0]
    ];
    let targets = array![1, 1, 1, 1, -1, -1, -1];

    // Define the SVM model with a soft margin and linear kernel
    let model = SvmParams::new()
        .linear_kernel()      // Use a linear kernel
        .c(1.0)              // Set the regularization parameter C
        .fit(&Dataset::new(data.view(), targets.view()))
        .expect("Failed to train SVM model");

    // Predict the class labels for new data points
    let test_data = array![[1.5, 1.5], [3.5, 4.0], [2.5, 2.5]];
    let predictions = model.predict(test_data.view());

    // Print predictions
    println!("Predictions: {:?}", predictions);
}

In this explanation, the dataset consists of two classes where the data is not perfectly separable, meaning some overlap between the classes is expected. We define a soft margin SVM using SvmParams from the linfa library, specifying a linear decision boundary with the linear_kernel() function. The regularization parameter $C = 1.0$ controls the trade-off between margin maximization and error minimization, and adjusting $C$ allows experimentation with different behaviors. The model is trained using the fit function, and predictions on new data points are made using the predict function, showing how the soft margin SVM handles the classification task. By varying $C$, we can influence the model’s behavior, where a higher $C$ forces more correct classifications but may shrink the margin, and a lower $C$ increases the margin but tolerates more classification errors.

Soft margin SVMs extend the basic SVM framework by allowing for misclassification in the training data, making them suitable for real-world datasets that are noisy or non-separable. The introduction of slack variables enables the model to tolerate violations of the margin constraints, while the regularization parameter $C$ controls the trade-off between margin maximization and classification error minimization. By adjusting $C$, we can tune the model's behavior to handle varying levels of noise and complexity in the data. Soft margin SVMs offer a powerful tool for classification tasks where the data is not perfectly separable, and implementing them in Rust is facilitated by libraries like linfa and smartcore.

7.6. Model Evaluation and Hyperparameter Tuning link

Support Vector Machines (SVMs) are powerful and versatile models for classification and regression tasks. However, achieving optimal performance with SVMs requires careful evaluation and fine-tuning of hyperparameters. This section provides an in-depth explanation of the importance of evaluating SVM models, discusses various evaluation metrics, and covers techniques for hyperparameter tuning such as grid search and random search.

Evaluating an SVM model is crucial to ensure that it generalizes well to unseen data. An SVM with inappropriate hyperparameters, such as a poorly chosen regularization parameter $C$ or kernel parameters, can lead to either overfitting or underfitting. Model evaluation helps determine whether the SVM is performing adequately on the given task, while hyperparameter tuning adjusts the model to achieve optimal performance.

The key hyperparameters that influence SVM performance are:

• Regularization parameter $C$: This controls the trade-off between maximizing the margin and minimizing classification errors. A high $C$ value tends to reduce the number of misclassified points but may result in a narrower margin, potentially leading to overfitting. Conversely, a low $C$ value allows for a wider margin but might tolerate more misclassifications, leading to underfitting.

• Kernel parameters: When using non-linear kernels, parameters such as $\gamma$ for the Radial Basis Function (RBF) kernel or the degree ddd for the polynomial kernel play a significant role. These parameters define the shape and complexity of the decision boundary, influencing the model's ability to capture intricate patterns in the data.

Hyperparameter tuning involves searching for the best combination of these parameters to optimize the SVM's performance on a given dataset.

Several evaluation metrics are available to assess the performance of SVM models, each providing different insights into the model's effectiveness. The most common metrics include:

• Accuracy: This metric measures the proportion of correctly classified instances out of the total number of instances. Although widely used, accuracy can be misleading in imbalanced datasets where one class dominates.

$$ \text{Accuracy} = \frac{\text{Number of Correct Predictions}}{\text{Total Number of Predictions}} $$

Precision: Precision quantifies the proportion of true positive predictions out of all positive predictions made by the model. It is particularly relevant in cases where false positives have a significant cost.

$$ \text{Precision} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Positives}} $$

Recall: Recall (or sensitivity) measures the proportion of true positives identified out of all actual positive instances. It is crucial in cases where missing positive instances is costly.

$$ \text{Recall} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Negatives}} $$

F1 Score: The F1 score is the harmonic mean of precision and recall, providing a balanced measure when there is an uneven class distribution.

$$ F1 = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} $$

ROC-AUC (Receiver Operating Characteristic - Area Under Curve): The ROC-AUC metric evaluates the model's ability to distinguish between classes by plotting the true positive rate against the false positive rate. A higher AUC indicates a better model performance in distinguishing between positive and negative classes.

For robust evaluation, cross-validation is employed. In k-fold cross-validation, the dataset is split into $k$ equal-sized subsets (folds). The model is trained on $k-1$ folds and evaluated on the remaining fold, and this process is repeated $k$ times with different folds used for validation each time. The average performance across all folds gives a more reliable estimate of the model's performance.

Hyperparameter tuning is typically conducted using techniques such as grid search and random search:

• Grid Search: This method involves specifying a set of possible values for each hyperparameter and systematically evaluating all combinations. Although exhaustive, grid search can be computationally expensive, especially when the parameter space is large.

• Random Search: Instead of evaluating all combinations, random search samples a fixed number of hyperparameter combinations from the parameter space. This method can be more efficient than grid search, particularly when certain hyperparameters have little influence on model performance.

Below is an example of implementing a pipeline in Rust using the linfa crate to perform model evaluation and hyperparameter tuning on an SVM model.

Example: SVM Model Evaluation and Hyperparameter Tuning with Linfa link

use linfa::prelude::*;
use linfa_svm::{Svm, SvmParams};
use ndarray::Array2;
use rand::seq::SliceRandom;
use std::collections::HashMap;

fn main() {
    // Define a simple dataset
    let data = Array2::from_shape_vec((10, 2), vec![
        1.0, 2.0, 2.0, 3.0, 3.0, 4.0, 4.0, 5.0, 5.0, 6.0,
        6.0, 7.0, 7.0, 8.0, 8.0, 9.0, 9.0, 10.0, 10.0, 11.0,
    ]).unwrap();
    let targets = Array2::from_shape_vec((10, 1), vec![
        1, 1, 1, 1, -1, -1, -1, -1, 1, 1,
    ]).unwrap();

    // Split dataset into training and test sets (80% train, 20% test)
    let mut dataset = Dataset::new(data, targets);
    let (train, test) = dataset.shuffle_split(0.8);

    // Define possible hyperparameter values for grid search
    let c_values = vec![0.1, 1.0, 10.0];
    let gamma_values = vec![0.1, 0.5, 1.0];
    let mut best_score = 0.0;
    let mut best_params = (0.0, 0.0);

    // Perform grid search
    for &c in &c_values {
        for &gamma in &gamma_values {
            // Create and train an SVM model with RBF kernel
            let model = SvmParams::new()
                .gaussian_kernel(gamma)
                .c(c)
                .fit(&train)
                .expect("Failed to train model");

            // Evaluate the model on the test set
            let predictions = model.predict(test.records());
            let accuracy = predictions.mean()
                .unwrap_or(0.0);

            println!("C: {}, Gamma: {}, Accuracy: {}", c, gamma, accuracy);

            // Track the best performing parameters
            if accuracy > best_score {
                best_score = accuracy;
                best_params = (c, gamma);
            }
        }
    }

    println!(
        "Best hyperparameters found - C: {}, Gamma: {}, with Accuracy: {}",
        best_params.0, best_params.1, best_score
    );
}

In this explanation, the dataset is created with input features and target labels, and the shuffle_split function is used to divide the data into training and test sets with an 80-20 split. A grid search is performed by iterating over predefined values of the hyperparameters $C$ and $\gamma$. For each combination, an SVM model is trained using the linfa library. The model is then evaluated on the test set by computing the accuracy for each combination of hyperparameters. The results help identify the best-performing hyperparameter values, which are then displayed along with their corresponding accuracy.

Model evaluation and hyperparameter tuning are critical steps in building an effective SVM model. By using metrics like accuracy, precision, recall, F1 score, and ROC-AUC, we can assess the model's performance comprehensively. Cross-validation provides a robust mechanism for estimating generalization performance, while techniques such as grid search and random search help identify optimal hyperparameters for the given task. Implementing these practices in Rust allows for efficient experimentation and tuning of SVM models, ensuring they perform well on complex datasets. This rigorous approach ensures that SVMs, whether used for classification or regression, are fine-tuned to capture the underlying patterns of the data effectively.

7.7. Conclusion link

Chapter 7 equips you with the knowledge and skills to implement and optimize Support Vector Machines for both classification and regression tasks using Rust. Mastering these techniques will enable you to build robust, high-performing models that can handle a wide range of machine learning challenges.

7.7.1. Further Learning with GenAI link

These prompts are designed to encourage deep exploration of the concepts and techniques related to Support Vector Machines (SVMs) and their implementation in Rust. Each prompt is intended to help you understand the underlying theory, apply it in Rust, and critically analyze the results.

• Explain the fundamental principles of Support Vector Machines. How do SVMs find the optimal hyperplane that separates different classes, and why is maximizing the margin important for generalization? Implement a basic SVM in Rust and apply it to a binary classification problem.

• Discuss the mathematical formulation of SVMs. How do convex optimization and the dual formulation contribute to solving the SVM problem? Implement the SVM optimization problem in Rust, focusing on the role of Lagrange multipliers and the Karush-Kuhn-Tucker (KKT) conditions.

• Analyze the concept of the kernel trick in SVMs. How does the kernel trick enable SVMs to handle non-linear data, and what are the most common types of kernels used? Implement kernelized SVMs in Rust, experimenting with different kernel functions on a non-linear dataset.

• Explore the differences between linear and non-linear SVMs. In what scenarios would you choose a non-linear SVM over a linear one, and how do kernel functions affect the decision boundary? Implement both linear and non-linear SVMs in Rust and compare their performance on a complex dataset.

• Discuss the concept of Support Vector Regression (SVR). How does SVR extend the SVM framework to handle regression tasks, and what is the role of the epsilon-insensitive loss function? Implement SVR in Rust and compare its performance with traditional regression methods on a real-world dataset.

• Analyze the trade-offs involved in using soft margin SVMs. How does the regularization parameter C affect the balance between margin size and classification error, and what are the implications for model performance? Implement soft margin SVMs in Rust and experiment with different values of C on a non-separable dataset.

• Explore the significance of the decision boundary in SVMs. How does the position of the decision boundary affect classification performance, and what factors influence its placement? Implement a visualization of the decision boundary in Rust for an SVM model applied to a binary classification problem.

• Discuss the role of support vectors in SVMs. Why are support vectors critical to defining the decision boundary, and how do they influence the SVM model? Implement a method in Rust to identify and visualize support vectors in an SVM model.

• Analyze the impact of different kernel functions on SVM performance. How do kernels like the radial basis function (RBF), polynomial, and sigmoid affect the decision boundary and model accuracy? Implement and compare these kernel functions in Rust on various datasets.

• Explore the use of cross-validation in evaluating SVM models. How does cross-validation help in assessing model generalization, and what are the best practices for implementing it? Implement cross-validation in Rust for an SVM model and analyze the results.

• Discuss the importance of hyperparameter tuning in SVMs. How do hyperparameters like C, kernel type, and gamma influence SVM performance, and what techniques can be used for tuning them? Implement a hyperparameter tuning pipeline in Rust using grid search or random search for an SVM model.

• Analyze the role of the slack variable in soft margin SVMs. How does the slack variable allow SVMs to handle misclassified points, and what is its relationship with the regularization parameter C? Implement a soft margin SVM in Rust and experiment with different slack variable settings.

• Explore the concept of duality in SVM optimization. How does the dual formulation of the SVM problem simplify the optimization process, and what are the advantages of solving the dual problem? Implement the dual formulation of SVM in Rust and compare it with the primal formulation.

• Discuss the limitations of SVMs and how they can be addressed. What challenges do SVMs face when dealing with large datasets, high-dimensional spaces, or noisy data, and how can these challenges be mitigated? Implement strategies in Rust to improve SVM performance in these scenarios.

• Analyze the application of SVMs to imbalanced datasets. How do SVMs handle class imbalance, and what techniques can be used to improve performance on imbalanced data? Implement an SVM in Rust for an imbalanced dataset and evaluate its performance using appropriate metrics.

• Explore the use of SVMs in multi-class classification. How can SVMs, which are inherently binary classifiers, be extended to handle multi-class problems, and what are the common approaches (e.g., one-vs-one, one-vs-all)? Implement a multi-class SVM in Rust and apply it to a dataset like the Iris dataset.

• Discuss the computational complexity of SVMs. How does the training time of SVMs scale with the number of training samples and the dimensionality of the feature space, and what techniques can be used to reduce computational cost? Implement an efficient SVM in Rust for a large dataset and analyze its scalability.

• Analyze the interpretability of SVM models. How can the coefficients and support vectors of an SVM be interpreted to gain insights into the model's decision-making process? Implement methods in Rust to interpret and visualize SVM model components.

• Explore the relationship between SVMs and other linear models, such as logistic regression. How do SVMs compare with logistic regression in terms of decision boundaries, loss functions, and performance on different types of data? Implement both SVM and logistic regression models in Rust and compare their results on the same dataset.

Each prompt offers an opportunity to explore, experiment, and refine your skills, helping you become a more proficient and knowledgeable machine learning practitioner. Embrace these challenges as a way to push the boundaries of your expertise and apply your knowledge to solve complex problems with SVMs and Rust.

7.7.2. Hands-On Practices link

These exercises are designed to be challenging and in-depth, requiring you to apply both theoretical knowledge and practical skills in Rust.