8.1. Introduction to Neural Network link

Neural networks are inspired by biological neural systems, where interconnected neurons transmit and process signals. In an artificial neural network (ANN), the basic computational unit is a neuron, which transforms an input vector $\mathbf{x} \in \mathbb{R}^d$ into an output through a weighted linear combination followed by a non-linear activation function. A neural network comprises multiple layers of such neurons, with the network’s depth and width dictating its capacity to learn intricate patterns.

At the core of a neural network is a neuron, or perceptron, which computes a weighted sum of its inputs and passes this sum through an activation function to produce an output. For a single neuron, this process can be written mathematically as:

$$ z = \mathbf{w}^T \mathbf{x} + b, $$

where $\mathbf{w} \in \mathbb{R}^d$ is the weight vector, $b \in \mathbb{R}$ is the bias term, $\mathbf{x} \in \mathbb{R}^d$ is the input vector, and $\sigma(z)$ is the activation function applied to the weighted sum $z$. The activation function introduces non-linearity into the network, enabling it to model non-linear relationships between input and output. Popular activation functions include:

• Sigmoid: $\sigma(z) = \frac{1}{1 + e^{-z}}$, which outputs values between 0 and 1.

• Hyperbolic tangent (tanh): $\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}$, which outputs values between -1 and 1.

• Rectified Linear Unit (ReLU): $\text{ReLU}(z) = \max(0, z)$, which outputs 0 for negative inputs and the input value for positive inputs.

A neural network consists of multiple layers: an input layer, one or more hidden layers, and an output layer. Each hidden layer receives the output from the previous layer, applies a linear transformation followed by a non-linear activation, and passes the result to the next layer. For a network with $L$ layers, the output $\mathbf{y}$ is computed as follows:

$$ \mathbf{y} = f(W_L \sigma(W_{L-1} \sigma(\cdots \sigma(W_1 \mathbf{x} + \mathbf{b}_1) + \mathbf{b}_{L-1}) + \mathbf{b}_L)), $$

where $W_i$ and $\mathbf{b}_i$ are the weight matrix and bias vector at layer $i$, $\sigma(\cdot)$ is the non-linear activation function, and $f(\cdot)$ is the output function, such as softmax for classification tasks. The network’s architecture, including the number of layers and the number of neurons per layer, determines its capacity to learn and represent different types of data.

The most basic form of a neural network is the feedforward neural network (FNN), where information flows in a single direction from the input layer to the output layer without cycles. The term "feedforward" refers to the lack of feedback loops in the network. FNNs are highly effective at modeling non-linear relationships between inputs and outputs, which is crucial in many real-world tasks such as image recognition, speech processing, and time series forecasting.

Mathematically, a feedforward neural network models a function $f(\mathbf{x})$ that maps an input $\mathbf{x}$ to an output $\mathbf{y}$ by composing a series of linear transformations and non-linear activations. The Universal Approximation Theorem states that a feedforward network with a single hidden layer and a sufficient number of neurons can approximate any continuous function to arbitrary accuracy on a compact subset of $\mathbb{R}^n$. This makes neural networks fundamentally powerful: by stacking layers and choosing appropriate activation functions, we can build models capable of approximating complex, non-linear functions.

To gain an intuitive understanding of how feedforward neural networks learn, interactive tools like the [TensorFlow Playground](https://playground.tensorflow.org/) are helpful. These tools allow users to visualize how different network architectures (i.e., the number of layers and neurons), activation functions, and regularization techniques influence the decision boundaries learned by the network. By experimenting with synthetic datasets, one can observe how deeper networks with more layers are better suited for modeling complex, non-linear relationships, while shallower networks may struggle to capture such complexity.

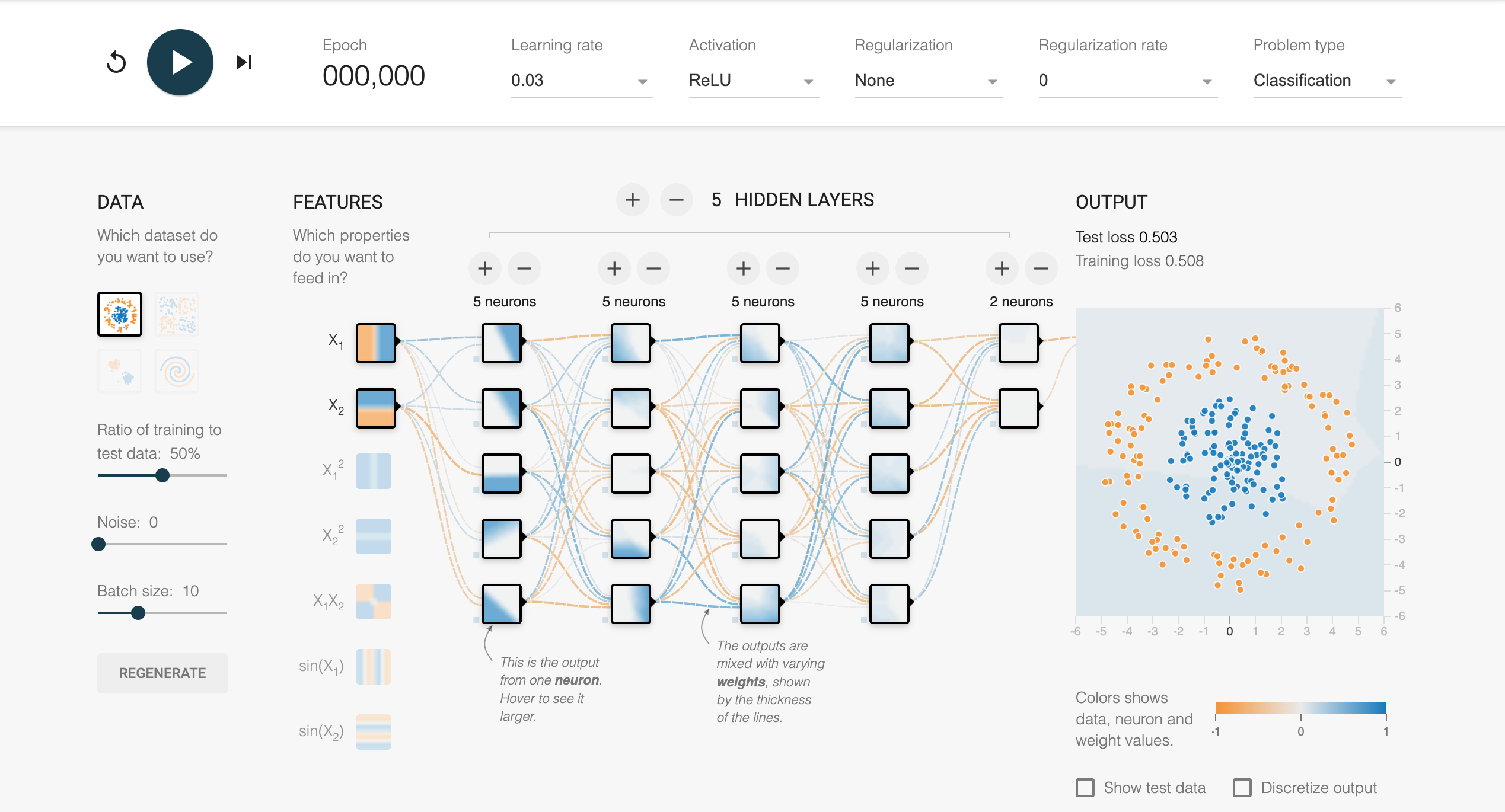
Figure 1: Tensorflow Playground to learn Neural Network visually.

Practically, implementing a simple feedforward neural network from scratch in Rust involves using libraries like tch-rs, which provides the necessary tools for tensor operations and automatic differentiation. The following steps outline a basic neural network implementation:

• Define the Network Architecture: A feedforward network consists of several layers, each defined by a weight matrix $W_i$ and a bias vector $\mathbf{b}_i$. In Rust, these layers can be represented using the nn::Linear module from the tch-rs crate.

• Initialize Parameters: The weights and biases are initialized randomly or using a specific initialization technique (e.g., Xavier initialization). These parameters will be updated during training using gradient-based optimization methods.

• Forward Pass: During the forward pass, the input is passed through each layer, where it undergoes a linear transformation followed by a non-linear activation. For classification tasks, the output layer typically uses a softmax function to convert the network’s output into class probabilities.

• Loss Function and Backpropagation: The loss function measures how well the network’s predictions match the true labels. For classification tasks, the cross-entropy loss is commonly used. Backpropagation computes the gradients of the loss with respect to the network’s parameters using automatic differentiation, which is crucial for updating the parameters to minimize the loss.

• Optimization: An optimizer like Stochastic Gradient Descent (SGD) or Adam is used to update the network’s parameters based on the gradients computed during backpropagation.

Here is an example of implementing a simple feedforward neural network in Rust using tch-rs:

use tch::{Tensor, nn, nn::Module, nn::OptimizerConfig};

struct FeedForwardNN {
    layers: Vec<nn::Linear>,
}

impl FeedForwardNN {
    fn new(vs: &nn::Path, input_size: i64, hidden_size: i64, output_size: i64) -> Self {
        let layer1 = nn::linear(vs, input_size, hidden_size, Default::default());
        let layer2 = nn::linear(vs, hidden_size, output_size, Default::default());
        FeedForwardNN { layers: vec![layer1, layer2] }
    }

    fn forward(&self, x: &Tensor) -> Tensor {
        let x = x.apply(&self.layers[0]).relu();
        x.apply(&self.layers[1]).softmax(-1, tch::Kind::Float)
    }
}

fn train_network() {
    let vs = nn::VarStore::new(tch::Device::Cpu);
    let net = FeedForwardNN::new(&vs.root(), 784, 128, 10);  // For MNIST dataset

    let mut opt = nn::Adam::default().build(&vs, 1e-3).unwrap();
    for epoch in 1..100 {
        let loss = net.forward(&train_data).cross_entropy_for_logits(&train_labels);
        opt.backward_step(&loss);
    }
}

In this example, the network consists of two layers: the first with 128 hidden neurons and ReLU activation, and the second with 10 output neurons for a classification task (e.g., the MNIST dataset). The training process involves iterating over the dataset, computing the loss using cross-entropy, and updating the weights using the Adam optimizer.

Neural networks are a powerful class of models capable of learning complex, non-linear mappings from data. By stacking layers of neurons and applying non-linear activation functions, neural networks can model intricate patterns that are otherwise difficult to capture using linear methods. Feedforward networks, while conceptually simple, provide the foundation for more advanced architectures like convolutional neural networks (CNNs) and recurrent neural networks (RNNs). Implementing neural networks in Rust using libraries like tch-rs enables developers to leverage Rust’s performance and safety guarantees while building efficient machine learning models.

8.2. Activation Functions and Their Roles link

Activation functions introduce the critical non-linearity that enables neural networks to model complex, non-linear relationships between inputs and outputs, transforming neural networks from simple linear classifiers into powerful models capable of learning highly intricate data representations. The mathematical properties of activation functions, their impact on training, and how to implement them efficiently in Rust using the tch-rs crate will be the focus.

Activation functions are the key components that govern how the input data is transformed as it propagates through a neural network. Without non-linear transformations, a neural network consisting of multiple layers would essentially collapse into a linear transformation, rendering it no more powerful than a single-layer perceptron. Several activation functions are commonly used in practice, each with distinct mathematical characteristics that define their behavior during training.

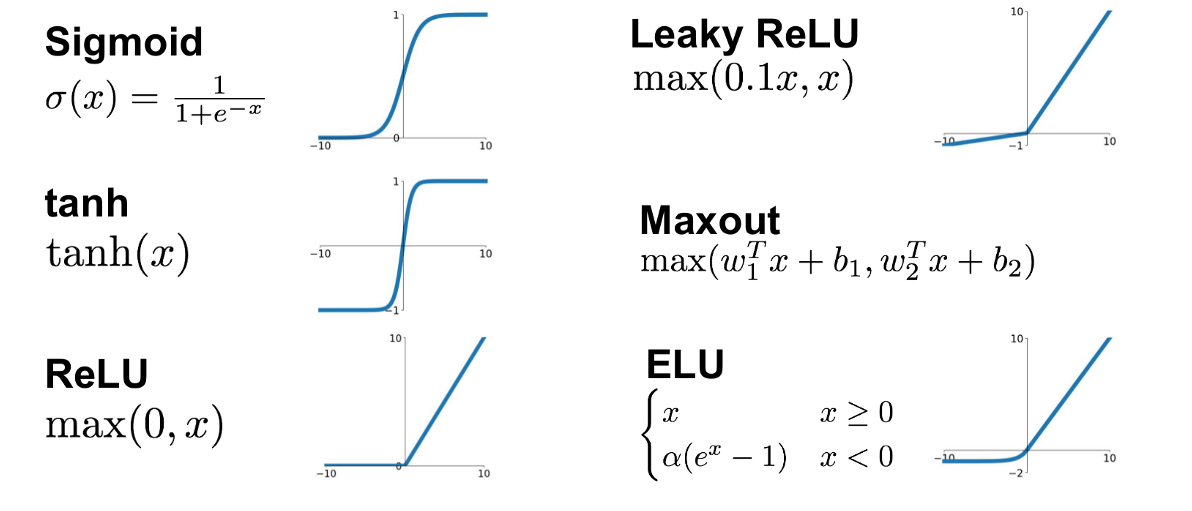
Figure 2: Activation functions for neural network.

The sigmoid activation function is defined as

$$\sigma(z) = \frac{1}{1 + e^{-z}},$$

where $z$ represents the input to the activation function. The sigmoid squashes the input values into a range between 0 and 1, making it ideal for binary classification tasks where the output needs to represent a probability. One key property of the sigmoid function is its smooth, continuous nature, which allows it to propagate small gradients during backpropagation. However, the derivative of the sigmoid function, $\sigma'(z) = \sigma(z)(1 - \sigma(z))$, becomes very small for large positive or negative values of $z$, leading to the vanishing gradient problem. This makes it difficult for deep neural networks to update weights effectively, particularly in layers far from the output layer.

The tanh function (hyperbolic tangent) is mathematically defined as:

$$\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}},$$

which maps input values to the range $[-1, 1]$. Like the sigmoid function, tanh is also smooth and differentiable, but it has a wider output range that is symmetric about zero. This property allows tanh to center data more effectively, which can be beneficial during training as it often leads to faster convergence compared to the sigmoid. The derivative of tanh is: $\tanh'(z) = 1 - \tanh^2(z)$, which, like sigmoid, suffers from the vanishing gradient problem when $z$ is very large or very small. Despite this, tanh is often preferred over sigmoid for hidden layers due to its better centering properties.

The Rectified Linear Unit (ReLU) activation function is defined as:

$$\text{ReLU}(z) = \max(0, z). $$

ReLU is a piecewise linear function that outputs $z$ for positive inputs and 0 for negative inputs. This simplicity results in highly efficient computation and, more importantly, helps mitigate the vanishing gradient problem by maintaining a constant gradient of 1 for positive inputs. This allows ReLU to propagate meaningful gradients through deep networks, making it the most widely used activation function in modern deep learning architectures. However, ReLU suffers from the dying ReLU problem, where neurons may become inactive if they receive negative inputs consistently, leading them to output zero and stop updating during training. The derivative of ReLU is:

$$\text{ReLU}'(z) = \begin{cases} 1 & \text{if } z > 0, \\ 0 & \text{if } z \leq 0. \end{cases}$$

This property explains why ReLU is computationally efficient and works well for deep networks but also highlights the problem when large portions of the input space produce zero gradients.

To address the dying ReLU problem, Leaky ReLU introduces a small, non-zero slope for negative inputs:

$$\text{Leaky ReLU}(z) = \max(0.01z, z),$$

where 0.01 is the default slope for negative values. This ensures that even negative inputs propagate a small gradient, thus allowing neurons to continue updating. An extension of this idea, Parametric ReLU (PReLU), allows the slope to be a learned parameter during training: $\text{PReLU}(z) = \max(\alpha z, z),$ where $\alpha$ is a learned parameter. This added flexibility enables the network to adjust the activation function’s behavior based on the data, potentially improving performance.

The core conceptual idea behind activation functions is the introduction of non-linearity into neural networks. If a neural network used only linear transformations between layers, it would be unable to model complex, non-linear relationships, regardless of the number of layers. Activation functions solve this problem by applying non-linear transformations at each layer, enabling the network to approximate highly complex functions.

The Universal Approximation Theorem asserts that a feedforward neural network with a single hidden layer and a non-linear activation function can approximate any continuous function to an arbitrary degree of accuracy, given sufficient neurons. This is a powerful theoretical result that underpins the use of neural networks for a wide range of tasks. However, the practical performance of a neural network depends heavily on the choice of activation function, which influences gradient flow, convergence speed, and the network’s ability to generalize.

For instance, sigmoid and tanh functions were historically popular in neural network architectures, but they suffer from the vanishing gradient problem, which impedes the training of deep networks. In contrast, ReLU avoids this problem by providing large gradients for positive inputs, which accelerates training, especially in deeper networks. However, ReLU’s sparse activations—where neurons are deactivated for a significant portion of the input space—can sometimes be beneficial by introducing regularization effects that prevent overfitting, but in other cases, it may lead to under-utilization of neurons.

In practice, the depth of the network and the nature of the data will guide the choice of activation function. For example, deep convolutional networks often use ReLU in hidden layers due to its efficiency and strong gradient propagation, while networks dealing with sequential data or tasks requiring smooth output distributions may use sigmoid or tanh functions.

To gain a deeper understanding of the impact of activation functions, it is essential to implement and experiment with them in a practical context. Using the tch-rs crate, we can efficiently implement various activation functions and apply them to different neural network architectures. The following Rust code demonstrates how to implement common activation functions using tch-rs:

use tch::{Tensor, Kind};

// Sigmoid Activation Function
fn sigmoid(x: &Tensor) -> Tensor {
    x.sigmoid()
}

// Tanh Activation Function
fn tanh(x: &Tensor) -> Tensor {
    x.tanh()
}

// ReLU Activation Function
fn relu(x: &Tensor) -> Tensor {
    x.relu()
}

// Leaky ReLU Activation Function
fn leaky_relu(x: &Tensor) -> Tensor {
    x.maximum(&(x * 0.01))
}

// Parametric ReLU (PReLU) Activation Function
fn prelu(x: &Tensor, alpha: &Tensor) -> Tensor {
    Tensor::maximum(&(alpha * x), x)
}

fn main() {
    // Sample input tensor
    let input = Tensor::from_slice(&[0.5, -0.5, 0.1, -0.1]).to_kind(Kind::Float);
    
    // Applying different activation functions
    let sigmoid_output = sigmoid(&input);
    let tanh_output = tanh(&input);
    let relu_output = relu(&input);
    let leaky_relu_output = leaky_relu(&input);
    let alpha = Tensor::from_slice(&[0.01]).to_kind(Kind::Float);
    let prelu_output = prelu(&input, &alpha);
    
    println!("Sigmoid Output: {:?}", sigmoid_output);
    println!("Tanh Output: {:?}", tanh_output);
    println!("ReLU Output: {:?}", relu_output);
    println!("Leaky ReLU Output: {:?}", leaky_relu_output);
    println!("PReLU Output: {:?}", prelu_output);
}

In this implementation, we define functions for the sigmoid, tanh, ReLU, Leaky ReLU, and Parametric ReLU activation functions and apply them to a sample input tensor. By experimenting with different activation functions and observing their effects on network training, we can evaluate which functions perform best under various conditions. This can be done by training a simple feedforward neural network on a dataset (e.g., MNIST) and comparing the results based on accuracy, training loss, convergence rate, and generalization performance.

To gain deeper intuition, tools like Deeper Playground allow users to visualize how different activation functions affect learning. Through interactive experimentation, users can explore the behavior of different activation functions on synthetic datasets. For instance, ReLU tends to produce sharp, piecewise-linear decision boundaries, while sigmoid and tanh often result in smoother boundaries. By observing how activation functions change the learning dynamics, one can better understand which activation functions are appropriate for specific tasks and architectures.

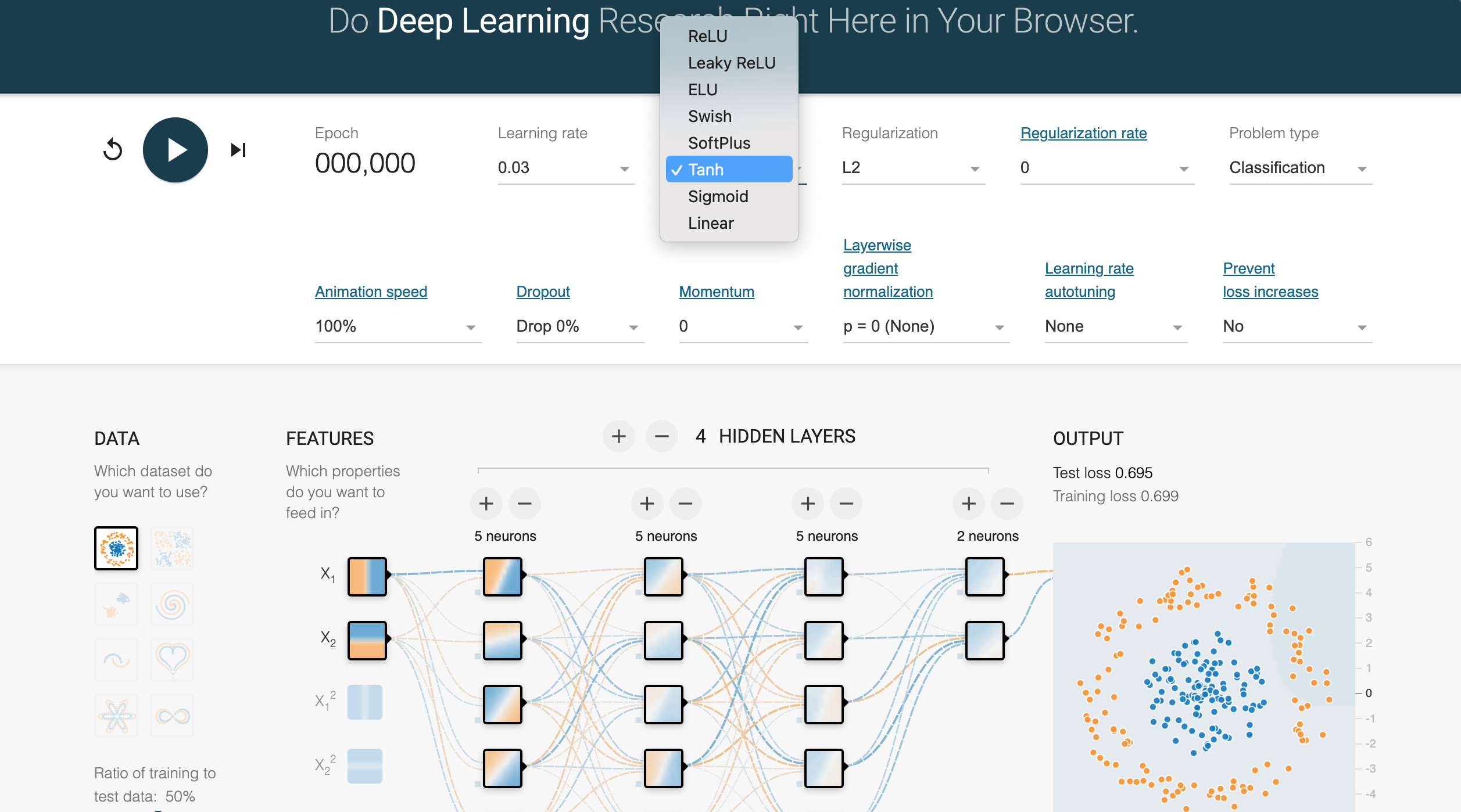
Figure 3: Deeper Playground visual tools for Neural Network.

The choice of activation function is critical for the effective training of neural networks, particularly for deep architectures. Sigmoid and tanh are smooth, continuous functions that were historically popular but are prone to the vanishing gradient problem in deep networks. ReLU, with its simplicity and gradient-preserving properties, has become the default choice in many modern architectures. Variants like Leaky ReLU and Parametric ReLU offer solutions to ReLU’s limitations, such as the dying ReLU problem, by ensuring that gradients continue to propagate for negative inputs.

In practice, selecting the best activation function requires understanding the nature of the problem, the architecture of the network, and the impact on gradient flow during training. Experimenting with different activation functions, as demonstrated in Rust using the tch-rs crate, is essential for optimizing neural network performance.

8.3. Backpropagation and Gradient Descent link

Backpropagation and gradient descent form the backbone of neural network training. The process of adjusting the weights and biases in a neural network to minimize error is achieved through an efficient combination of calculus, matrix operations, and optimization techniques. This section delves into the intricate mathematical details of these algorithms, exploring how the gradients are computed via backpropagation and how gradient descent uses these gradients to optimize the network’s performance. We will also cover practical aspects, such as implementing these methods in Rust, experimenting with different loss functions, and exploring the effects of hyperparameters like learning rates on model convergence.

Backpropagation is a method for efficiently computing the gradients of the loss function with respect to each parameter (weights and biases) in the network. A neural network can be viewed as a function composed of multiple sub-functions (layers). Each of these layers performs a linear transformation followed by a non-linear activation function. When training the network, the goal is to minimize the loss function, which measures how well the network's predictions align with the true labels. Backpropagation computes the gradients of this loss function with respect to the network's parameters using the chain rule of calculus, which allows us to decompose the derivative of a composite function into a product of simpler derivatives.

Consider a feedforward neural network with $L$ layers. For an input vector $\mathbf{x}$, the output of the network is denoted as:

$$ \mathbf{y} = f(\mathbf{x}; \theta), $$

where $\theta$ represents the set of all parameters (weights and biases) of the network. Let $\mathcal{L}(\mathbf{y}, \mathbf{t})$ be the loss function, where $\mathbf{t}$ is the true label. The goal is to minimize this loss function with respect to the parameters $\theta$.

For each layer $l$, we have the following operations:

$$ \mathbf{z}_l = W_l \mathbf{a}_{l-1} + \mathbf{b}_l, $$

$$ \mathbf{a}_l = \sigma(\mathbf{z}_l), $$

where $\mathbf{a}_{l-1}$ is the activation from the previous layer, $W_l$ is the weight matrix, $\mathbf{b}_l$ is the bias vector, and $\sigma$ is the activation function (e.g., ReLU, sigmoid). The network output $\mathbf{y}$ is compared to the true label $\mathbf{t}$ using a loss function $\mathcal{L}$, such as mean squared error (MSE) or cross-entropy.

The task is to compute the partial derivatives of the loss with respect to the weights and biases at each layer, $\frac{\partial \mathcal{L}}{\partial W_l}$ and $\frac{\partial \mathcal{L}}{\partial \mathbf{b}_l}$, and then update these parameters using gradient descent.

Gradient Descent is an iterative optimization algorithm that updates the parameters of the network in the direction that minimizes the loss function. The update rule for gradient descent is given by:

$$ \theta \leftarrow \theta - \eta \nabla_{\theta} \mathcal{L}, $$

where $\eta$ is the learning rate, a hyperparameter that controls the size of the update step, and $\nabla_{\theta} \mathcal{L}$ is the gradient of the loss with respect to the parameters $\theta$. The learning rate is crucial for balancing the convergence speed and stability. A learning rate that is too large may cause the algorithm to overshoot the optimal solution, while a learning rate that is too small may lead to slow convergence.

The backpropagation algorithm heavily relies on the chain rule of calculus. The chain rule states that if a function is composed of several nested functions, the derivative of the overall function can be expressed as the product of the derivatives of the individual functions. This is crucial in neural networks because the final output is the result of applying a series of transformations at each layer, and backpropagation requires us to compute how the loss function changes as a function of the parameters in each layer.

For each layer $l$, we define the error signal $\delta_l$, which represents the gradient of the loss with respect to the input $\mathbf{z}_l$ of layer $l$. By applying the chain rule, we can express $\delta_l$ recursively:

$$ \delta_l = (\delta_{l+1} W_{l+1}) \circ \sigma'(\mathbf{z}_l), $$

where $\circ$ represents element-wise multiplication, and $\sigma'(\mathbf{z}_l)$ is the derivative of the activation function with respect to $\mathbf{z}_l$. This recursive relation allows us to propagate the error signal backward through the network, layer by layer, starting from the output layer and moving toward the input layer. Once the error signal for each layer is computed, the gradients of the loss with respect to the weights and biases can be computed as:

$$ \frac{\partial \mathcal{L}}{\partial W_l} = \delta_l \mathbf{a}_{l-1}^T, $$

$$ \frac{\partial \mathcal{L}}{\partial \mathbf{b}_l} = \delta_l. $$

These gradients are then used in the gradient descent update step to adjust the parameters of the network.

The loss function plays a key role in backpropagation, as it defines the objective that the network is trying to optimize. The choice of the loss function depends on the type of problem being solved (e.g., classification, regression) and has a significant impact on the gradient flow during training.

For regression tasks, the most commonly used loss function is the mean squared error (MSE), defined as:

$$ \mathcal{L}_{MSE}(\mathbf{y}, \mathbf{t}) = \frac{1}{n} \sum_{i=1}^{n} (\mathbf{y}_i - \mathbf{t}_i)^2, $$

where $n$ is the number of training samples, $\mathbf{y}_i$ is the predicted value for the $i$-th sample, and $\mathbf{t}_i$ is the true value. The MSE loss penalizes large deviations between the predicted and true values, and its derivative with respect to the output is:

$$ \frac{\partial \mathcal{L}_{MSE}}{\partial \mathbf{y}_i} = 2 (\mathbf{y}_i - \mathbf{t}_i).∂yi​ $$

For classification tasks, the cross-entropy loss is typically used:

$$ \mathcal{L}_{CE}(\mathbf{y}, \mathbf{t}) = - \sum_{i=1}^{n} \mathbf{t}_i \log(\mathbf{y}_i), $$

where $\mathbf{y}_i$ represents the predicted probability for the $i$-th class, and $\mathbf{t}_i$ is the true class label. The cross-entropy loss measures the dissimilarity between the predicted and true distributions, and its derivative is:

$$ \frac{\partial \mathcal{L}_{CE}}{\partial \mathbf{y}_i} = - \frac{\mathbf{t}_i}{\mathbf{y}_i}.∂yi​ $$

The gradients of these loss functions are propagated through the network via backpropagation, enabling the network to adjust its parameters to reduce the overall error.

Implementing backpropagation and gradient descent in Rust can be done using the tch-rs crate, which provides tensor operations, automatic differentiation, and optimization tools. Below, we implement a simple feedforward neural network that uses backpropagation and gradient descent to minimize the MSE loss on a regression task.

use tch::{nn, nn::OptimizerConfig, Tensor};

struct NeuralNetwork {
    fc1: nn::Linear,
    fc2: nn::Linear,
}

impl NeuralNetwork {
    fn new(vs: &nn::Path, input_size: i64, hidden_size: i64, output_size: i64) -> Self {
        let fc1 = nn::linear(vs, input_size, hidden_size, Default::default());
        let fc2 = nn::linear(vs, hidden_size, output_size, Default::default());
        NeuralNetwork { fc1, fc2 }
    }

    fn forward(&self, x: &Tensor) -> Tensor {
        x.apply(&self.fc1).relu().apply(&self.fc2)
    }

    fn train(&self, vs: &nn::VarStore, data: &Tensor, target: &Tensor, learning_rate: f64, epochs: i64) {
        let mut opt = nn::Adam::default().build(vs, learning_rate).unwrap();
        for epoch in 0..epochs {
            let output = self.forward(&data);
            let loss = output.mse_loss(target, tch::Reduction::Mean);
            opt.backward_step(&loss);
            println!("Epoch: {}, Loss: {}", epoch, loss.to_dtype(tch::Kind::Float, true, true));
        }
    }
}

fn main() {
    let vs = nn::VarStore::new(tch::Device::Cpu);
    let network = NeuralNetwork::new(&vs.root(), 1, 128, 1);

    // Generate synthetic training data
    let x_train = Tensor::randn(&[100, 1], tch::kind::FLOAT_CPU);
    let y_train = 3.0 * &x_train + 2.0 + Tensor::randn(&[100, 1], tch::kind::FLOAT_CPU) * 0.1;

    // Train the network using backpropagation and gradient descent
    network.train(&vs, &x_train, &y_train, 0.01, 1000);
}

In this implementation, we define a simple two-layer neural network. The train method applies backpropagation by computing the mean squared error (MSE) loss and updating the network’s parameters using the Adam optimizer. The Adam optimizer is a variant of gradient descent that combines momentum and adaptive learning rates to improve convergence.

To experiment with different loss functions, we can replace the MSE loss with a cross-entropy loss when dealing with classification tasks. Furthermore, varying the learning rate during training allows us to observe how it affects the convergence behavior. A larger learning rate may result in faster convergence but risks overshooting the optimal solution, while a smaller learning rate may ensure more stable convergence but at the cost of slower training.

In conclusion, backpropagation and gradient descent are essential for training neural networks. By applying the chain rule, backpropagation efficiently computes the gradients of the loss function with respect to each parameter, and gradient descent uses these gradients to iteratively update the network’s parameters. By implementing these algorithms in Rust, we can experiment with different architectures, loss functions, and hyperparameters to optimize the performance of neural networks.

8.4. Regularization and Normalization link

In deep learning, regularization and normalization are pivotal techniques for enhancing the performance, generalization, and training stability of neural networks. Without these techniques, deep neural networks are highly prone to overfitting and inefficient convergence, leading to suboptimal model performance. Regularization methods are designed to control the complexity of the model by adding constraints on the weights, preventing the network from overfitting to the training data. Normalization methods, on the other hand, standardize the inputs to different layers to accelerate training and improve convergence by maintaining stable activations across layers.

Regularization techniques penalize the complexity of a neural network, discouraging it from fitting the noise in the training data and improving its generalization ability. The two most widely used regularization techniques are L2 regularization (also called weight decay) and dropout.

L2 regularization is one of the most commonly used regularization techniques. It works by adding a penalty term to the loss function, proportional to the squared magnitude of the weights in the network. Let’s start by defining the loss function $\mathcal{L}(\mathbf{y}, \mathbf{t})$ is the predicted output and $\mathbf{t}$ is the true label. In the case of regression, this loss function could be the mean squared error:

$$ \mathcal{L}(\mathbf{y}, \mathbf{t}) = \frac{1}{n} \sum_{i=1}^{n} (\mathbf{y}_i - \mathbf{t}_i)^2. $$

With L2 regularization, the loss function is augmented by an additional term, penalizing the sum of the squared values of the model’s weights:

$$ \mathcal{L}_{\text{reg}} = \mathcal{L}(\mathbf{y}, \mathbf{t}) + \frac{\lambda}{2} \sum_{l=1}^{L} \| W_l \|_2^2, $$

where $W_l$ is the weight matrix of layer $l$, $\lambda$ is a hyperparameter controlling the regularization strength, and $L$ is the number of layers in the network. The L2 regularization term $\frac{\lambda}{2} \sum_{l=1}^{L} \| W_l \|_2^2$ penalizes large weight values, which forces the network to distribute weight more evenly across features and discourages the model from relying heavily on a small subset of features. This approach reduces variance, thereby improving the model’s ability to generalize.

From an optimization perspective, L2 regularization modifies the gradient of the loss with respect to the weights during backpropagation. The gradient of the regularized loss with respect to the weights $W_l$ is:

$$ \frac{\partial \mathcal{L}_{\text{reg}}}{\partial W_l} = \frac{\partial \mathcal{L}}{\partial W_l} + \lambda W_l.∂Wl​ $$

This additional term $\lambda W_l$ effectively reduces the magnitude of the weights over time, leading to a form of weight decay that limits the model’s capacity to overfit.

Dropout is a more modern regularization technique that works by randomly "dropping out" a fraction of the neurons during each forward pass in the training phase. By dropping out neurons, the network is forced to learn redundant representations, as no single neuron can rely too heavily on other specific neurons to make predictions.

Mathematically, let $\mathbf{a}_l$ be the activation of layer $l$ in the network. Dropout modifies the activations by applying a random binary mask $\mathbf{m}_l$ drawn from a Bernoulli distribution with parameter $p$ (where $p$ is the probability of keeping a neuron active):

$$ \tilde{\mathbf{a}}_l = \mathbf{m}_l \circ \mathbf{a}_l, $$

where $\circ$ denotes element-wise multiplication. During each training iteration, a different set of neurons is dropped, encouraging the network to develop more robust feature detectors that do not rely on any specific neuron.

During inference (i.e., testing), dropout is no longer applied. Instead, the activations are scaled by the probability ppp to account for the dropped neurons during training:

$$ \tilde{\mathbf{a}}_l^{\text{test}} = p \cdot \mathbf{a}_l. $$

This scaling ensures that the expected output remains consistent between training and inference. Dropout is particularly effective in preventing overfitting, especially in large networks.

While regularization focuses on preventing overfitting, normalization techniques aim to accelerate training and stabilize convergence. Normalization methods such as batch normalization help reduce internal covariate shift, where the distribution of the inputs to each layer changes during training due to updates in the parameters of previous layers. This shift can make training deep networks challenging, as the network must constantly adapt to changing input distributions. By normalizing the inputs to each layer, normalization methods improve the training dynamics and allow the use of higher learning rates.

Batch normalization (BN) is the most common normalization technique used in deep neural networks. It standardizes the inputs to each layer so that they have zero mean and unit variance across the mini-batch, helping to maintain stable activations. Given a mini-batch of activations $\mathbf{a}_l$ at layer $l$, batch normalization computes the mean $\mu_l$ and variance $\sigma_l^2$ of the activations across the mini-batch:

$$ \mu_l = \frac{1}{m} \sum_{i=1}^{m} a_{l,i}, \quad \sigma_l^2 = \frac{1}{m} \sum_{i=1}^{m} (a_{l,i} - \mu_l)^2, $$

where $m$ is the number of examples in the mini-batch, and $ia_{l,i}$ is the activation for the iii-th example in layer $l$. The activations are then normalized as follows:

$$ \hat{\mathbf{a}}_l = \frac{\mathbf{a}_l - \mu_l}{\sqrt{\sigma_l^2 + \epsilon}}, $$

where $\epsilon$ is a small constant added for numerical stability. After normalization, the activations are scaled and shifted using learned parameters $\gamma_l$ and $\beta_l$:

$$ \tilde{\mathbf{a}}_l = \gamma_l \hat{\mathbf{a}}_l + \beta_l. $$

Batch normalization improves the flow of gradients through the network, reduces the sensitivity to weight initialization, and allows for the use of higher learning rates, speeding up training. Furthermore, by reducing the dependency on careful initialization and other hyperparameters, batch normalization helps networks converge faster and more reliably.

Overfitting is a primary concern in machine learning, particularly in large models with many parameters. Regularization techniques address this issue by constraining the capacity of the model, effectively penalizing complexity and encouraging the network to generalize better to unseen data. L2 regularization ensures that the network assigns smaller weights to less important features, while dropout forces the network to learn robust representations by preventing co-adaptation between neurons.

On the other hand, normalization techniques like batch normalization primarily aim to stabilize and accelerate the training process. By normalizing the inputs to each layer, batch normalization reduces internal covariate shifts, ensuring that each layer receives inputs with a stable distribution throughout training. This stabilization improves gradient flow, which in turn leads to faster convergence and more efficient use of the learning rate.

These techniques complement each other: regularization improves the generalization capability of the model, while normalization speeds up convergence and makes the training process more stable and efficient. Using both methods together is common in practice, especially in deep learning architectures such as convolutional neural networks (CNNs) and recurrent neural networks (RNNs).

To implement these techniques in Rust, we will use the tch-rs crate, which provides tensor operations and the ability to define neural network layers. Below is an implementation that combines L2 regularization, dropout, and batch normalization in a feedforward neural network.

use tch::{nn::{self, ModuleT, OptimizerConfig}, Tensor};

struct NeuralNetwork {
    fc1: nn::Linear,
    bn1: nn::BatchNorm,
    fc2: nn::Linear,
    dropout: f64,
}

impl NeuralNetwork {
    fn new(vs: &nn::Path, input_size: i64, hidden_size: i64, output_size: i64, dropout: f64) -> Self {
        let fc1 = nn::linear(vs, input_size, hidden_size, Default::default());
        let bn1 = nn::batch_norm1d(vs, hidden_size, Default::default());
        let fc2 = nn::linear(vs, hidden_size, output_size, Default::default());
        NeuralNetwork { fc1, bn1, fc2, dropout }
    }

    fn forward(&self, x: &Tensor, train: bool) -> Tensor {
        let mut x = x.apply(&self.fc1).relu();
        x = self.bn1.forward_t(&x, train);
        let x = if train { x.dropout(self.dropout, train) } else { x };
        x.apply(&self.fc2)
    }

    fn train_network(&self, vs: &nn::VarStore, data: &Tensor, target: &Tensor, learning_rate: f64, epochs: i64) {
        let mut opt = nn::Adam::default().build(vs, learning_rate).unwrap();
        for epoch in 0..epochs {
            let output = self.forward(&data, true);
            let loss = output.mse_loss(target, tch::Reduction::Mean) + self.l2_penalty(0.001);  // Adding L2 regularization
            opt.backward_step(&loss);
            println!("Epoch: {}, Loss: {}", epoch, loss.to_dtype(tch::Kind::Float, true, true));
        }
    }

    fn l2_penalty(&self, lambda: f64) -> Tensor {
        let weights = vec![&self.fc1.ws, &self.fc2.ws];
        let mut penalty = Tensor::zeros(&[], tch::kind::FLOAT_CPU);
        for w in weights {
            penalty += w.pow_tensor_scalar(2).sum(tch::kind::FLOAT_CPU.0);
        }
        penalty * lambda / 2.0
    }
}

fn main() {
    let vs = nn::VarStore::new(tch::Device::Cpu);
    let network = NeuralNetwork::new(&vs.root(), 1, 128, 1, 0.5);

    // Generate synthetic training data
    let x_train = Tensor::randn(&[100, 1], tch::kind::FLOAT_CPU);
    let y_train = 3.0 * &x_train + 2.0 + Tensor::randn(&[100, 1], tch::kind::FLOAT_CPU) * 0.1;

    network.train_network(&vs, &x_train, &y_train, 0.01, 1000);
}

In deep learning, regularization and normalization are indispensable tools for optimizing neural networks. Regularization techniques like L2 regularization and dropout mitigate overfitting by constraining the network’s capacity to learn overly complex or spurious relationships in the data. L2 regularization achieves this by penalizing large weights, while dropout promotes robust learning by randomly deactivating neurons during training.

Meanwhile, normalization techniques, especially batch normalization, improve training stability and efficiency by normalizing the inputs to each layer, reducing internal covariate shift, and allowing the use of higher learning rates. By incorporating these techniques into neural network architectures, we can achieve better generalization and faster, more stable training.

8.5. Deep Neural Networks and Convolutional Networks link

Deep neural networks (DNNs) and convolutional neural networks (CNNs) have fundamentally transformed the landscape of machine learning, enabling breakthroughs in tasks like image recognition, speech processing, and natural language understanding. These architectures leverage the depth and hierarchy of layers to extract increasingly complex features from data, making them well-suited for tasks with high-dimensional inputs.

A deep neural network (DNN) consists of multiple hidden layers stacked between the input and output layers. This depth is crucial for learning hierarchical representations from raw data. Each layer in the network performs a linear transformation followed by a non-linear activation, allowing the network to model complex, non-linear functions.

Mathematically, the forward pass through a DNN with $L$ layers can be represented as follows. Given an input vector $\mathbf{x} \in \mathbb{R}^d$, the output $\mathbf{y}$ is computed by sequentially applying linear transformations and non-linear activation functions across layers:

$$ \mathbf{z}_1 = W_1 \mathbf{x} + \mathbf{b}_1, \quad \mathbf{a}_1 = \sigma(\mathbf{z}_1), $$

$$ \mathbf{z}_2 = W_2 \mathbf{a}_1 + \mathbf{b}_2, \quad \mathbf{a}_2 = \sigma(\mathbf{z}_2), $$

$$\vdots$$

$$ \mathbf{z}_L = W_L \mathbf{a}_{L-1} + \mathbf{b}_L, \quad \mathbf{y} = f(\mathbf{z}_L). $$

Here, $W_i \in \mathbb{R}^{n_i \times n_{i-1}}$ represents the weight matrix for layer $i$, $\mathbf{b}_i \in \mathbb{R}^{n_i}$ is the bias term, and $\sigma(\cdot)$ is a non-linear activation function like ReLU or sigmoid. The function $f(\cdot)$ is often a softmax in classification tasks, mapping the network’s final layer output to probabilities.

The depth of a network allows it to capture increasingly abstract features as the data moves from layer to layer. For example, in image classification, shallow layers might detect edges, textures, or simple shapes, while deeper layers can identify object parts or even whole objects. However, increasing depth introduces challenges like the vanishing gradient problem, where gradients become very small as they propagate back through many layers during training, slowing down or even preventing learning in early layers.

Convolutional neural networks (CNNs) are a special class of neural networks designed to process data with a grid-like structure, such as images. CNNs are built upon the idea of convolutional layers, which apply filters to local regions of the input to extract spatial features. These filters, or kernels, are small matrices that slide over the input image and compute dot products at each spatial location, forming feature maps.

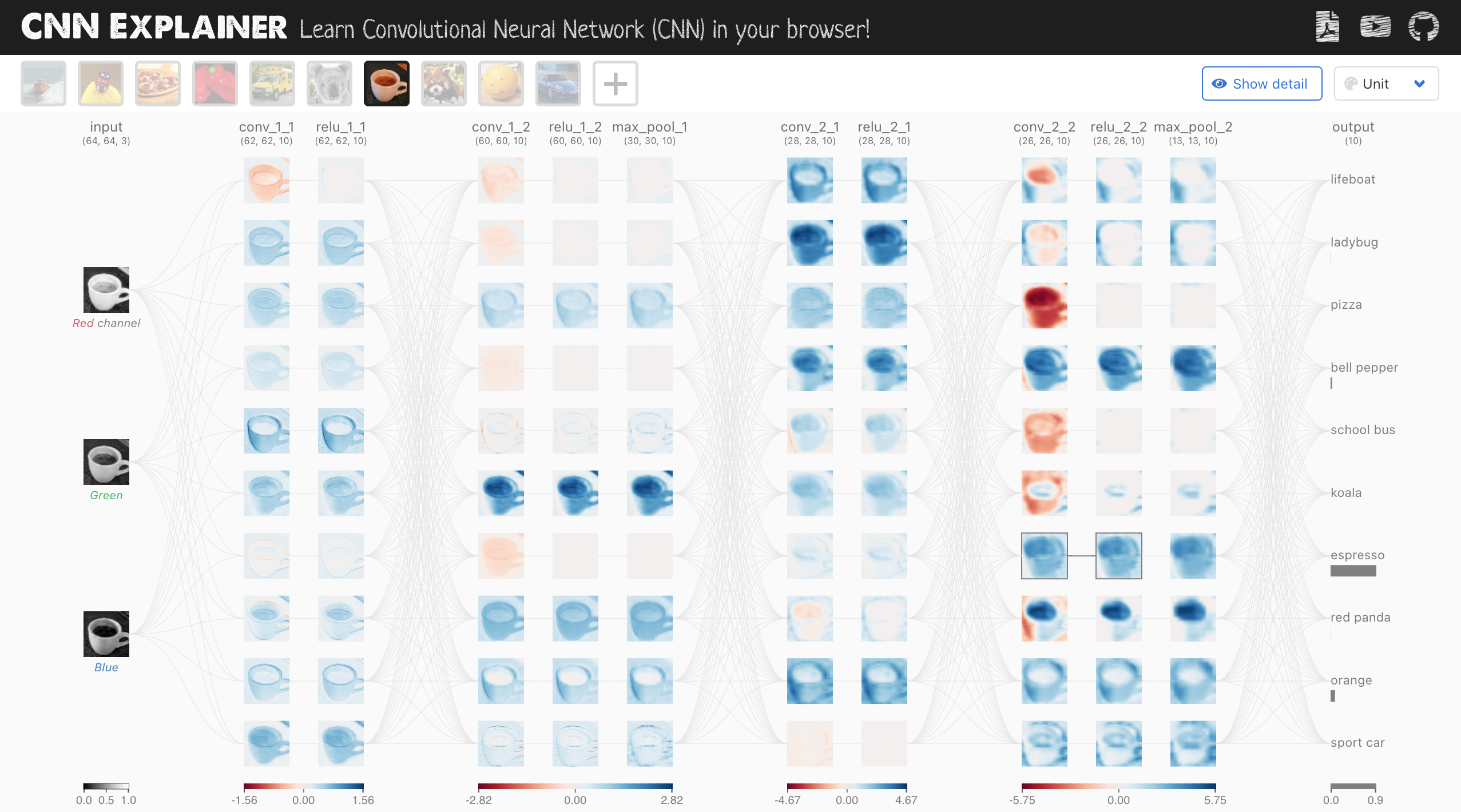
Figure 4: Learn how CNN works using CNN explainer.

The input to a CNN is typically a multi-dimensional array, or tensor, which in the case of an image could have three dimensions: height, width, and depth (the number of channels such as red, green, and blue in an RGB image). Each neuron in a CNN applies a learned kernel (or some time called filter) to a local region of the input to extract spatial features. These kernels are the weights that are learned during the training process, allowing the CNN to adapt to the data and the problem at hand. The process of applying a kernel to an input tensor results in a transformed output tensor, often visualized as activation maps in the network. Each layer in the CNN can have multiple kernels, with each kernel responsible for identifying different features in the image, such as edges, textures, or more complex patterns as you move deeper into the network.

CNNs differ from traditional fully connected neural networks due to their ability to preserve spatial structure in the data. This is achieved by having each neuron in a convolutional layer connected only to a local region of the input (rather than all inputs as in fully connected layers). This local connectivity allows CNNs to detect spatial hierarchies of features, which is crucial for tasks like image classification. The convolution operation is the core of this process, where a kernel slides across the input tensor and computes a dot product at each position. The output of this operation is a feature map that captures local information about the input. In practice, convolutional layers can be stacked, with the output of one layer serving as the input to the next. As the network deepens, each subsequent layer detects increasingly abstract and complex features, eventually leading to the classification of the input image.

An important hyperparameter in the design of convolutional layers is the kernel size, which determines the size of the local region over which the convolution is applied. A smaller kernel size allows the network to capture fine-grained details and enables the construction of deeper networks, as the spatial dimensions of the feature maps reduce more gradually. Conversely, larger kernels capture broader patterns but result in faster spatial reduction, often making it harder to build deeper networks without losing important spatial information. Another critical hyperparameter is the stride, which defines how far the kernel moves during each step of the convolution. A stride of 1 means the kernel shifts one pixel at a time, while larger strides skip over pixels, resulting in smaller output feature maps. The choice of stride affects both the resolution of the learned features and the computational complexity of the network.

The padding technique is often employed to preserve the spatial dimensions of the input, especially when using smaller kernel sizes. Padding involves adding extra pixels (usually zeros) around the border of the input tensor, ensuring that the kernel can slide over the entire image, including the edges. This allows the network to build deeper architectures without excessively reducing the size of the feature maps at each layer. Common padding strategies include zero-padding, which is computationally efficient and easy to implement, making it a standard choice in many high-performing CNN architectures such as AlexNet, ResNet and DenseNet.

Activation functions like ReLU (Rectified Linear Unit) are applied after each convolutional layer to introduce non-linearity into the model. This non-linearity is essential for CNNs to learn complex patterns and decision boundaries that go beyond linear relationships between input and output. The ReLU function outputs the input directly if it is positive, and zero otherwise. This simple, yet powerful, non-linear transformation ensures that the network can model non-linear relationships and is a key reason for the success of modern CNNs. Without non-linear activation functions, the CNN would behave like a linear model, incapable of capturing the rich patterns in the data. ReLU is preferred over other non-linear functions like the sigmoid because it avoids the vanishing gradient problem, which can hinder training in deep networks.

After multiple convolutional layers, pooling layers are introduced to reduce the spatial dimensions of the feature maps, which helps decrease computational requirements and prevent overfitting. The most commonly used pooling operation in CNNs is max-pooling, which takes the maximum value from a local region of the feature map, effectively down-sampling the data while retaining the most important features. For example, a 2x2 max-pooling operation would reduce a 4x4 feature map to a 2x2 map by selecting the maximum value from each 2x2 region. Pooling layers help to make the CNN more robust to translations and distortions in the input by focusing on the most dominant features.

After the convolutional and pooling layers, the CNN transitions to fully connected layers, where the learned features are aggregated for the final classification task. These layers take the high-level features extracted by the convolutional layers and map them to the output classes. The final layer typically uses the softmax activation function, which converts the raw scores into probabilities, ensuring that the outputs sum to 1. Softmax not only normalizes the output but also emphasizes the correct class by assigning it the highest probability, making it useful for classification tasks.

An important aspect of CNN architecture is understanding how these various components—convolution, activation, pooling, and fully connected layers—work together to learn from data. CNNs are designed to capture hierarchical representations of input data, starting with low-level features like edges and progressing to more complex patterns as the network deepens. This hierarchical feature learning is what makes CNNs particularly effective for image classification tasks, where the spatial arrangement of pixels holds vital information about the objects in the image.

The mathematical operation of convolution between a kernel/filter $\mathbf{K}$ and an input $\mathbf{X}$ can be expressed as:

$$ \mathbf{Z}(i, j) = \sum_{p=0}^{k-1} \sum_{q=0}^{k-1} \sum_{r=0}^{c-1} \mathbf{X}(i+p, j+q, r) \cdot \mathbf{K}(p, q, r), $$

where $\mathbf{Z}(i,j)$ represents the output of the convolution at spatial location $(i, j)$, $k \times k$ is the kernel/filter size, and $c$ is the number of channels (e.g., RGB channels in images). The result is a feature map that highlights specific patterns in the input, such as edges, textures, or more complex shapes.

CNNs differ from fully connected networks in that:

• They take advantage of local receptive fields, where each neuron is connected to only a small region of the input, preserving spatial structure.

• Parameter sharing is employed, meaning the same filter is applied across different regions of the input, which drastically reduces the number of parameters and improves generalization.

• Pooling layers (such as max-pooling or average-pooling) down-sample feature maps, reducing their spatial dimensions and computational complexity.

Pooling layers typically reduce the dimensionality of the feature maps while retaining the most salient information. For example, max-pooling selects the maximum value from a local patch in the feature map, while average-pooling computes the average value.

The key advantage of CNNs is their ability to learn spatial hierarchies of features, which is crucial for tasks like image recognition. By stacking convolutional layers followed by pooling layers, CNNs can detect increasingly complex patterns in data.

The depth of neural networks allows them to learn hierarchical and abstract representations from data. This is particularly beneficial in tasks such as image classification, where low-level features like edges are combined to form mid-level structures like textures or corners, and eventually high-level features like object parts or complete objects. This hierarchy of learned features is critical to the success of DNNs in domains such as vision, speech, and language.

However, training deep architectures can be challenging due to the vanishing gradient problem, where gradients become extremely small as they are propagated back through many layers. This hampers learning in the early layers of the network. One solution to this problem is the use of the ReLU (Rectified Linear Unit) activation function, which mitigates the vanishing gradient issue by allowing gradients to propagate effectively through layers where activations are positive:

$$ \text{ReLU}(z) = \max(0, z). $$

Another approach is batch normalization, which normalizes the activations of each layer to ensure a stable distribution of inputs to each subsequent layer, accelerating training and reducing the risk of vanishing gradients.

Convolutional layers are the core components of CNNs. By applying filters over local regions of the input, CNNs can detect patterns like edges, corners, and textures. These local features are invariant to translation (i.e., the exact position of the feature within the input), which is a key advantage in tasks like object recognition.

The use of parameter sharing in convolutional layers reduces the number of parameters significantly compared to fully connected layers. Instead of learning a separate weight for each input-pixel connection, a filter learns a single set of parameters that is applied across the entire input. This not only reduces computational cost but also improves the generalization of the model.

Pooling layers further reduce the dimensionality of the feature maps while retaining the most important information. Max-pooling, for instance, selects the maximum value from a small region of the feature map, preserving the strongest activations, which are often the most informative.

Despite their power, deep networks come with several challenges:

• Vanishing gradients: As discussed, gradients can become very small in deep networks, particularly when using activation functions like the sigmoid or tanh, where derivatives saturate for large inputs.

• Overfitting: Deep networks have a large number of parameters, making them prone to overfitting, especially when training on small datasets. Regularization techniques like dropout and L2 regularization help mitigate this issue.

• Computational complexity: Training deep networks requires significant computational resources, both in terms of memory and processing power. Optimizers like Adam and learning rate scheduling can help manage these challenges.

LeNet-5 is one of the most well-known CNN architectures, originally developed by Yann LeCun for the task of digit recognition on the MNIST dataset. The architecture consists of two convolutional layers, two pooling layers, and three fully connected layers. LeNet-5 is widely considered a foundational architecture that demonstrates the power of CNNs for image classification tasks.

In Rust, using the tch-rs crate, we can implement the LeNet-5 architecture and apply it to MNIST classification. Below is the complete implementation:

use tch::{nn, nn::OptimizerConfig, Tensor};

struct LeNet5 {
    conv1: nn::Conv2D,
    conv2: nn::Conv2D,
    fc1: nn::Linear,
    fc2: nn::Linear,
    fc3: nn::Linear,
}

impl LeNet5 {
    fn new(vs: &nn::Path) -> Self {
        let conv1 = nn::conv2d(vs, 1, 6, 5, Default::default());   // 1 input channel (grayscale), 6 filters, 5x5 filter size
        let conv2 = nn::conv2d(vs, 6, 16, 5, Default::default());  // 6 input channels, 16 filters, 5x5 filter size
        let fc1 = nn::linear(vs, 16 * 4 * 4, 120, Default::default()); // Fully connected layer
        let fc2 = nn::linear(vs, 120, 84, Default::default());    // Fully connected layer
        let fc3 = nn::linear(vs, 84, 10, Default::default());     // Fully connected layer, 10 classes for MNIST digits
        LeNet5 { conv1, conv2, fc1, fc2, fc3 }
    }

    fn forward(&self, x: &Tensor) -> Tensor {
        let x = x.view([-1, 1, 28, 28]);  // Reshape input for grayscale 28x28 MNIST images
        let x = x.apply(&self.conv1).relu().avg_pool2d_default(2);  // First conv layer with average pooling
        let x = x.apply(&self.conv2).relu().avg_pool2d_default(2);  // Second conv layer with average pooling
        let x = x.view([-1, 16 * 4 * 4]);  // Flatten the tensor for fully connected layers
        let x = x.apply(&self.fc1).relu();  // First fully connected layer
        let x = x.apply(&self.fc2).relu();  // Second fully connected layer
        x.apply(&self.fc3)  // Output layer for classification
    }
}

fn main() {
    // Load the MNIST dataset
    let mnist = tch::vision::mnist::load_dir("data").unwrap();
    let vs = nn::VarStore::new(tch::Device::Cpu);
    let net = LeNet5::new(&vs.root());

    let mut opt = nn::Adam::default().build(&vs, 1e-3).unwrap();  // Adam optimizer

    // Training loop
    for epoch in 1..10 {
        let loss = net.forward(&mnist.train_images).cross_entropy_for_logits(&mnist.train_labels);
        opt.backward_step(&loss);
        println!("Epoch: {}, Loss: {}", epoch, loss.to_kind(tch::Kind::Float));
    }

    // Test the model's accuracy on the test set
    let test_accuracy = net.forward(&mnist.test_images).accuracy_for_logits(&mnist.test_labels);
    println!("Test Accuracy: {:.2}%", 100.0 * test_accuracy.to_kind(tch::Kind::Float));
}

Deep neural networks (DNNs) and convolutional neural networks (CNNs) are powerful architectures for learning complex, hierarchical representations from data. DNNs, through their depth, enable the extraction of increasingly abstract features, while CNNs exploit spatial hierarchies through convolutional operations, making them highly effective for tasks like image classification.

While the depth of these networks is key to their success, training deep architectures presents challenges such as the vanishing gradient problem and overfitting. Techniques like ReLU activation, batch normalization, and optimizers like Adam help mitigate these challenges. CNN architectures like LeNet-5 showcase the power of convolutional operations for image classification tasks such as MNIST digit recognition, demonstrating both the efficiency and effectiveness of these architectures.

8.6. Evaluation and Hyperparameter Tuning link

In machine learning, the effectiveness of neural network models depends not only on their architectures but also on how they are evaluated and tuned. Evaluation metrics provide insight into a model’s performance, allowing for quantitative comparison across different models and parameter settings. Hyperparameter tuning further optimizes the model's performance by adjusting key factors such as learning rate, batch size, and regularization.

Evaluating a neural network model is essential to understanding its generalization ability, that is, how well it performs on unseen data. Evaluation helps quantify the performance using various metrics depending on the task at hand, such as classification or regression. Once a model is evaluated, hyperparameter tuning is employed to fine-tune the parameters that cannot be learned directly from the data, such as the learning rate, batch size, and regularization terms. The goal is to find the optimal combination of these hyperparameters that maximizes the model's performance.

For a neural network, the evaluation metrics differ depending on whether the task is classification or regression. Each metric gives a different perspective on how well the model is performing with respect to its predictions and their alignment with the true labels.

Classification tasks involve predicting discrete labels, and several metrics are used to evaluate the quality of predictions:

Accuracy measures the proportion of correct predictions over all predictions. Given $n$ data points, where $\mathbf{y}_i$ is the predicted label and $\mathbf{t}_i$ is the true label, accuracy is given by:

$$ \text{Accuracy} = \frac{1}{n} \sum_{i=1}^{n} \mathbb{I}(\mathbf{y}_i = \mathbf{t}_i), $$

where $\mathbb{I}$ is an indicator function that returns 1 if the predicted label matches the true label and 0 otherwise.

Precision is the proportion of true positives among all predicted positives. It evaluates how many of the predicted positive instances are actually correct. For binary classification:

$$ \text{Precision} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Positives}}. $$

Recall (also known as sensitivity or true positive rate) measures the proportion of true positives out of all actual positives. It focuses on how well the model captures the actual positive instances:

$$ \text{Recall} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Negatives}}. $$

F1 Score combines precision and recall into a single metric, particularly useful when dealing with imbalanced datasets. It is the harmonic mean of precision and recall:

$$ \text{F1 Score} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}. $$

Regression tasks involve predicting continuous values, and the evaluation metrics differ from those used in classification:

Mean Squared Error (MSE) is the average of the squared differences between the predicted values $\mathbf{y}_i$ and the true values $\mathbf{t}_i$. It penalizes larger errors more significantly, making it a commonly used metric in regression tasks:

$$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (\mathbf{y}_i - \mathbf{t}_i)^2.$$

Root Mean Squared Error (RMSE) is simply the square root of the MSE, bringing the units of the error back to the same scale as the original data:

$$ \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (\mathbf{y}_i - \mathbf{t}_i)^2}. $$

Mean Absolute Error (MAE) measures the average of the absolute differences between the predicted and actual values. Unlike MSE, it is less sensitive to large errors:

$$ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |\mathbf{y}_i - \mathbf{t}_i|. $$

Each of these metrics provides different insights into model performance. For example, accuracy might be misleading for imbalanced classification problems, where other metrics like precision, recall, or the F1 score would be more informative.

Hyperparameter tuning is the process of searching for the best combination of hyperparameters that maximizes a model’s performance. Unlike model parameters, which are learned during training, hyperparameters must be set before the training process. Important hyperparameters in neural network training include:

• Learning Rate ($\eta$): The learning rate controls the step size of the parameter updates during gradient descent. A large learning rate might cause the model to converge too quickly to a suboptimal solution, while a small learning rate might slow down training. The update rule for gradient descent with learning rate $\eta$ is: $\theta_{t+1} = \theta_t - \eta \nabla_{\theta} \mathcal{L}(\theta),$ where $\nabla_{\theta} \mathcal{L}(\theta)$ is the gradient of the loss function with respect to the parameters $\theta$.

• Batch Size: The batch size defines the number of samples processed before updating the model parameters. A small batch size leads to more frequent updates with higher variance, while a larger batch size reduces variance in updates but requires more memory. Choosing the right batch size is critical to balancing computational efficiency and convergence.

• Regularization Strength ($\lambda$): Regularization helps prevent overfitting by penalizing large weights. Common regularization methods include L2 regularization, which adds a penalty proportional to the sum of the squared weights: $\mathcal{L}_{\text{reg}} = \mathcal{L}(\mathbf{y}, \mathbf{t}) + \frac{\lambda}{2} \sum_{i=1}^{L} \| W_i \|_2^2.$

• The hyperparameter $\lambda$ controls the trade-off between fitting the training data and regularizing the model to improve generalization.

• Number of Hidden Layers and Neurons: The architecture of the neural network (i.e., the number of hidden layers and the number of neurons per layer) is a crucial hyperparameter. Increasing the number of layers and neurons allows the network to model more complex functions but also increases the risk of overfitting.

Hyperparameter tuning is typically performed using search strategies like grid search or random search. Grid search exhaustively tests all possible combinations of hyperparameters within a defined range, while random search samples random combinations, making it computationally cheaper and often more effective in high-dimensional hyperparameter spaces.

Hyperparameters play a critical role in determining the training dynamics and performance of a neural network. Each hyperparameter affects different aspects of the learning process, and finding the optimal combination is essential for maximizing the network's ability to generalize to unseen data. The learning rate, for instance, directly affects how quickly the model converges, while regularization strength controls the model’s capacity to avoid overfitting.

Evaluation metrics are also tightly linked to hyperparameter selection. For example, if a model’s precision is high but recall is low, adjusting the learning rate or regularization may help improve recall without significantly sacrificing precision. This interplay between evaluation metrics and hyperparameters makes tuning a critical step in building effective models.

In addition, hyperparameter tuning strategies like cross-validation ensure that the model generalizes well to different subsets of the data. In cross-validation, the dataset is split into kkk-folds, and the model is trained on $k-1$ folds and evaluated on the remaining fold. This process is repeated $k$ times, and the evaluation results are averaged to provide a more robust estimate of the model’s performance.

Implementing evaluation metrics and hyperparameter tuning in Rust can be done using the tch-rs crate, which supports tensor operations, neural network modules, and automatic differentiation. Below, we present an implementation of a pipeline for hyperparameter tuning using random search, along with evaluation of classification performance on a neural network trained for a complex dataset.

use tch::{nn, nn::OptimizerConfig, Tensor};
use rand::Rng;

struct NeuralNetwork {
    fc1: nn::Linear,
    fc2: nn::Linear,
    fc3: nn::Linear,
}

impl NeuralNetwork {
    fn new(vs: &nn::Path) -> Self {
        let fc1 = nn::linear(vs, 784, 128, Default::default());
        let fc2 = nn::linear(vs, 128, 64, Default::default());
        let fc3 = nn::linear(vs, 64, 10, Default::default());
        NeuralNetwork { fc1, fc2, fc3 }
    }

    fn forward(&self, x: &Tensor) -> Tensor {
        x.view([-1, 784])
            .apply(&self.fc1).relu()
            .apply(&self.fc2).relu()
            .apply(&self.fc3)
    }
}

// Random search for hyperparameter tuning
fn random_search_hyperparameters() -> (f64, i64, f64) {
    let mut rng = rand::thread_rng();
    let learning_rate = rng.gen_range(0.001..0.01);
    let batch_size = rng.gen_range(32..128);
    let regularization = rng.gen_range(0.0001..0.001);
    (learning_rate, batch_size, regularization)
}

fn evaluate_model(model: &NeuralNetwork, data: &Tensor, target: &Tensor) -> Tensor {
    let output = model.forward(data);
    let accuracy = output.accuracy_for_logits(target);
    accuracy.to_kind(tch::Kind::Float)
}

fn main() {
    let vs = nn::VarStore::new(tch::Device::Cpu);
    let net = NeuralNetwork::new(&vs.root());

    let mnist = tch::vision::mnist::load_dir("data").unwrap();
    let (learning_rate, batch_size, regularization) = random_search_hyperparameters();
    let mut opt = nn::Adam::default().build(&vs, learning_rate).unwrap();

    for epoch in 1..10 {
        let loss = net.forward(&mnist.train_images).cross_entropy_for_logits(&mnist.train_labels);
        opt.backward_step(&loss);
        println!("Epoch: {}, Loss: {}", epoch, loss.to_kind(tch::Kind::Float));
    }

    let test_accuracy = evaluate_model(&net, &mnist.test_images, &mnist.test_labels);
    println!("Test Accuracy: {:?}%", test_accuracy * 100.0);
}

This code implements a simple neural network for the MNIST dataset, a random search strategy for hyperparameter tuning, and an evaluation pipeline for measuring accuracy. The random search generates random combinations of learning rates, batch sizes, and regularization strengths, and the evaluation function computes accuracy on the test dataset.

The evaluation of neural networks is critical for understanding their performance and generalization capabilities, while hyperparameter tuning is essential for optimizing their performance on specific tasks. Classification metrics like accuracy, precision, recall, and the F1 score, along with regression metrics like MSE and RMSE, provide a comprehensive view of a model’s effectiveness. Hyperparameters such as learning rate, batch size, and regularization strength directly affect training dynamics, convergence, and model capacity.

Implementing hyperparameter tuning strategies like grid search or random search, combined with robust evaluation metrics, allows practitioners to optimize neural networks effectively. In Rust, the tch-rs crate provides the tools necessary to build, evaluate, and optimize models using these strategies. By integrating evaluation and hyperparameter tuning into the training pipeline, we can ensure that models are not only accurate but also well-optimized for generalization to new data.

8.7. Conclusion link

Chapter 8 equips you with the knowledge and skills to implement, optimize, and evaluate neural networks for both classification and regression tasks using Rust. Mastery of these techniques will enable you to build sophisticated models capable of solving complex machine learning problems.

8.7.1. Further Learning with GenAI link

These prompts are designed to deepen your understanding of neural networks, backpropagation, and their implementation in Rust.

• Explain the basic structure of a neural network. How do neurons, layers, and activation functions work together to model complex relationships in data? Implement a simple feedforward neural network in Rust and apply it to a binary classification task.

• Discuss the role of activation functions in neural networks. How do functions like ReLU, sigmoid, and tanh introduce non-linearity, and what are their respective advantages and disadvantages? Implement these activation functions in Rust and analyze their effects on a neural network's performance.

• Analyze the concept of backpropagation in neural networks. How does backpropagation use the chain rule to compute gradients, and why is it essential for training neural networks? Implement backpropagation in Rust and use it to train a neural network on a regression problem.

• Explore the importance of gradient descent in optimizing neural networks. How does gradient descent work, and what are the different variants (e.g., batch gradient descent, stochastic gradient descent)? Implement gradient descent in Rust and experiment with different learning rates.

• Discuss the challenges of training deep neural networks. What issues arise when training deep networks (e.g., vanishing gradients), and how can these challenges be addressed? Implement a deep neural network in Rust and experiment with different architectures.

• Analyze the impact of regularization techniques in neural networks. How do techniques like L2 regularization and dropout prevent overfitting, and what are the trade-offs involved? Implement regularization in Rust and compare the performance of models with and without regularization.

• Explore the role of normalization techniques in neural networks. How does batch normalization improve training efficiency and model performance, and what are its limitations? Implement batch normalization in Rust and apply it to a neural network.

• Discuss the architecture and benefits of convolutional neural networks (CNNs). How do convolutional layers extract spatial features from data, and why are CNNs particularly effective for image classification? Implement a CNN in Rust and apply it to a dataset like MNIST.

• Analyze the significance of hyperparameter tuning in neural networks. How do hyperparameters like learning rate, batch size, and number of layers affect model performance, and what are the best practices for tuning them? Implement a hyperparameter tuning pipeline in Rust for a neural network.

• Explore the concept of the loss function in neural networks. How do different loss functions (e.g., mean squared error, cross-entropy) influence the training process, and how should they be chosen based on the task? Implement different loss functions in Rust and experiment with their effects on model training.

• Discuss the role of early stopping in neural network training. How does early stopping prevent overfitting, and what are the best practices for implementing it? Implement early stopping in Rust and apply it to a deep neural network.

• Analyze the concept of overfitting in neural networks. What factors contribute to overfitting, and how can it be mitigated through techniques like regularization, dropout, and data augmentation? Implement these techniques in Rust and compare their effectiveness.

• Explore the differences between shallow and deep neural networks. In what scenarios might a shallow network be preferred over a deep network, and how does the depth of a network impact its learning capacity? Implement and compare shallow and deep networks in Rust on the same dataset.

• Discuss the importance of initialization in neural networks. How do different initialization techniques (e.g., random initialization, Xavier initialization) affect the training process, and what are the best practices for initialization? Implement different initialization methods in Rust and experiment with their effects on model convergence.

• Analyze the role of dropout in neural networks. How does dropout help prevent overfitting by randomly deactivating neurons during training, and what are the trade-offs involved? Implement dropout in Rust and apply it to a neural network model.

• Explore the concept of transfer learning in neural networks. How can pre-trained models be fine-tuned for new tasks, and what are the advantages and challenges of transfer learning? Implement transfer learning in Rust using a pre-trained model and apply it to a new dataset.

• Discuss the role of model evaluation in neural networks. How can metrics like accuracy, precision, recall, and F1 score be used to evaluate model performance, and what are the best practices for interpreting these metrics? Implement an evaluation pipeline in Rust for a neural network model.

• Analyze the significance of learning rate schedules in neural network training. How do techniques like learning rate decay and adaptive learning rates improve model convergence, and what are the best practices for implementing them? Implement learning rate schedules in Rust and experiment with their effects on training.

• Explore the concept of model interpretability in neural networks. How can techniques like feature importance, saliency maps, and SHAP values be used to interpret the decisions made by neural networks? Implement interpretability methods in Rust for a neural network model.

Embrace these challenges as a way to expand your expertise and apply your knowledge to solve complex problems with neural networks and Rust.

8.7.2. Hands On Practices link

These exercises are designed to be challenging and in-depth, requiring you to apply both theoretical knowledge and practical skills in Rust.