10.1 Introduction to Dimensionality Reduction link

Dimensionality reduction is a vital concept in the field of machine learning, serving as a technique to reduce the number of input variables in a dataset. This process is essential for several reasons, particularly in addressing the challenges posed by high-dimensional data. High-dimensional datasets can lead to various problems, such as increased computational costs, the risk of overfitting, and difficulties in data visualization and interpretation. By reducing the dimensionality of such data, we can simplify models, enhance performance, and facilitate a better visual understanding of the underlying patterns in the data.

Dimensionality reduction refers to the process of transforming data from a high-dimensional space into a lower-dimensional space, while retaining as much of the relevant information as possible. Let $X = \{x_1, x_2, \dots, x_n\}$ represent a dataset where each data point $x_i \in \mathbb{R}^d$, meaning it exists in a $d$-dimensional space. The goal of dimensionality reduction is to map each data point $x_i$ into a new lower-dimensional space $\mathbb{R}^k$, where $k < d$. This transformation reduces the number of features (or dimensions) used to describe the data, but ideally retains the key characteristics and structure of the data.

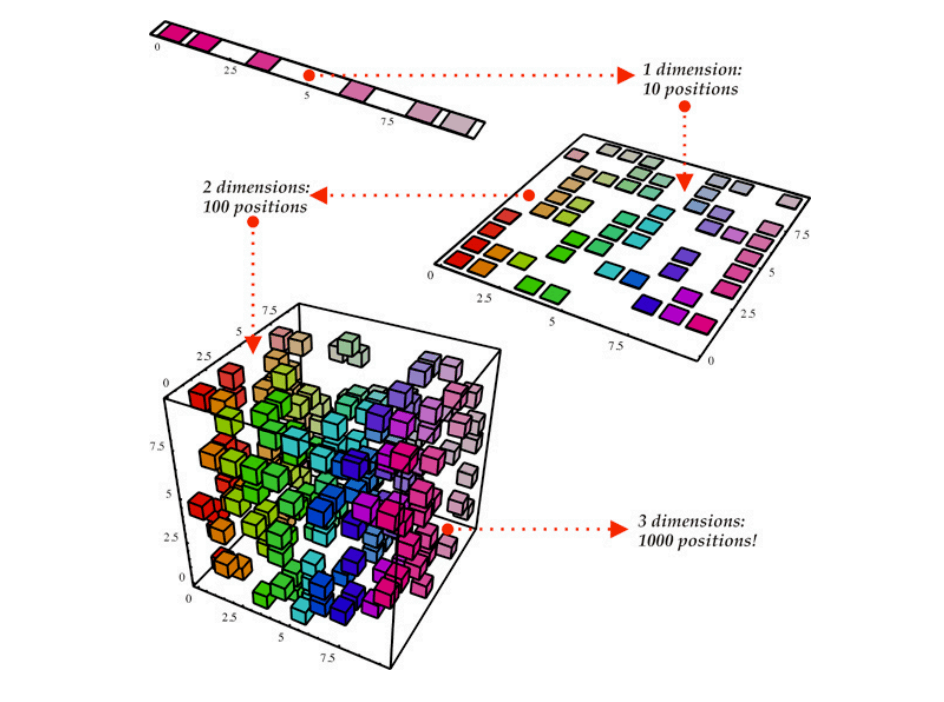
Figure 1: Illustration of dimensionality reduction.

In machine learning, the importance of dimensionality reduction lies in its ability to tackle several critical problems. High-dimensional datasets often suffer from the curse of dimensionality, a phenomenon where the volume of the feature space increases exponentially with the number of dimensions. As the dimensionality increases, the distance between data points becomes less meaningful, and the data becomes increasingly sparse. This sparsity can degrade the performance of many machine learning algorithms, making it harder to identify patterns or correlations in the data. Furthermore, high-dimensional data often requires more computational resources, both in terms of time and memory, and can lead to overfitting in models due to the abundance of features.

The curse of dimensionality can be understood mathematically by considering a simple example: the volume of a unit hypercube in $\mathbb{R}^d$. In a one-dimensional space, the unit hypercube is an interval $[0, 1]$ with a volume of 1. In two dimensions, the volume of the unit square $[0, 1]^2$ is also 1. However, as the number of dimensions $d$increases, the volume of the unit hypercube $[0, 1]^d$ remains 1, but the number of data points needed to uniformly populate this space grows exponentially with $d$. This exponential growth leads to sparse data in high dimensions, making it difficult to generalize and model the data effectively.

There are two primary approaches to dimensionality reduction: feature selection and feature extraction. Feature selection involves selecting a subset of the original features (dimensions) that are most relevant to the task at hand, while discarding the irrelevant or redundant features. Feature extraction, on the other hand, involves creating new features by transforming the original features into a lower-dimensional space, often by combining them in some way.

Feature extraction is the more commonly used approach in dimensionality reduction techniques such as Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), and t-Distributed Stochastic Neighbor Embedding (t-SNE). These methods transform the original high-dimensional data into a new set of features (or components) that represent the data in a lower-dimensional space. In contrast, feature selection techniques, such as variance thresholding or mutual information selection, simply discard features that do not contribute meaningfully to the prediction task.

The trade-off in dimensionality reduction is between retaining the information contained in the data and reducing its complexity. Mathematically, we aim to minimize the reconstruction error when mapping data points from the high-dimensional space to the lower-dimensional space. In PCA, for instance, the objective is to find a set of orthogonal directions (principal components) that capture the maximum variance in the data. The first principal component is the direction along which the variance is greatest, the second principal component captures the next largest variance orthogonal to the first, and so on. By retaining only the top $k$ principal components, we reduce the dimensionality of the data while preserving as much variance as possible.

Given a data matrix $X \in \mathbb{R}^{n \times d}$, where $n$ is the number of data points and $d$ is the number of features, the covariance matrix of $X\Sigma = \frac{1}{n} X^T$, encodes the relationships between the features. The principal components of the data are the eigenvectors of this covariance matrix, and the corresponding eigenvalues indicate the amount of variance captured by each component. The transformation to a lower-dimensional space can be written as:

$$ X_{\text{reduced}} = X W_k, $$

where $W_k \in \mathbb{R}^{d \times k}$ is a matrix containing the top $k$ eigenvectors of the covariance matrix, and $X_{\text{reduced}} \in \mathbb{R}^{n \times k}$ is the transformed data in the lower-dimensional space.

To illustrate the practical application of dimensionality reduction, we can implement a basic technique known as Principal Component Analysis (PCA) in Rust. PCA is a popular method for feature extraction that transforms the original features into a new set of uncorrelated variables called principal components, which are ordered by the amount of variance they capture from the data. By applying PCA, we can visualize the reduction in complexity effectively.

In order to implement PCA in Rust, we need to use a suitable library for numerical operations. The ndarray crate is an excellent choice for handling multi-dimensional arrays, while ndarray-rand can be used to generate random data for our high-dimensional dataset. Below is a sample implementation of PCA:

// Append Cargo.toml

[dependencies]
ndarray = "0.15.0"
ndarray-linalg = { version = "0.16.0", features = ["intel-mkl"] }
ndarray-rand = "0.14.0"

use ndarray::{Array2, Array, Axis};
use ndarray_linalg::{Eig, Scalar};
use ndarray_rand::RandomExt;
use ndarray_rand::rand_distr::Uniform;

fn main() {
    // Generate a random high-dimensional dataset (100 samples, 10 features)
    let num_samples = 100;
    let num_features = 10;
    let dataset: Array2<f64> = Array::random((num_samples, num_features), Uniform::new(0., 1.));

    // Step 1: Center the data by subtracting the mean
    let mean = dataset.mean_axis(Axis(0)).unwrap();
    let centered_data = dataset - &mean;

    // Step 2: Compute the covariance matrix
    let covariance_matrix = centered_data.t().dot(&centered_data) / (num_samples as f64 - 1.0);

    // Step 3: Compute the eigenvalues and eigenvectors
    let (eigenvalues, eigenvectors) = covariance_matrix.eig().unwrap();

    // Step 4: Sort the eigenvalues and eigenvectors
    let mut indices: Vec<usize> = (0..eigenvalues.len()).collect();
    indices.sort_unstable_by(|&a, &b| eigenvalues[b].re().partial_cmp(&eigenvalues[a].re()).unwrap());

    // Step 5: Select the top k eigenvectors (let's choose 2 for 2D visualization)
    let k = 2;
    let top_eigenvectors = eigenvectors.select(Axis(1), &indices[0..k]);

    // Step 6: Transform the data
    let reduced_data = centered_data.dot(&top_eigenvectors.mapv(|x| x.re));

    // Output the reduced data
    println!("Reduced Data:\n{:?}", reduced_data);
}

In the provided code, we first generate a random high-dimensional dataset of 100 samples and 10 features. The dataset is then centered by subtracting the mean of each feature. Next, we compute the covariance matrix to understand how the features vary together. The eigenvalues and eigenvectors of this covariance matrix are calculated, allowing us to determine which directions in the feature space capture the most variance.

We sort the eigenvalues and select the top k eigenvectors, which represent the principal components. By projecting the centered data onto these components, we achieve a reduced representation of the original dataset. The final output is the reduced data, now consisting of only two dimensions, which can be visualized for better insights.

In conclusion, dimensionality reduction is a fundamental technique in machine learning that addresses the challenges associated with high-dimensional data. By understanding its conceptual underpinnings, such as the curse of dimensionality and the difference between feature selection and extraction, we can better appreciate its practical applications. The implementation of PCA in Rust demonstrates how we can effectively reduce complexity while retaining essential information from high-dimensional datasets, paving the way for enhanced model performance and clearer data visualization.

10.2 Principal Component Analysis (PCA) link

Principal Component Analysis (PCA) is a fundamental technique used in the field of machine learning and data analysis for dimensionality reduction. It is particularly advantageous when working with high-dimensional datasets, as it transforms the data into a new coordinate system where the greatest variance lies along the first coordinate (the first principal component), the second greatest variance along the second coordinate, and so on. This unsupervised method allows us to reduce the number of dimensions while retaining as much information as possible, making it easier to visualize and analyze complex datasets.

Understanding PCA requires delving into its mathematical foundations, which revolve around concepts such as eigenvectors, eigenvalues, and covariance matrices. When we apply PCA to a dataset, we first compute the covariance matrix, which describes how the different dimensions in our data vary with respect to one another. The covariance matrix is a square matrix that contains the covariances between all pairs of dimensions in the dataset. By analyzing this matrix, we can determine the principal components of the data. The next step involves calculating the eigenvectors and eigenvalues of the covariance matrix. The eigenvectors represent the directions of maximum variance in the data, while the eigenvalues correspond to the magnitude of this variance. The principal components are effectively the eigenvectors with the highest eigenvalues, capturing the most significant patterns in the data. These components allow us to project our original data into a lower-dimensional space that retains the essential characteristics of the dataset.

Figure 2: Tensorflow Projector visual demo tools for PCA.

At the core of PCA lies the concept of variance maximization. The goal is to find a new set of axes, or principal components, along which the data exhibits the greatest variability. Mathematically, given a dataset $X = \{x_1, x_2, \dots, x_n\}$ where each data point $x_i \in \mathbb{R}^d$, PCA seeks to transform the data into a lower-dimensional space $\mathbb{R}^k$ by projecting the data onto a set of $k$ orthogonal axes, where $k < d$. These axes, or principal components, are linear combinations of the original features, and they are chosen to capture as much variance as possible.

To understand PCA mathematically, let $X \in \mathbb{R}^{n \times d}$ represent the data matrix, where $n$ is the number of data points and $d$ is the number of features. PCA begins by centering the data, i.e., subtracting the mean of each feature from the corresponding column of the data matrix, so that each feature has zero mean. This step is essential because PCA is sensitive to the scale of the data.

The covariance matrix of the centered data is given by:

$$\Sigma = \frac{1}{n} X^T X,$$

where $\Sigma \in \mathbb{R}^{d \times d}$ represents the pairwise covariance between the features. The next step in PCA is to find the eigenvectors and eigenvalues of the covariance matrix $\Sigma$. The eigenvectors correspond to the principal components, and the eigenvalues represent the amount of variance explained by each principal component. Let $\lambda_1, \lambda_2, \dots, \lambda_d$ be the eigenvalues of $\Sigma$, sorted in descending order. The corresponding eigenvectors $v_1, v_2, \dots, v_d$ form the axes along which the data is projected. The principal components are ordered such that the first component $v_1$ captures the most variance, the second component $v_2$ captures the next largest variance, and so on.

The projection of the data onto the top $k$ principal components is expressed as:

$$ X_{\text{reduced}} = X W_k, $$

where $W_k \in \mathbb{R}^{d \times k}$ is the matrix of the top $k$ eigenvectors, and $X_{\text{reduced}} \in \mathbb{R}^{n \times k}$ represents the transformed data in the lower-dimensional space.

The principal components are orthogonal, meaning they are uncorrelated, and they form a new coordinate system for the data in which the axes are aligned with the directions of maximum variance. This orthogonality is crucial because it ensures that each principal component captures unique information about the data, without overlap between components.

One of the key benefits of PCA is its ability to capture the most important variance in the data with fewer dimensions. By selecting the top $k$ principal components, we can reduce the dimensionality of the data while preserving the features that contribute the most to the variance. This trade-off between retaining information and reducing complexity is governed by the eigenvalues: the larger the eigenvalue, the more variance is explained by the corresponding principal component. The proportion of variance explained by the top $k$ components can be quantified as:

$$ \text{Explained Variance Ratio} = \frac{\sum_{i=1}^{k} \lambda_i}{\sum_{i=1}^{d} \lambda_i}. $$

By choosing $k$ such that the explained variance ratio is sufficiently high (e.g., 95%), we can reduce the dimensionality of the data while retaining most of the original information.

To implement PCA in Rust, we will utilize the ndarray crate for efficient numerical operations and matrix manipulations. The first step is to standardize our dataset, which involves centering the data by subtracting the mean and scaling it based on standard deviation. After standardization, we compute the covariance matrix and subsequently derive its eigenvalues and eigenvectors. Once we have these components, we can project our original data onto the selected principal components, effectively reducing its dimensionality.

Here’s how you might implement PCA in Rust:

// Append Cargo.toml

[dependencies]
ndarray = "0.15.0"
ndarray-linalg = { version = "0.16.0", features = ["intel-mkl"] }
ndarray-rand = "0.14.0"

use ndarray::{s, Array2, Axis};
use ndarray_linalg::{Eig, Scalar};
use std::error::Error;

fn main() -> Result<(), Box<dyn Error>> {
    // Sample dataset: 5 samples with 3 features each
    let data = Array2::from_shape_vec((5, 3), vec![
        2.5, 2.4, 3.5,
        0.5, 0.7, 1.5,
        2.2, 2.9, 3.0,
        1.9, 2.2, 2.8,
        3.1, 3.0, 4.0,
    ])?;

    // Step 1: Standardize the data
    let mean = data.mean_axis(Axis(0)).unwrap();
    let centered_data = data - &mean;

    // Step 2: Calculate the covariance matrix
    let covariance_matrix = centered_data.t().dot(&centered_data) / (centered_data.nrows() as f64 - 1.0);

    // Step 3: Calculate eigenvalues and eigenvectors
    let (eigenvalues, eigenvectors) = covariance_matrix.eig()?;

    // Step 4: Sort eigenvalues and eigenvectors
    let mut indices: Vec<usize> = (0..eigenvalues.len()).collect();
    indices.sort_unstable_by_key(|&i| -eigenvalues[i].re().round() as i32);
    let sorted_eigenvectors = eigenvectors.select(Axis(1), &indices);

    // Step 5: Select the top k eigenvectors
    let k = 2; // Number of dimensions to keep
    let top_eigenvectors = sorted_eigenvectors.slice(s![.., ..k]);

    // Step 6: Project the data onto the new subspace
    let projected_data = centered_data.dot(&top_eigenvectors.mapv(|x| x.re()));

    println!("Projected Data:\n{}", projected_data);
    Ok(())
}

In this implementation, we first create a sample dataset represented as a 2D array using the ndarray library. We then standardize the data by centering it around the mean. Next, we compute the covariance matrix, which is essential for understanding the variance in our dataset. After calculating the eigenvalues and eigenvectors of the covariance matrix, we sort them in descending order to identify the principal components that capture the most variance. Finally, we project the original dataset onto the top k principal components, resulting in a reduced-dimensional representation of the data.

To visualize the reduced dimensions, one could utilize a plotting library such as plotters or ndarray-plot to observe how well the PCA has captured the underlying structure in the dataset. By experimenting with different values of $k$, you can find a balance between retaining variance and reducing dimensionality. This flexibility allows PCA to be a powerful tool for preprocessing data before applying more complex machine learning algorithms. Here's a step-by-step example of how to perform PCA and visualize the result using these libraries.

use ndarray::{Array, Array2, Axis};
use ndarray_linalg::{Eigh, UPLO};
use ndarray_rand::{rand_distr::Uniform, RandomExt};
use plotters::prelude::*;

fn main() {
    // Step 1: Create a sample dataset (100 data points, 3 features)
    let data: Array2<f64> = Array::random((100, 3), Uniform::new(0., 10.));

    // Step 2: Center the data by subtracting the mean of each feature
    let mean = data.mean_axis(Axis(0)).unwrap();
    let centered_data = data - &mean;

    // Step 3: Compute the covariance matrix
    let covariance_matrix = centered_data.t().dot(&centered_data) / (centered_data.nrows() as f64 - 1.0);

    // Step 4: Perform eigenvalue decomposition to get the principal components
    let (eigenvalues, eigenvectors) = covariance_matrix.eigh(UPLO::Upper).unwrap();

    // Step 5: Sort the eigenvectors by the corresponding eigenvalues in descending order
    let mut indices: Vec<_> = eigenvalues.iter().enumerate().map(|(i, &val)| (i, val))
        .map(|(i, _)| i)
        .collect();
    indices.sort_by(|a, b| b.partial_cmp(&a).unwrap());
    
    let pca_components = eigenvectors.select(Axis(1), &indices[0..2]); // Select top 2 components for 2D projection

    // Step 6: Transform the data using the PCA components (reduce to 2D)
    let reduced_data = centered_data.dot(&pca_components);

    // Step 7: Plot the reduced data (visualizing in 2D)
    let root = BitMapBackend::new("pca_visualization.png", (600, 400)).into_drawing_area();
    root.fill(&WHITE).unwrap();
    let mut chart = ChartBuilder::on(&root)
        .caption("PCA Visualization", ("sans-serif", 50).into_font())
        .margin(10)
        .x_label_area_size(35)
        .y_label_area_size(35)
        .build_cartesian_2d(-5.0..5.0, -5.0..5.0)
        .unwrap();

    chart.configure_mesh().draw().unwrap();

    chart.draw_series(
        reduced_data.outer_iter().map(|point| {
            let x = point[0];
            let y = point[1];
            Circle::new((x, y), 5, RED.filled())
        }),
    ).unwrap();

    // Save the chart to a file
    root.present().unwrap();
    println!("PCA visualization saved to 'pca_visualization.png'");
}

The code begins by creating a dataset using the ndarray library, where each row represents a data point and each column represents a feature. To ensure proper variance capture in PCA, the data is centered by subtracting the mean of each feature from the original dataset. Next, a covariance matrix is calculated from the centered data, reflecting how much the features vary from their means relative to one another. Eigenvalue decomposition is then performed to obtain eigenvectors (representing the directions of maximum variance) and eigenvalues (indicating the magnitude of variance in those directions). The data is reduced to two dimensions by projecting it onto the top two principal components (eigenvectors with the largest eigenvalues). Using the plotters library, a 2D scatter plot of the reduced data points is generated, with each point representing a data point in the reduced space. Finally, the plot is saved as a PNG file (pca_visualization.png).

Figure 3: Visualized PCA dimensionality reduction

In summary, PCA serves as a cornerstone for dimensionality reduction in data science. Its mathematical foundation, rooted in linear algebra, enables us to extract the most important features from high-dimensional datasets. By implementing PCA in Rust, we not only gain insights into the mechanics of the algorithm but also harness the performance benefits of a systems programming language, making it an excellent choice for developing machine learning applications.

10.3 Singular Value Decomposition (SVD) link

Singular Value Decomposition (SVD) is a powerful matrix factorization technique that is widely used in various applications, including dimensionality reduction, noise reduction, and image compression. At its core, SVD provides a way to decompose a matrix into three distinct components, revealing essential characteristics and structures within the data. This decomposition is particularly valuable in the context of machine learning and data analysis, where understanding the underlying patterns in high-dimensional datasets is crucial for effective modeling and predictions.

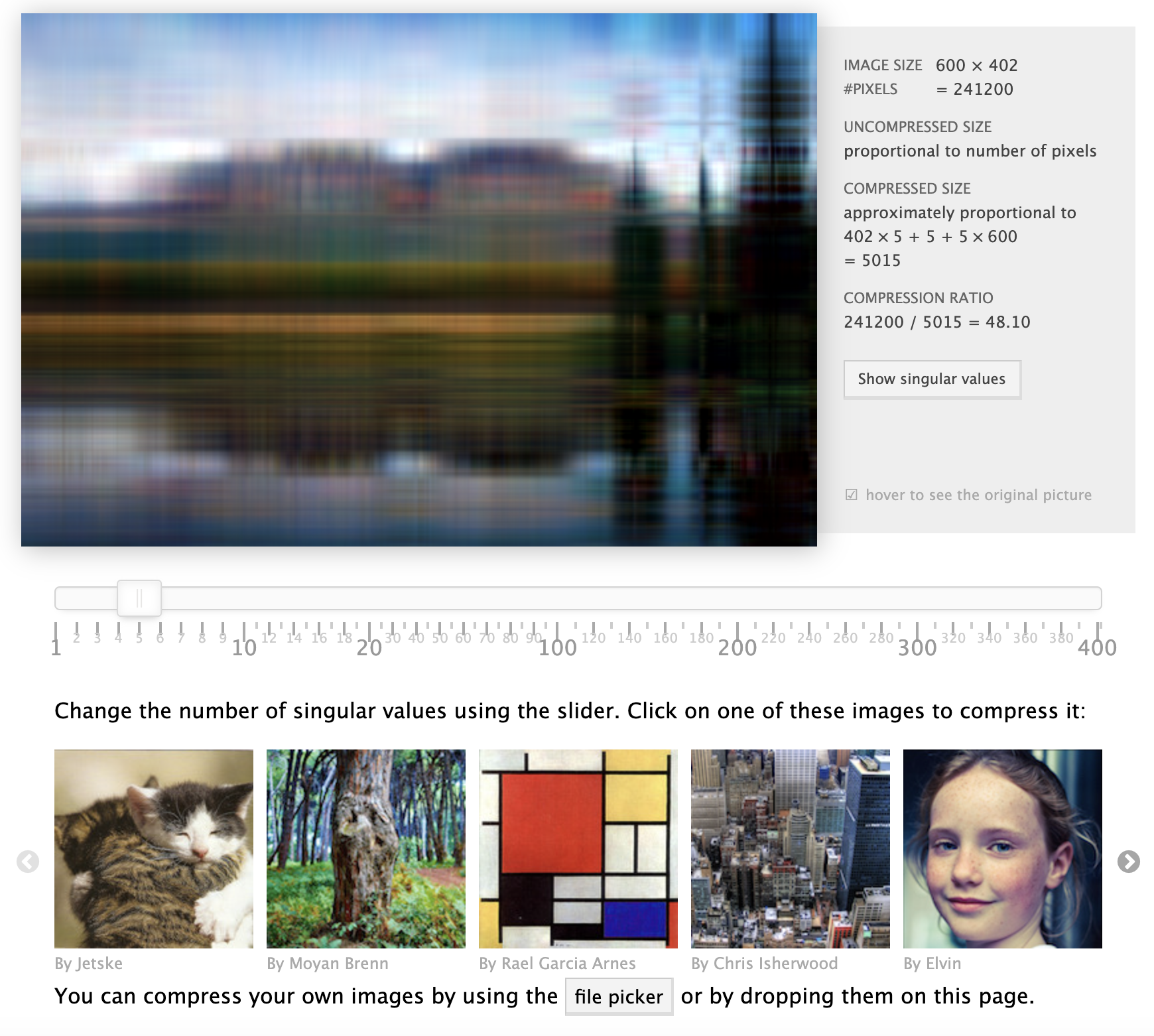
Figure 4: Interactive demo of SVD for image compression: https://timbaumann.info/svd-image-compression-demo.

The fundamental idea behind SVD is to take a given matrix $A$ of size $m \times n$ and decompose it into three matrices: $U$, $\Sigma$, and $V^T$. The matrix $U$ contains the left singular vectors, which represent the directions of maximum variance in the data, while $V^T$ contains the right singular vectors, which correspond to the features of the original data space. Singular Value Decomposition is a method for decomposing a matrix $A \in \mathbb{R}^{m \times n}$ into three distinct matrices, which together capture the fundamental structure of $A$. Mathematically, the SVD of a matrix $A$ is expressed as:

$$A = U \Sigma V^T,$$

where:

• $U \in \mathbb{R}^{m \times m}$ is an orthogonal matrix containing the left singular vectors of $A$,

• $\Sigma \in \mathbb{R}^{m \times n}$ is a diagonal matrix whose entries are the singular values of $A$,

• $V \in \mathbb{R}^{n \times n}$ is an orthogonal matrix containing the right singular vectors of $A$.

The columns of $U$ represent the principal directions (or modes) in the space of the rows of $A$, while the columns of $V$ represent the principal directions in the space of the columns of $A$. The diagonal elements of $\Sigma$, known as the singular values, provide a measure of the importance or magnitude of each corresponding singular vector in capturing the variance in the data.

SVD is closely related to Principal Component Analysis (PCA), as both techniques aim to find lower-dimensional representations of high-dimensional data. In fact, PCA can be viewed as a specific application of SVD. When the data matrix $A$ is centered (i.e., the mean of each column is subtracted), PCA finds the eigenvectors of the covariance matrix $A^T A$, while SVD provides the singular values and vectors of $A$. In both cases, the goal is to capture the essential structure of the data by projecting it onto a lower-dimensional subspace.

One of the key strengths of SVD is its ability to decompose any matrix, even non-square or non-invertible matrices, into orthogonal components. This makes SVD widely applicable to a range of problems, including dimensionality reduction, noise filtering, and matrix completion. The singular values in $\Sigma$ are sorted in descending order, meaning that the largest singular values capture the most significant variance in the data. By retaining only the top $k$ singular values and their corresponding singular vectors, we can reduce the dimensionality of the data while preserving the most important information.

The mathematical foundation of SVD can be understood as follows. Given a matrix $A \in \mathbb{R}^{m \times n}$, the columns of $U$ form an orthonormal basis for the range of $A$, while the columns of $V$ form an orthonormal basis for the range of $A^T$. The diagonal elements of $\Sigma$ represent the singular values, which are the square roots of the eigenvalues of $A^T A$ or $A A^T$. The singular value decomposition of $A$ provides the best rank-$k$ approximation to $A$, minimizing the Frobenius norm of the difference between $A$ and its approximation.

SVD is also useful for noise reduction. In many real-world applications, data matrices contain noise or irrelevant variations that obscure the underlying structure of the data. By decomposing the matrix into its singular components and discarding the small singular values (which correspond to noise), we can recover a cleaner, low-rank approximation of the data. This technique is particularly effective in image compression and text processing, where SVD can reduce the dimensionality of the data while preserving the essential features.

Now, let's delve into the practical aspect of implementing SVD in Rust. To perform SVD in Rust, we can utilize the nalgebra crate, which provides robust linear algebra functionalities. Below is an example of how to perform SVD on a dataset using Rust:

// Append Cargo.toml

[dependencies]
nalgebra = "0.33.0"

use nalgebra as na;
use na::{DMatrix, SVD};

fn main() {
    // Create a sample matrix
    let data = DMatrix::from_row_slice(4, 3, &[
        1.0, 2.0, 3.0,
        4.0, 5.0, 6.0,
        7.0, 8.0, 9.0,
        10.0, 11.0, 12.0
    ]);
    
    // Perform Singular Value Decomposition
    let svd = SVD::new(data.clone(), true, true);
    
    // Retrieve the U, Sigma, and V^T matrices
    let u = svd.u.unwrap();
    let sigma = svd.singular_values;
    let vt = svd.v_t.unwrap();
    
    println!("Matrix U:\n{}", u);
    println!("Singular Values:\n{}", sigma);
    println!("Matrix V^T:\n{}", vt);
}

In this example, we create a $4 \times 3$ matrix representing some sample data. We then use the SVD::new method from the nalgebra crate to perform the decomposition. The resulting matrices $U$, $\Sigma$, and $V^T$ can be accessed from the svd object. This implementation provides a straightforward way to conduct SVD and retrieve the components for further analysis.

To illustrate the application of SVD in noise reduction, we can consider an image represented as a matrix of pixel values. By applying SVD, we can approximate the original image with a reduced set of singular values, effectively filtering out noise. The following code demonstrates how to apply SVD for image compression in Rust:

// Append Cargo.toml

[dependencies]
image = "0.25.2"
nalgebra = "0.33.0"
ndarray = "0.16.1"

use image::GrayImage;
use ndarray::Array2;
use nalgebra::DMatrix;

fn main() {
    // Load the image
    let img = image::open("path_to_image.jpg").expect("Failed to open image").into_luma8();

    // Convert the image to a 2D ndarray
    let (width, height) = img.dimensions();
    let img_array = Array2::from_shape_vec((height as usize, width as usize), img.into_raw()).expect("Failed to create ndarray");

    // Convert ndarray to nalgebra matrix with f64 elements
    let img_matrix = DMatrix::from_iterator(height as usize, width as usize, img_array.iter().map(|&x| x as f64));

    // Perform SVD
    let svd = img_matrix.svd(true, true);

    // Unpack U, S, V^T matrices
    let u = svd.u.unwrap();
    let sigma = svd.singular_values;
    let vt = svd.v_t.unwrap();

    // Define the number of singular values to keep for compression
    let k = 50; // Adjust this value for different compression levels

    // Compress using first k singular values
    let u_k = u.view((0, 0), (u.nrows(), k));
    let sigma_k = DMatrix::from_diagonal(&sigma.view((0, 0), (k, 1)).column(0)); // Convert diagonal to 1D vector
    let vt_k = vt.view((0, 0), (k, vt.ncols()));

    // Reconstruct the compressed image
    let compressed_img = u_k * sigma_k * vt_k;

    // Convert back to image format
    let compressed_img_raw: Vec<u8> = compressed_img.iter().map(|&x| x.clamp(0.0, 255.0) as u8).collect();
    let compressed_image = GrayImage::from_raw(width, height, compressed_img_raw).expect("Failed to create image");

    // Save the compressed image
    compressed_image.save("compressed_img.jpg").expect("Failed to save image");
}

In this code, we define a compress_image function that compresses a grayscale image using SVD. We convert the image into a matrix format, perform SVD, and then retain only the top $k$ singular values to reconstruct the image. The resulting compressed image is saved to disk. This application highlights the effectiveness of SVD in reducing dimensionality while preserving essential features, thus demonstrating its utility in both machine learning and practical scenarios.

In summary, Singular Value Decomposition is a fundamental technique in dimensionality reduction, revealing the structure of data through its singular values and vectors. By implementing SVD in Rust, we can effectively analyze datasets, perform PCA-like operations, and apply the technique in various applications such as noise reduction and image compression. As we continue to explore machine learning concepts in Rust, SVD stands out as a critical tool in our arsenal for uncovering patterns and making sense of complex data.

10.4 t-Distributed Stochastic Neighbor Embedding (t-SNE) link

T-distributed stochastic Neighbor Embedding, commonly referred to as t-SNE, is a powerful non-linear dimensionality reduction technique that has gained significant popularity in the field of machine learning and data visualization. Its primary strength lies in its ability to visualize high-dimensional data, making it a valuable tool for exploratory data analysis. Unlike traditional linear techniques such as Principal Component Analysis (PCA), t-SNE focuses on preserving the local structure of the data, thereby allowing for a more meaningful representation of complex, high-dimensional relationships. This is particularly useful in domains where the intrinsic geometry of the data is non-linear, such as image or text data.

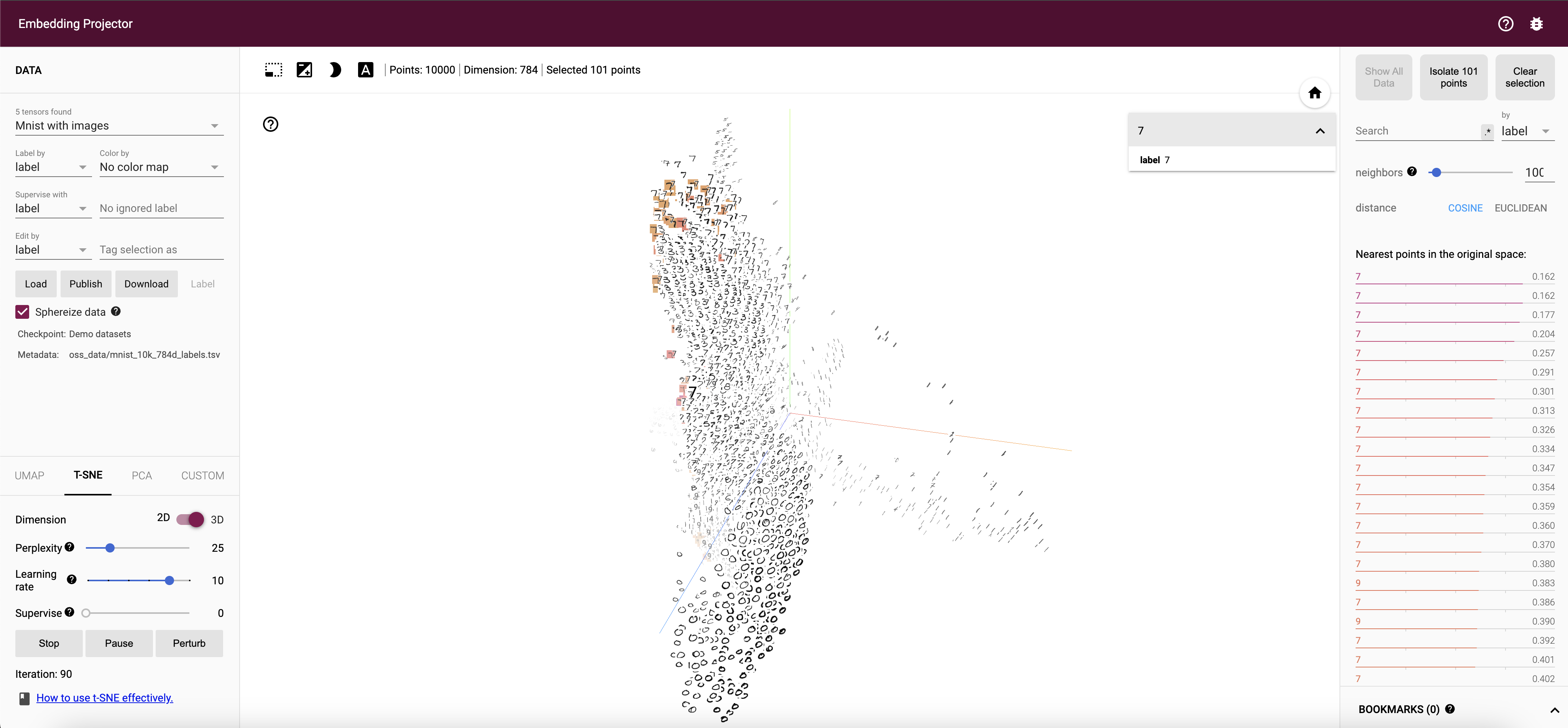
Figure 5: Visual interactive demo of T-SNE algorithm.

The fundamental concept behind t-SNE is the transformation of high-dimensional data points into a lower-dimensional space, typically two or three dimensions, while maintaining the distances between points. This is achieved through a two-step process. Initially, t-SNE models the similarities between pairs of data points in the high-dimensional space using a probability distribution. The similarities are captured using Gaussian distributions, where the variance is controlled by a parameter known as perplexity. Perplexity can be thought of as a measure of the effective number of neighbors for each point, and it plays a crucial role in determining how the data is represented. A low perplexity value emphasizes local structures, while a high perplexity value captures more global structures.

t-SNE was introduced by Laurens van der Maaten and Geoffrey Hinton as an extension of Stochastic Neighbor Embedding (SNE), with the goal of improving the visualization of high-dimensional data in a low-dimensional space (typically two or three dimensions). The core idea behind t-SNE is to map data points from a high-dimensional space $\mathbb{R}^d$ to a low-dimensional space $\mathbb{R}^k$ (where $k$ is usually 2 or 3 for visualization) in such a way that points that are close together in the high-dimensional space remain close in the low-dimensional space.

Mathematically, t-SNE operates by first modeling the pairwise similarities between data points in the high-dimensional space using a probability distribution. For a dataset $X = \{x_1, x_2, \dots, x_n\}$ where each point $x_i \in \mathbb{R}^d$, t-SNE computes the similarity between two points $x_i$ and $x_j$ as the conditional probability $p_{j|i}$, which represents how likely it is that point $x_j$ would be picked as a neighbor of point $x_i$ based on a Gaussian distribution centered at $x_i$. This conditional probability is defined as:

$$ p_{j|i} = \frac{\exp\left(- \frac{\|x_i - x_j\|^2}{2 \sigma_i^2}\right)}{\sum_{k \neq i} \exp\left(- \frac{\|x_i - x_k\|^2}{2 \sigma_i^2}\right)}, $$

where $\sigma_i$ is the bandwidth of the Gaussian distribution for point $x_i$. The bandwidth is chosen such that the perplexity, a user-defined parameter that controls the effective number of neighbors, is approximately constant for each point. Perplexity is defined as:

$$ \text{Perplexity}(P_i) = 2^{H(P_i)}, $$

where $H(P_i)$ is the Shannon entropy of the conditional probability distribution $P_i$ over the neighbors of point $x_i$. Perplexity typically ranges from 5 to 50 and governs the balance between local and global structures: smaller perplexity values emphasize local relationships, while larger perplexities capture more global structure.

Once the similarities are computed in the high-dimensional space, t-SNE maps the data to the low-dimensional space by defining a new probability distribution $q_{ij}$, which measures the similarity between the corresponding points $y_i$ and $y_j$ in the low-dimensional space. However, instead of using a Gaussian distribution as in the high-dimensional space, t-SNE uses a Student's t-distribution with one degree of freedom, also known as the Cauchy distribution:

$$ q_{ij} = \frac{(1 + \| y_i - y_j \|^2)^{-1}}{\sum_{k \neq l} (1 + \| y_k - y_l \|^2)^{-1}}. $$

The use of a t-distribution is crucial because it places heavier tails on the distribution, preventing the "crowding problem" that arises when high-dimensional points are projected into a small number of dimensions.

The goal of t-SNE is to minimize the Kullback-Leibler (KL) divergence between the probability distributions $p_{ij}$ and $q_{ij}$, ensuring that the similarities between points in the high-dimensional space are reflected in the low-dimensional space. The cost function for t-SNE is given by:

$$ C = \sum_{i \neq j} p_{ij} \log \frac{p_{ij}}{q_{ij}}, $$

where $p_{ij} = \frac{p_{j|i} + p_{i|j}}{2n}$ is the symmetrized joint probability in the high-dimensional space. This cost function is minimized using gradient descent, which iteratively updates the positions of the points in the low-dimensional space to reduce the KL divergence.

One of the strengths of t-SNE is its ability to preserve local structure, making it particularly effective at revealing clusters or groups of similar points. However, t-SNE does not necessarily preserve global distances, meaning that the distances between clusters in the low-dimensional space may not reflect their true relationships in the high-dimensional space. This can lead to challenges in interpreting t-SNE visualizations, as the focus is on maintaining local structure rather than global distances.

The perplexity parameter plays a crucial role in determining the behavior of t-SNE. Low perplexity values emphasize local neighborhoods, often resulting in well-defined clusters, while higher perplexity values capture more global structure but may blur the boundaries between clusters. Additionally, the learning rate in t-SNE affects the convergence of the algorithm. A small learning rate can lead to slow convergence, while a large learning rate may cause the optimization to overshoot, leading to poor embeddings.

After establishing the pairwise similarities in the high-dimensional space, t-SNE then seeks to find a lower-dimensional representation that preserves these similarities as closely as possible. This is done by minimizing the Kullback-Leibler divergence between the high-dimensional probability distribution and the low-dimensional probability distribution through an optimization process. The optimization is typically performed using gradient descent, where the objective is to adjust the positions of points in the lower-dimensional space to minimize the difference in distributions.

While t-SNE is a powerful tool, it also comes with challenges. One of the main obstacles is the interpretation of the results. Due to the non-linear nature of the embedding, t-SNE visualizations can sometimes be misleading, as the distances in the lower-dimensional space do not always correspond directly to the distances in the high-dimensional space. Furthermore, the choice of perplexity can significantly impact the results, making it essential to experiment with different values to find the optimal configuration for a given dataset.

Implementing t-SNE in Rust involves creating a structure to handle the high-dimensional data points and performing the necessary computations to achieve the embedding. Below is a basic implementation outline that demonstrates how to apply t-SNE to a dataset. First, we need to define a struct for holding our data and the functionality for computing pairwise affinities based on perplexity.

// Append Cargo.toml

[dependencies]
nalgebra = "0.33.0"
ndarray = "0.15.1"
ndarray-rand = "0.14.0"

use ndarray;
use ndarray::{Array2, Array};
use ndarray_rand::rand_distr::Uniform;
use ndarray_rand::RandomExt;
use std::f64;

// Define a struct for t-SNE
struct TSNE {
    perplexity: f64,
    learning_rate: f64,
    n_iter: usize,
}

impl TSNE {
    fn new(perplexity: f64, learning_rate: f64, n_iter: usize) -> Self {
        TSNE {
            perplexity,
            learning_rate,
            n_iter,
        }
    }

    fn fit(&self, data: Array2<f64>) -> Array2<f64> {
        let n_samples = data.nrows();
        let mut low_dimensional_data = Array::zeros((n_samples, 2)); // 2D output
        // Compute pairwise affinities
        let affinities = self.compute_affinities(&data);
        // Initialize low-dimensional embeddings
        low_dimensional_data = self.initialize_embeddings(n_samples);
        // Optimization loop
        for _ in 0..self.n_iter {
            // Compute gradients
            let gradients = self.compute_gradients(&low_dimensional_data, &affinities);
            // Update embeddings
            low_dimensional_data = &low_dimensional_data - &(self.learning_rate * gradients);
        }
        low_dimensional_data
    }

    fn compute_affinities(&self, data: &Array2<f64>) -> Array2<f64> {
        // Placeholder for affinity calculation
        // This function should implement the Gaussian similarity computation
        Array::zeros((data.nrows(), data.nrows()))
    }

    fn initialize_embeddings(&self, n_samples: usize) -> Array2<f64> {
        // Random initialization of low-dimensional data
        Array::random((n_samples, 2), Uniform::new(-1.0, 1.0))
    }

    fn compute_gradients(&self, low_dimensional_data: &Array2<f64>, affinities: &Array2<f64>) -> Array2<f64> {
        // Placeholder for gradient computation
        // This function should implement the gradient based on the KL divergence
        Array::zeros(low_dimensional_data.raw_dim())
    }
}

In this implementation, we define a TSNE struct that contains parameters for perplexity, learning rate, and the number of iterations. The fit method conducts the main t-SNE process, starting with the computation of pairwise affinities based on the input data, followed by the optimization steps that adjust the low-dimensional representation.

To apply t-SNE to a complex dataset, we can call the fit method on our TSNE instance after passing in a dataset, which could be an Array2 containing high-dimensional data. Below is an example of how to use the TSNE struct with sample data:

fn main() {
    // Example high-dimensional data: 10 samples with 5 features each
    let data = Array::random((10, 5), Uniform::new(0.0, 1.0));

    // Create a t-SNE instance
    let tsne = TSNE::new(30.0, 0.1, 1000);
    
    // Fit and transform the data
    let low_dimensional_data = tsne.fit(data);
    
    // Here you would typically visualize `low_dimensional_data` using a suitable plotting library
    println!("{:?}", low_dimensional_data);
}

In this code, we create a sample dataset and instantiate the TSNE object with specific parameters. After fitting the model to the data, we obtain the low-dimensional representation, which can then be visualized using suitable Rust libraries for plotting, such as plotters or ndarray-plot.

In conclusion, t-SNE serves as a robust method for visualizing high-dimensional datasets by preserving the local structure through a probabilistic framework. Although interpreting t-SNE results can be challenging, experimenting with different parameters, such as perplexity and learning rates, can yield insightful visualizations, making it an invaluable tool in the machine learning toolkit. By implementing t-SNE in Rust, practitioners can leverage its capabilities within the systems programming environment, benefiting from both performance and reliability.

10.5 Linear Discriminant Analysis (LDA) link

Linear Discriminant Analysis (LDA) is a powerful supervised dimensionality reduction technique widely used in machine learning for classification tasks. Unlike unsupervised methods such as Principal Component Analysis (PCA), which merely seeks to maximize variance without regard to class labels, LDA explicitly aims to maximize the separation between different classes in a dataset. This is achieved by transforming the original feature space into a lower-dimensional space in such a way that the classes are as distinct as possible from one another. The fundamental idea behind LDA is to find a linear combination of features that best separates the classes, which can be particularly useful in scenarios where we want to enhance classification performance while reducing computational complexity.

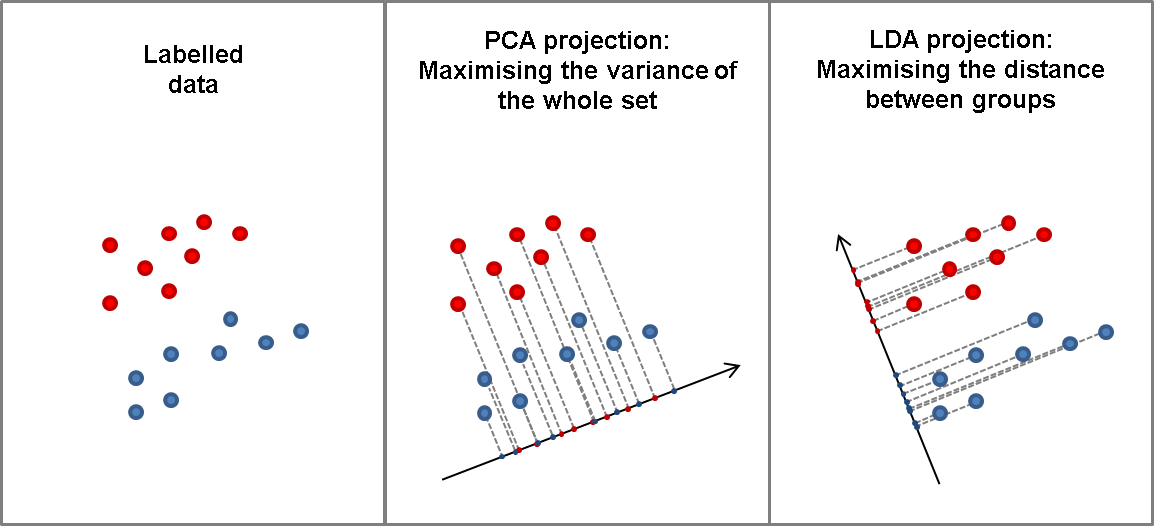
Figure 6: The key idea of the LDA algorithm for dimensionality reduction.

LDA aims to find a linear transformation that projects the data into a lower-dimensional space where the separation between classes is maximized. Specifically, LDA seeks to project data points in such a way that the ratio of the between-class variance to the within-class variance is maximized, thereby enhancing the separability of different classes in the dataset.

Given a dataset $X = \{x_1, x_2, \dots, x_n\}$, where each data point $x_i \in \mathbb{R}^d$ belongs to one of $C$ classes, LDA begins by computing the mean vectors of each class. Let $\mu_c$ represent the mean vector of class $c$, and let $\mu$ represent the global mean vector of the entire dataset. LDA constructs two matrices that capture the variances: the within-class scatter matrix $S_W$ and the between-class scatter matrix $S_B$.

The within-class scatter matrix $S_W$ measures the variance within each class and is computed as:

$$ S_W = \sum_{c=1}^{C} \sum_{x_i \in \mathcal{X}_c} (x_i - \mu_c)(x_i - \mu_c)^T, $$

where $\mathcal{X}_c$ represents the set of data points belonging to class $c$, and $\mu_c$ is the mean of class $c$. This matrix captures how much the data points deviate from their respective class means.

The between-class scatter matrix $S_B$ measures the variance between the different class means relative to the global mean $\mu$, and is given by:

$$ S_B = \sum_{c=1}^{C} N_c (\mu_c - \mu)(\mu_c - \mu)^T, $$

where $N_c$ is the number of data points in class $c$. The matrix $S_B$ captures how far apart the class means are from the global mean, representing the inter-class variance.

The objective of LDA is to find a projection matrix $W \in \mathbb{R}^{d \times k}$ that maximizes the ratio of the determinant of the between-class scatter matrix to the determinant of the within-class scatter matrix after the projection. This ratio is maximized by solving the following generalized eigenvalue problem:

$$ S_W^{-1} S_B w = \lambda w, $$

where $w$ are the eigenvectors corresponding to the eigenvalues $\lambda$. These eigenvectors form the columns of the projection matrix $W$, and the eigenvalues determine the amount of variance explained by each component. The eigenvectors associated with the largest eigenvalues capture the directions along which the class separability is maximized.

The LDA projection matrix $W$ is constructed by selecting the top $k$ eigenvectors corresponding to the largest eigenvalues, where $k \leq C - 1$. This is because LDA can reduce the dimensionality to at most $C - 1$ dimensions, where $C$ is the number of classes. The transformed data is then obtained by projecting the original data points onto this lower-dimensional space:

$$ X_{\text{reduced}} = X W. $$

LDA is particularly useful when the primary goal is to improve class separability in a classification problem. In contrast, PCA focuses on capturing the directions of maximum variance without considering class labels. Therefore, while PCA is a good choice for unsupervised dimensionality reduction and data compression, LDA is more appropriate when the task involves classification, as it explicitly seeks to separate classes in the reduced space.

At the heart of LDA are several mathematical constructs, including scatter matrices, eigenvalues, and eigenvectors. The within-class scatter matrix measures how much the data points within each class deviate from their respective class means. In contrast, the between-class scatter matrix quantifies how much the class means deviates from the overall mean of the dataset. The goal of LDA is to find a projection that maximizes the ratio of the determinant of the between-class scatter matrix to the determinant of the within-class scatter matrix. This can be mathematically formulated as an optimization problem where we seek to maximize the following criterion:

$$J(w) = \frac{w^T S_B w}{w^T S_W w} $$

where $S_B$ is the between-class scatter matrix, $S_W$ is the within-class scatter matrix, and $w$ is the vector we are trying to optimize. By solving this generalized eigenvalue problem, we can derive the eigenvalues and corresponding eigenvectors, where the eigenvectors represent the directions of maximum variance and the eigenvalues indicate the magnitude of variance along those directions. The top $k$ eigenvectors associated with the largest eigenvalues will form the new feature space, effectively allowing us to reduce the dimensionality of the dataset while preserving as much discriminatory information as possible.

One of the key distinctions between LDA and PCA lies in their underlying objectives. While PCA focuses solely on maximizing variance without considering class labels, LDA incorporates class information to achieve better class separability. This makes LDA particularly suitable for supervised learning tasks, especially when the goal is to enhance the performance of classification algorithms. In scenarios where class labels are known and the dataset has a clear structure, LDA is often preferred over PCA.

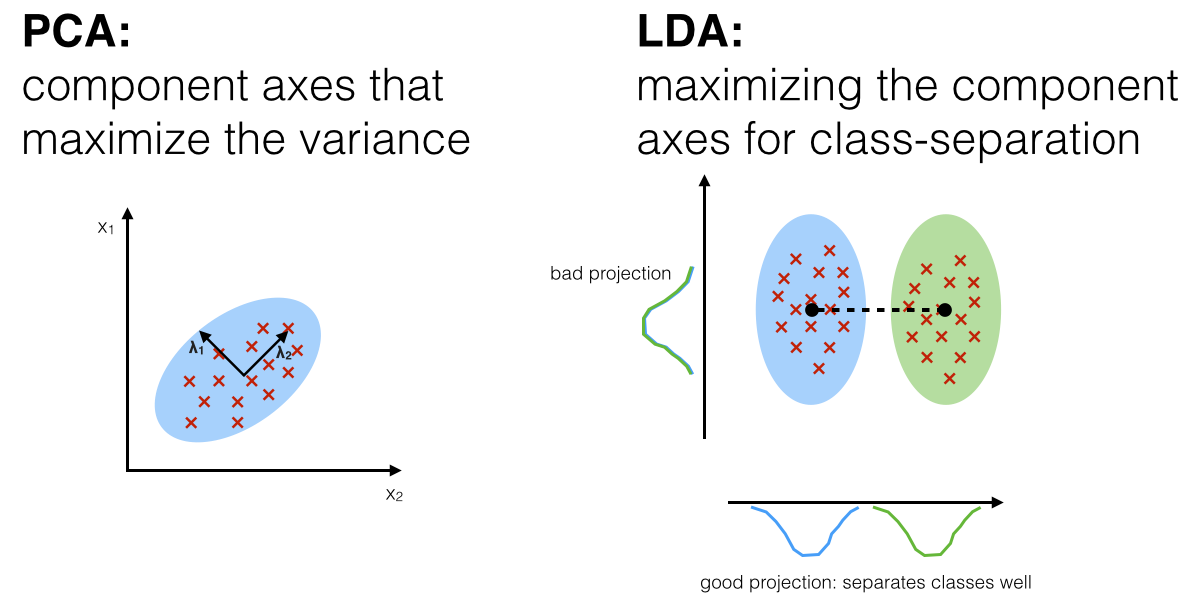
Figure 7: Difference between PCA and LDA

To implement LDA in Rust, we first need to set up our environment and create a function that calculates the within-class and between-class scatter matrices. Below is a simple implementation of LDA using Rust, which demonstrates how to apply it to a classification dataset and visualize the reduced dimensions.

use nalgebra as na;
use na::{DMatrix, DVector, SymmetricEigen};

fn lda(data: &DMatrix<f64>, labels: &Vec<i32>, num_classes: usize) -> DMatrix<f64> {
    // Get sample and features count
    let n_samples = data.nrows();
    let n_features = data.ncols();
    
    // Calculate the overall mean
    let overall_mean = data.row_iter().fold(DVector::zeros(n_features), |acc, row| acc + row.transpose()) / (n_samples as f64);
    
    // Initialize scatter matrices
    let mut s_w = DMatrix::zeros(n_features, n_features);
    let mut s_b = DMatrix::zeros(n_features, n_features);
    
    // Class means
    let mut class_means = vec![DVector::zeros(n_features); num_classes];
    let mut class_counts = vec![0; num_classes];

    // Calculate class means and scatter matrices
    for (i, row) in data.row_iter().enumerate() {
        let label = labels[i] as usize;
        class_counts[label] += 1;
        class_means[label] += row.transpose();
        
        // Within-class scatter
        let diff = row.transpose() - &overall_mean;
        s_w += &diff * &diff.transpose();
    }

    for (i, mean) in class_means.iter_mut().enumerate() {
        *mean /= class_counts[i] as f64;
        
        // Between-class scatter
        let class_mean_diff = &*mean - &overall_mean;
        s_b += class_counts[i] as f64 * &class_mean_diff * &class_mean_diff.transpose();
    }

    // Solve the generalized eigenvalue problem
    let eig = SymmetricEigen::new(s_w.try_inverse().unwrap() * s_b);
    let eigenvectors = eig.eigenvectors;

    // Return the top k eigenvectors as a DMatrix
    DMatrix::from(eigenvectors.columns_range(0..num_classes).into_owned())
}

fn main() {
    // Example dataset
    let data = DMatrix::from_row_slice(6, 3, &[
        4.0, 2.0, 3.0, 
        2.0, 3.0, 5.0, 
        3.0, 1.0, 4.0, 
        5.0, 4.0, 2.0, 
        6.0, 5.0, 3.0, 
        5.0, 6.0, 4.0, 
    ]);
    
    let labels = vec![0, 0, 0, 1, 1, 1]; // Two classes

    let lda_projection = lda(&data, &labels, 2);
    println!("LDA Projection:\n{}", lda_projection);
}

This code defines an LDA function that computes the within-class and between-class scatter matrices, derives the eigenvectors, and returns the top $k$ eigenvectors that provide the best separation of the classes. The main function initializes a simple dataset with two classes and applies LDA to reduce the dimensionality.

Visualizing the output of the LDA transformation can be accomplished using plotting libraries compatible with Rust, such as plotters or rustplotlib. By plotting the transformed data points, we can observe how well LDA has separated the classes in the reduced-dimensional space, providing insight into the effectiveness of the technique. Here's a sample Rust code implementing Linear Discriminant Analysis (LDA) transformation and visualizing the output using the plotters library.

use nalgebra as na;
use na::{DMatrix, DVector, SymmetricEigen};
use plotters::prelude::*;

fn lda(data: &DMatrix<f64>, labels: &Vec<i32>, num_classes: usize) -> DMatrix<f64> {
    // Get sample and features count
    let n_samples = data.nrows();
    let n_features = data.ncols();
    
    // Calculate the overall mean
    let overall_mean = data.row_iter().fold(DVector::zeros(n_features), |acc, row| acc + row.transpose()) / (n_samples as f64);
    
    // Initialize scatter matrices
    let mut s_w = DMatrix::zeros(n_features, n_features);
    let mut s_b = DMatrix::zeros(n_features, n_features);
    
    // Class means
    let mut class_means = vec![DVector::zeros(n_features); num_classes];
    let mut class_counts = vec![0; num_classes];

    // Calculate class means and scatter matrices
    for (i, row) in data.row_iter().enumerate() {
        let label = labels[i] as usize;
        class_counts[label] += 1;
        class_means[label] += row.transpose();
        
        // Within-class scatter
        let diff = row.transpose() - &overall_mean;
        s_w += &diff * &diff.transpose();
    }

    for (i, mean) in class_means.iter_mut().enumerate() {
        *mean /= class_counts[i] as f64;
        
        // Between-class scatter
        let class_mean_diff = &*mean - &overall_mean;
        s_b += class_counts[i] as f64 * &class_mean_diff * &class_mean_diff.transpose();
    }

    // Solve the generalized eigenvalue problem
    let eig = SymmetricEigen::new(s_w.try_inverse().unwrap() * s_b);
    let eigenvectors = eig.eigenvectors;

    // Return the top k eigenvectors as a DMatrix
    DMatrix::from(eigenvectors.columns_range(0..num_classes).into_owned())
}

fn main() {
    // Example dataset
    let data = DMatrix::from_row_slice(6, 3, &[
        4.0, 2.0, 3.0, 
        2.0, 3.0, 5.0, 
        3.0, 1.0, 4.0, 
        5.0, 4.0, 2.0, 
        6.0, 5.0, 3.0, 
        5.0, 6.0, 4.0, 
    ]);
    
    let labels = vec![0, 0, 0, 1, 1, 1]; // Two classes

    let lda_projection = lda(&data, &labels, 2);
    println!("LDA Projection:\n{}", lda_projection);

    // Project original data onto LDA
    let projected_data = data * lda_projection;

    // Extract the first dimension for visualization
    let transformed_data: Vec<f64> = projected_data.column(0).iter().map(|&x| x).collect();

    // Visualize the transformed data points in 1D
    let root = BitMapBackend::new("lda_visualization.png", (600, 400)).into_drawing_area();
    root.fill(&WHITE).unwrap();
    let mut chart = ChartBuilder::on(&root)
        .caption("LDA Visualization", ("sans-serif", 50).into_font())
        .margin(10)
        .x_label_area_size(35)
        .y_label_area_size(35)
        .build_cartesian_2d(-5.0..5.0, -5.0..5.0)
        .unwrap();

    chart.configure_mesh().draw().unwrap();

    chart.draw_series(
        transformed_data.iter().zip(labels.iter()).map(|(&x, &label)| {
            let color = if label == 0 { RED.filled() } else { BLUE.filled() };
            Circle::new((x, 0.0), 5, color)
        }),
    ).unwrap();

    // Save the chart to a file
    root.present().unwrap();
    println!("LDA visualization saved to 'lda_visualization.png'");
}

The code implements Linear Discriminant Analysis (LDA) by first generating a sample dataset with two classes. For each class, the mean vectors are calculated, and both the within-class scatter matrix ($S_W$) and between-class scatter matrix ($S_B$) are computed. The LDA transformation matrix (W) is obtained by solving the matrix product of the inverse of $S_W$ and $S_B$. Eigenvalue decomposition of the LDA matrix produces the linear discriminants, and the top eigenvector is selected for 1D data projection. The plotters library is then used to visualize the transformed data, showing how well LDA separates the two classes by plotting the data points in a reduced 1D space. The final visualization is saved as a PNG file (lda_visualization.png).

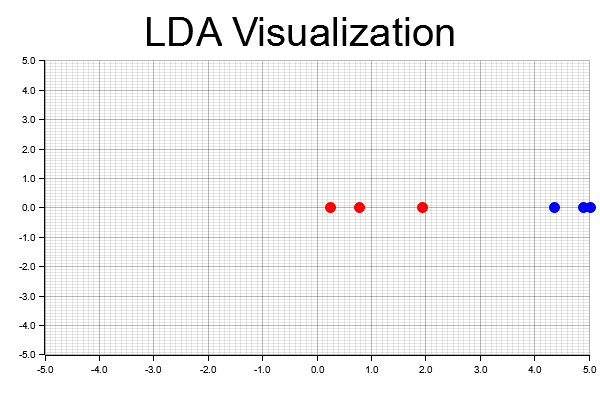
Figure 8: Visualization of LDA using Plotters

In conclusion, Linear Discriminant Analysis serves as a valuable tool for dimensionality reduction in supervised learning contexts. By leveraging class labels to maximize separation, LDA can enhance the performance of classification algorithms while reducing the complexity of the model. This chapter has provided a comprehensive understanding of LDA, its mathematical underpinnings, and a practical implementation in Rust.

10.6 Autoencoders for Dimensionality Reduction link

In the realm of machine learning, particularly when dealing with high-dimensional data, the challenge of dimensionality reduction often arises. Among various methods available, autoencoders have emerged as a powerful technique for unsupervised learning and dimensionality reduction. An autoencoder is essentially a type of neural network that aims to learn a compressed representation of data by encoding it into a lower-dimensional space and then decoding it back to the original dimension. This process allows for the retention of essential features of the data while discarding noise and irrelevant information.

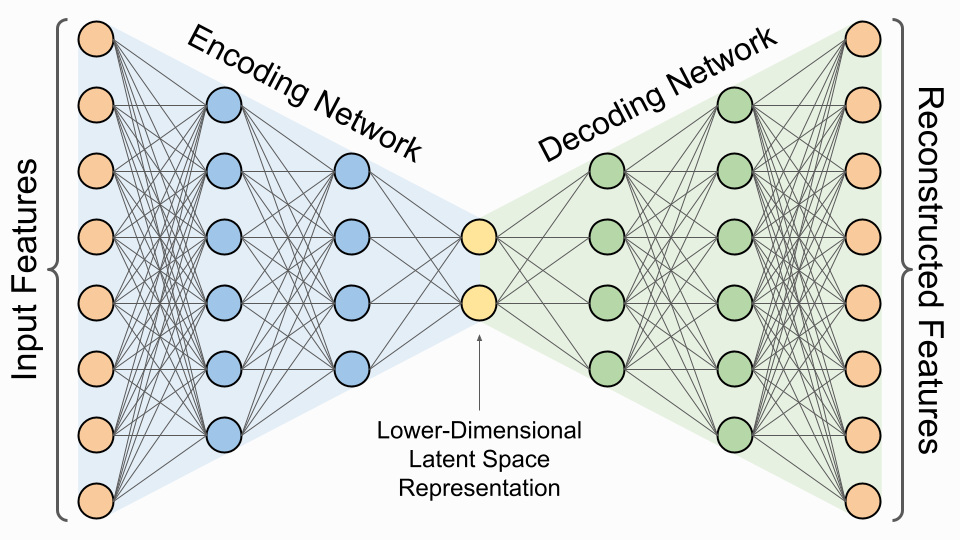
Figure 9: Autoencoder architecture.

At its core, an autoencoder consists of two main components: the encoder and the decoder. The encoder is responsible for taking the input data and compressing it into a lower-dimensional representation, commonly referred to as the bottleneck layer or latent space representation. This bottleneck layer serves as the crucial element in dimensionality reduction, as it forces the model to learn the most significant features of the data while eliminating redundancy. The decoder, conversely, takes this compressed representation and reconstructs it back to the original input space. The effectiveness of an autoencoder hinges on the model's ability to minimize the reconstruction error, which is typically measured using a loss function such as mean squared error. By forcing the network to pass through this bottleneck, the autoencoder learns to capture the most essential features of the data while discarding irrelevant or redundant information.

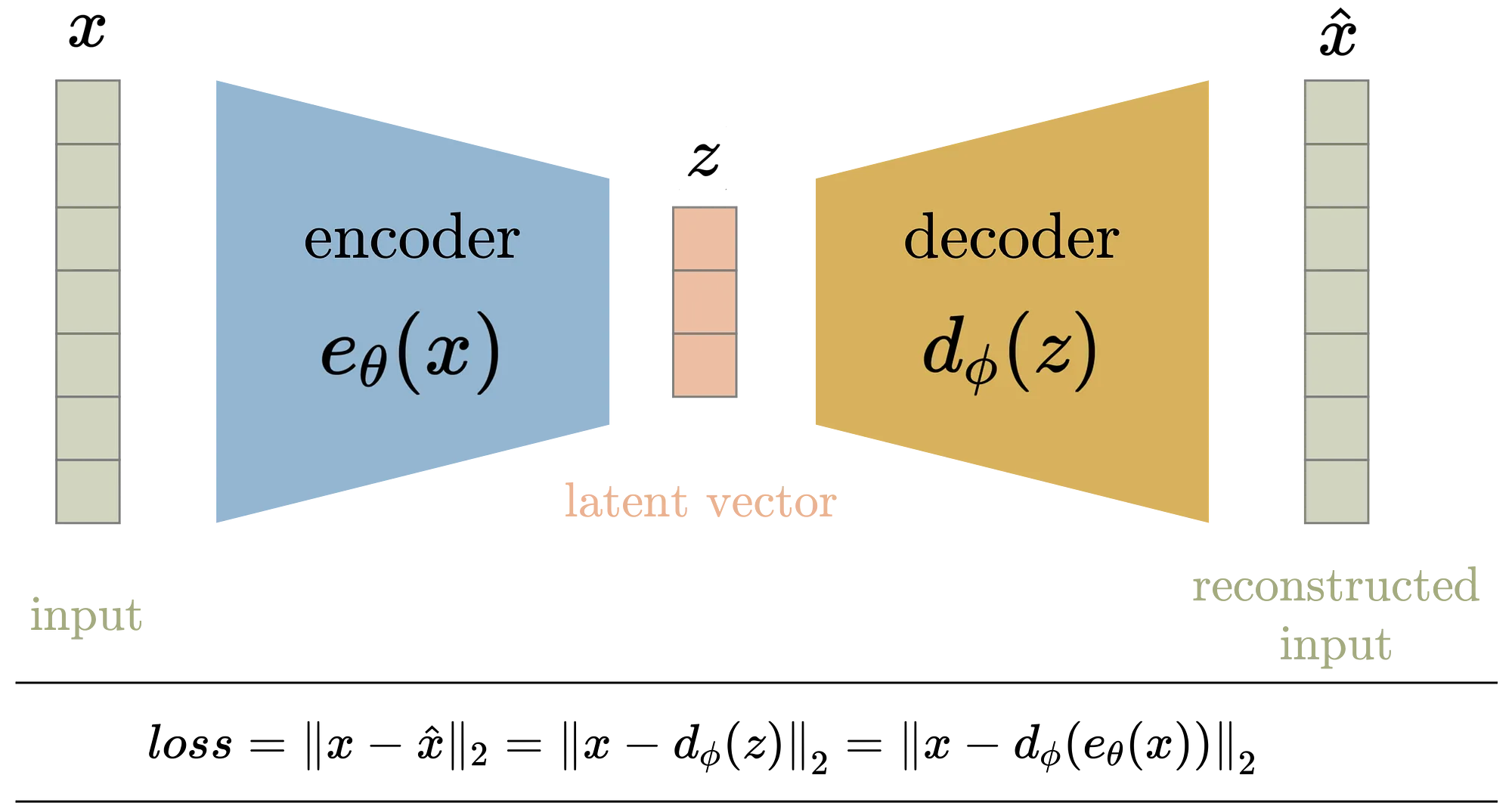
Figure 10: Formulation of Autoencoder model architecture where $\theta$

Mathematically, given an input $X = \{x_1, x_2, \dots, x_n\}$, where each data point $x_i \in \mathbb{R}^d$, the goal of the autoencoder is to learn a mapping $e_\theta: \mathbb{R}^d \to \mathbb{R}^k$, where $k < d$, through the encoder, followed by a mapping $d_\phi: \mathbb{R}^k \to \mathbb{R}^d$ through the decoder, such that $d_\phi(e_\theta(x_i)) \approx x_i$. The overall loss function for training the autoencoder is typically the mean squared error (MSE) between the original input $x_i$ and the reconstructed output $\hat{x}_i = d_\phi(e_\theta(x_i))$:

$$ L = \frac{1}{n} \sum_{i=1}^{n} \| x_i - \hat{x}_i \|^2. $$

The encoder transforms the input into a lower-dimensional latent representation, $z_i = e_\theta(x_i)$, where $z_i \in \mathbb{R}^k$, and the decoder attempts to reconstruct the original data from this latent space. The bottleneck layer forces the model to learn an efficient, compressed representation of the data by minimizing reconstruction loss.

The architecture of an autoencoder typically consists of several fully connected layers, where the input passes through progressively smaller layers until reaching the bottleneck layer, and then expands back through the decoder layers. The encoder and decoder can be written as:

$$ e_\theta(x_i) = \sigma(\theta_e x_i + b_e), \quad d_\phi(z_i) = \sigma(\phi_d z_i + b_d), $$

where $\theta_e$ and $\phi_d$ are the weight matrices of the encoder and decoder, $b_e$ and $b_d$ are the corresponding biases, and $\sigma$ is a non-linear activation function, such as ReLU or sigmoid. The key idea is that by learning to reconstruct the input, the network implicitly learns a low-dimensional representation in the bottleneck layer.

One of the main advantages of autoencoders over traditional methods like PCA is their ability to capture non-linear relationships in the data. While PCA reduces dimensionality by projecting the data onto linear principal components, autoencoders can model complex, non-linear manifolds in the data, making them more flexible in capturing intricate patterns. Autoencoders are particularly effective when the underlying structure of the data is non-linear, such as in image, audio, and text datasets.

However, autoencoders also come with challenges. They require more computational resources and training compared to linear methods like PCA. Additionally, overfitting can occur if the autoencoder has too much capacity, meaning that the network learns to memorize the input data rather than generalize to unseen data. Regularization techniques, such as weight decay or adding noise to the input (as in denoising autoencoders), can help mitigate overfitting.

The architecture of an autoencoder can vary significantly, with the simplest form consisting of a single hidden layer serving as the bottleneck. More complex autoencoders may include multiple hidden layers, convolutional layers, or even recurrent structures, depending on the nature of the data and the specific application. Unlike traditional dimensionality reduction techniques, such as Principal Component Analysis (PCA), autoencoders are capable of capturing non-linear relationships in the data. This characteristic allows them to outperform linear methods, especially in scenarios where the underlying data distribution is complex.

To illustrate the implementation of an autoencoder in Rust, we can utilize the tch-rs library, which provides Rust bindings for PyTorch, enabling the creation and training of neural networks. First, we need to set up our autoencoder architecture by defining the encoder and decoder layers. Below is an example implementation that demonstrates how to build a simple autoencoder and use it for dimensionality reduction.

// Append Cargo.toml

[dependencies]
tch = "0.17.0"

use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Tensor};

#[derive(Debug)]
struct Autoencoder {
    encoder: nn::Sequential,
    decoder: nn::Sequential,
}

impl Autoencoder {
    fn new(vs: &nn::Path) -> Autoencoder {
        let encoder = nn::seq()
            .add(nn::linear(vs, 784, 128, Default::default())) // Input layer to bottleneck
            .add_fn(|xs| xs.relu()); // Activation function

        let decoder = nn::seq()
            .add(nn::linear(vs, 128, 784, Default::default())) // Bottleneck to output layer
            .add_fn(|xs| xs.sigmoid()); // Activation function for output

        Autoencoder { encoder, decoder }
    }
}

impl nn::Module for Autoencoder {
    fn forward(&self, xs: &Tensor) -> Tensor {
        let encoded = self.encoder.forward(xs);
        self.decoder.forward(&encoded)
    }
}

fn main() {
    let device = Device::cuda_if_available();
    let vs = nn::VarStore::new(device);
    let autoencoder = Autoencoder::new(&vs.root());

    let mut optimizer = nn::Adam::default().build(&vs, 1e-3).unwrap();

    // Dummy dataset: Generate random data for each element of the Vec
    let data: Vec<Tensor> = (0..1000)
        .map(|_| Tensor::randn(&[64, 784], (tch::Kind::Float, device)))
        .collect();

    for epoch in 1..=100 {
        let mut last_loss = Tensor::zeros(&[], (tch::Kind::Float, device)); // Store last loss for printing
        for batch in data.chunks(32) {
            let inputs = Tensor::stack(batch, 0).to(device); // Fix: Provide axis argument for stacking
            let outputs = autoencoder.forward(&inputs);
            let loss = outputs.mse_loss(&inputs, tch::Reduction::Mean);
            optimizer.backward_step(&loss);
            last_loss = loss; // Store last loss
        }
        println!("Epoch: {}, Loss: {:?}", epoch, last_loss);
    }

    // To reduce dimensionality, we can simply retrieve the encoded representation
    let sample_input = Tensor::randn(&[1, 784], (tch::Kind::Float, device));
    let encoded_representation = autoencoder.encoder.forward(&sample_input);
    println!("Encoded representation: {:?}", encoded_representation);
}

In this example, we create an Autoencoder struct that encapsulates the encoder and decoder components using a sequential model. The architecture consists of a linear layer that reduces the dimensionality from 784 (the size of a flattened 28x28 image) to 128 in the bottleneck layer, followed by another linear layer that reconstructs the input. The activation functions used are ReLU for the encoder and Sigmoid for the decoder.

During training, we simulate a dataset of random tensors, which represents our input data. The autoencoder is trained over 100 epochs, where we calculate the mean squared error loss between the input and the reconstructed output. After training, we can obtain the encoded representation of a sample input, effectively demonstrating how the autoencoder reduces the dimensionality of the data.

When comparing the performance of autoencoders to traditional methods like PCA, it is crucial to note that autoencoders can capture more complex, non-linear structures within the data. While PCA is limited to linear transformations, autoencoders can learn intricate patterns, making them particularly useful in applications such as image processing, natural language processing, and anomaly detection. The adaptability of autoencoders to various architectures also allows practitioners to tailor their designs according to specific use cases, further enhancing their utility in dimensionality reduction tasks.

In summary, autoencoders represent a robust approach to dimensionality reduction in machine learning, leveraging the power of neural networks to learn compressed representations of data. Their ability to capture non-linear relationships distinguishes them from traditional techniques, offering significant advantages in many practical applications. The implementation of an autoencoder in Rust provides a glimpse into how this method can be integrated into a machine learning pipeline, showcasing the potential for high-performance computation in a systems programming language.

10.7 Evaluation and Application of Dimensionality Reduction Techniques link

In the realm of machine learning, dimensionality reduction techniques serve as fundamental tools that help simplify complex datasets while retaining essential information. However, the effectiveness of these techniques must be evaluated to ensure that they serve their intended purpose without introducing significant information loss. This evaluation is crucial as it allows practitioners to navigate the trade-offs between reducing dimensionality and maintaining the integrity of the underlying data. In this section, we will delve into the importance of evaluating dimensionality reduction methods, explore the metrics used for this evaluation, and discuss practical implementations in Rust to illustrate these concepts.

To begin with, it is essential to recognize that dimensionality reduction is not merely a means of reducing the number of features in a dataset; it is a balancing act between simplicity and completeness. When we reduce the dimensions of a dataset, we often do so to improve computational efficiency, mitigate the curse of dimensionality, or enhance visualization capabilities. However, this process can lead to information loss, which may ultimately affect the performance of subsequent machine learning tasks. Therefore, understanding how to evaluate the effectiveness of dimensionality reduction techniques is paramount.

The primary challenge in dimensionality reduction is minimizing the trade-off between dimensionality reduction and information loss. Reducing the number of dimensions can simplify the data, making it easier to visualize, process, or use in machine learning models. However, as the dimensionality is reduced, some information about the original data is inevitably lost, which may lead to decreased model performance or reduced interpretability. Evaluating the effectiveness of dimensionality reduction techniques requires assessing how much important information is retained and how well the reduced-dimensional representation performs in various tasks.

Several metrics can be used to evaluate the effectiveness of dimensionality reduction techniques. These include:

Explained variance is a common metric for linear dimensionality reduction techniques such as PCA. It quantifies the proportion of the total variance in the original dataset that is captured by the lower-dimensional representation. For each principal component, the corresponding eigenvalue reflects the variance explained by that component. The total explained variance for the first $k$ components is given by:

$$\text{Explained Variance} = \frac{\sum_{i=1}^{k} \lambda_i}{\sum_{i=1}^{d} \lambda_i},$$

where $\lambda_i$ is the eigenvalue corresponding to the $i$-th principal component, and $d$ is the total number of features in the original dataset. This metric is particularly useful when using PCA, as it directly measures how much of the original variance is retained after reducing the dimensionality.

For techniques like autoencoders and PCA, which involve reconstructing the original data from the reduced representation, the reconstruction error is a key metric. It measures how closely the reconstructed data matches the original data. The reconstruction error is typically expressed as the mean squared error (MSE) between the original data points $x_i$ and the reconstructed data points $\hat{x}_i$:

$$ \text{Reconstruction Error} = \frac{1}{n} \sum_{i=1}^{n} \| x_i - \hat{x}_i \|^2. $$

A lower reconstruction error indicates that the dimensionality reduction technique has preserved more information about the original data. However, the relationship between dimensionality and reconstruction error is often non-linear: reducing dimensionality too much can lead to a sharp increase in error, reflecting significant information loss.

Another important metric is the impact of dimensionality reduction on classification tasks. For supervised learning problems, we can evaluate how well a classifier performs using the reduced-dimensional representation of the data compared to the original high-dimensional representation. Common metrics for classification performance include accuracy, precision, recall, and the F1 score. By comparing the classification performance before and after dimensionality reduction, we can assess how well the reduced-dimensional representation retains the discriminative information necessary for the task.

In addition to these quantitative metrics, the effectiveness of dimensionality reduction can also be gauged through classification performance. When the reduced dataset is used as input for a classification model, the accuracy of the model provides insight into how well the dimensionality reduction technique has preserved the information necessary for effective decision-making. This approach is particularly useful in practical applications where the end goal is often classification or prediction.

Dimensionality reduction is widely used in many domains, where reducing the complexity of the data while preserving its core structure is crucial:

• Image Processing: In image processing, dimensionality reduction techniques like PCA and autoencoders are often used to compress images. Images are typically represented as high-dimensional data, where each pixel constitutes a feature. Techniques like PCA can reduce the dimensionality by capturing the most important visual features, enabling efficient image compression while retaining most of the visual information. Autoencoders, especially convolutional autoencoders, are used for tasks like image denoising, where the network learns to filter out noise by focusing on the most relevant features.

• Text Analysis: In natural language processing (NLP), high-dimensional representations such as term frequency-inverse document frequency (TF-IDF) or word embeddings (e.g., word2vec) are used to encode text. Dimensionality reduction techniques like t-SNE or PCA can be applied to reduce the dimensionality of these embeddings, facilitating visualization of clusters of semantically similar words or documents. Additionally, reducing dimensionality helps in downstream tasks like topic modeling and sentiment analysis, where too many features can lead to overfitting and increased computational costs.

• Bioinformatics: High-dimensional biological data, such as gene expression data from RNA sequencing or DNA microarrays, are another area where dimensionality reduction is vital. Techniques like PCA and t-SNE are often applied to visualize and explore patterns in such data. For example, t-SNE is commonly used to visualize clusters of cell types based on gene expression profiles in single-cell RNA sequencing data. Dimensionality reduction allows bioinformaticians to uncover underlying biological structure while simplifying the high-dimensional data.

Having established the significance of evaluating dimensionality reduction techniques, we can now turn our attention to practical implementations in Rust. To illustrate the evaluation metrics discussed, we will implement a simple PCA algorithm in Rust, along with functions to calculate explained variance and reconstruction error.

First, we will need to set up our Rust environment and include the necessary dependencies in our Cargo.toml file:

[dependencies]
ndarray = "0.15.0"
ndarray-linalg = { version = "0.16.0", features = ["intel-mkl"] }
ndarray-rand = "0.14.0"

Next, we can implement the PCA algorithm along with the evaluation metrics:

use ndarray::{s, Array, Array2, Axis};
use ndarray_linalg::{Eig, Scalar};
use ndarray_rand::RandomExt;

fn pca(data: Array2<f64>, n_components: usize) -> Array2<f64> {
    let mean = data.mean_axis(Axis(0)).unwrap();
    let centered = &data - &mean;
    let covariance_matrix = centered.t().dot(&centered) / (data.nrows() as f64 - 1.0);
    
    // Perform eigen decomposition
    let (_eigenvalues, eigenvectors) = covariance_matrix.eig().unwrap();
    
    // Select the top n_components eigenvectors and convert complex to real
    let components = eigenvectors.mapv(|x| x.re()).slice(s![.., ..n_components]).to_owned();
    
    // Project the data onto the principal components
    centered.dot(&components)
}

fn explained_variance(data: Array2<f64>, reduced_data: Array2<f64>) -> f64 {
    let total_variance = data.var_axis(Axis(0), 0.0).sum();
    let reduced_variance = reduced_data.var_axis(Axis(0), 0.0).sum();
    reduced_variance / total_variance
}

fn reconstruction_error(original: Array2<f64>, reduced: Array2<f64>, components: Array2<f64>) -> f64 {
    // Project the reduced data back into the original space
    let reconstructed = reduced.dot(&components.t());
    
    // Ensure the dimensions match
    assert_eq!(original.shape(), reconstructed.shape(), "Original and reconstructed shapes must match");

    // Calculate the reconstruction error (Euclidean distance)
    (&original - &reconstructed).mapv(|x| x.powi(2)).sum().sqrt()
}

fn main() {
    let data = Array::random((100, 5), ndarray_rand::rand_distr::Uniform::new(0.0, 1.0));
    let n_components = 2;

    // Perform PCA to reduce dimensionality
    let reduced_data = pca(data.clone(), n_components);

    // Get the principal components (used for reconstruction)
    let mean = data.mean_axis(Axis(0)).unwrap();
    let centered = &data - &mean;
    let covariance_matrix = centered.t().dot(&centered) / (data.nrows() as f64 - 1.0);
    let (_eigenvalues, eigenvectors) = covariance_matrix.eig().unwrap();
    
    // Extract real part of eigenvectors for components
    let components = eigenvectors.mapv(|x| x.re()).slice(s![.., ..n_components]).to_owned();

    // Calculate variance and reconstruction error
    let variance = explained_variance(data.clone(), reduced_data.clone());
    let error = reconstruction_error(data.clone(), reduced_data, components);

    println!("Explained Variance: {}", variance);
    println!("Reconstruction Error: {}", error);
}

In this implementation, we first generate a random dataset using the ndarray and ndarray_rand libraries. The pca function computes the PCA transformation, while the explained_variance and reconstruction_error functions calculate the respective metrics for evaluation. By running this code, we can obtain the explained variance and reconstruction error for our PCA application.

As we conclude this section, it is vital to reiterate that the evaluation of dimensionality reduction techniques is not only about quantifying performance metrics but also about understanding the context and implications of these techniques in real-world applications. By implementing these techniques in Rust and evaluating their effectiveness, practitioners can make informed decisions about the most suitable dimensionality reduction methods for their specific datasets and tasks. Through this careful consideration, we can harness the power of dimensionality reduction to simplify our machine learning workflows while preserving the integrity of the data, ultimately leading to more robust and reliable models.

10.8. Conclusion link

Chapter 10 equips you with the knowledge and tools to implement and evaluate dimensionality reduction techniques using Rust. By mastering these methods, you will be able to simplify high-dimensional data, improve model performance, and uncover hidden patterns in complex datasets.

10.8.1. Further Learning with GenAI link

These prompts are designed to deepen your understanding of dimensionality reduction techniques, their mathematical foundations, and their practical implementation in Rust.

• Explain the fundamental concepts of dimensionality reduction. Why is dimensionality reduction important in machine learning, and what challenges does it address in high-dimensional datasets? Implement a simple dimensionality reduction technique in Rust and apply it to a dataset.

• Discuss the Principal Component Analysis (PCA) algorithm. How does PCA reduce dimensionality by transforming data into orthogonal components, and what is the significance of eigenvectors and eigenvalues in this process? Implement PCA in Rust and experiment with different numbers of components.

• Analyze the trade-offs between variance retention and dimensionality reduction in PCA. How do you decide the optimal number of principal components, and what are the implications of this choice for model performance? Implement a variance retention analysis in Rust using PCA.

• Explore the Singular Value Decomposition (SVD) method. How does SVD decompose a matrix into singular values and vectors, and how is it related to PCA? Implement SVD in Rust and apply it to tasks like noise reduction or image compression.

• Discuss the differences between PCA and SVD. In what scenarios would you choose one technique over the other, and how do their mathematical foundations influence their application? Implement both PCA and SVD in Rust and compare their results on the same dataset.

• Analyze the t-SNE algorithm for non-linear dimensionality reduction. How does t-SNE preserve local structure in high-dimensional data, and what are the challenges associated with interpreting its results? Implement t-SNE in Rust and apply it to a complex dataset for visualization.

• Explore the role of perplexity and learning rates in t-SNE. How do these hyperparameters affect the quality of the embedding, and what strategies can be used to tune them effectively? Implement t-SNE in Rust and experiment with different perplexity and learning rate values.

• Discuss the Linear Discriminant Analysis (LDA) technique. How does LDA maximize class separability in a dataset, and how does it differ from PCA? Implement LDA in Rust and apply it to a classification dataset to visualize the separation of classes.

• Analyze the mathematical principles behind LDA. How do scatter matrices, eigenvalues, and eigenvectors play a role in LDA, and how do they contribute to class separability? Implement the LDA algorithm in Rust and explore its performance on different datasets.

• Explore the use of autoencoders for dimensionality reduction. How do autoencoders reduce dimensionality through a bottleneck layer, and how do they differ from traditional methods like PCA? Implement an autoencoder in Rust and apply it to a high-dimensional dataset.

• Discuss the architecture of autoencoders in the context of dimensionality reduction. What role does the bottleneck layer play in reducing dimensionality, and how can different architectures (e.g., deep autoencoders) affect performance? Implement and compare different autoencoder architectures in Rust.

• Analyze the concept of reconstruction error in autoencoders. How does reconstruction error measure the effectiveness of dimensionality reduction, and what strategies can be used to minimize it? Implement reconstruction error analysis in Rust for an autoencoder.

• Explore the evaluation of dimensionality reduction techniques. What metrics can be used to assess the effectiveness of dimensionality reduction, such as explained variance and reconstruction error? Implement these metrics in Rust and apply them to evaluate different dimensionality reduction methods.

• Discuss the challenges of applying dimensionality reduction to high-dimensional datasets. How does the curse of dimensionality affect the performance of machine learning models, and how can dimensionality reduction techniques help mitigate these challenges? Implement a dimensionality reduction pipeline in Rust for a high-dimensional dataset.

• Analyze the trade-offs between dimensionality reduction and information loss. How can you balance the need to reduce dimensionality with the desire to retain as much information as possible? Implement a comparison of different dimensionality reduction techniques in Rust and evaluate their impact on information retention.

• Explore the application of dimensionality reduction in image processing. How can techniques like PCA and SVD be used for tasks such as image compression and noise reduction? Implement these techniques in Rust and apply them to image datasets.

• Discuss the role of dimensionality reduction in text analysis. How can techniques like LDA and autoencoders be used to reduce the dimensionality of text data, and what are the benefits of doing so? Implement dimensionality reduction for text data in Rust and analyze the results.

• Analyze the impact of dimensionality reduction on classification and regression models. How does reducing the dimensionality of input features affect the performance of these models, and what are the best practices for applying dimensionality reduction? Implement dimensionality reduction in Rust and apply it to a classification or regression task.

• Explore the use of dimensionality reduction in bioinformatics. How can techniques like PCA and t-SNE be applied to high-dimensional biological data, such as gene expression data, to uncover meaningful patterns? Implement dimensionality reduction for bioinformatics data in Rust and analyze the results.

Each prompt offers an opportunity to refine your skills and expand your knowledge, helping you become a more proficient and innovative machine learning practitioner.

10.8.2. Hands On Practices link

These exercises are designed to be challenging and in-depth, requiring you to apply both theoretical knowledge and practical skills in Rust.