9.1. Introduction to Clustering link

Clustering is a fundamental technique in the field of machine learning that falls under the umbrella of unsupervised learning. Unlike supervised learning, where the model is trained on labeled data, clustering algorithms aim to group similar data points together based on their inherent characteristics without any prior labels. At its core, clustering involves partitioning a dataset into subsets, or clusters, where data points in the same cluster exhibit higher similarity to one another than to those in other clusters. This process enables the extraction of meaningful patterns from data by organizing it into natural groupings.

Clustering algorithms can be broadly categorized into several types, including partitioning methods, hierarchical clustering, density-based clustering, and model-based clustering. Each type offers unique advantages and is suited to different types of data and clustering challenges. For instance, partitioning methods like K-means are straightforward to implement and efficient for large datasets, while hierarchical clustering provides a more flexible approach to explore cluster relationships. On the other hand, density-based methods such as DBSCAN can effectively identify clusters of varying shapes and sizes while being robust to noise, setting them apart from traditional methods that often assume spherical clusters.

The purpose of clustering is multifaceted. It plays a crucial role in various applications, including pattern recognition, customer segmentation, and anomaly detection. In the realm of customer segmentation, businesses leverage clustering to categorize customers based on purchasing behavior, enabling targeted marketing strategies. Similarly, in the domain of anomaly detection, clustering can help identify outliers that deviate significantly from the norm, which is crucial for fraud detection and network security. However, clustering also presents several challenges that practitioners must navigate. One of the most prominent challenges is determining the optimal number of clusters to use, as choosing too few can oversimplify the data while too many can lead to overfitting. Additionally, clustering algorithms must contend with noise in the data, which can obscure the true underlying structure.

At its core, clustering falls under the umbrella of unsupervised learning, distinguishing it from supervised learning. Supervised learning focuses on mapping input data to known output labels, typically through classification or regression tasks. In contrast, unsupervised learning operates without labeled data, aiming instead to uncover hidden structures or patterns within the dataset. Clustering is a prime example of unsupervised learning, where the goal is to group data points into clusters based on their inherent similarities, without prior knowledge of the correct grouping.

Mathematically, let $X = \{ x_1, x_2, \dots, x_n \}$ represent the dataset where $x_i \in \mathbb{R}^d$ is a data point in a ddd-dimensional space. Clustering seeks to partition $X$ into $k$ disjoint subsets (clusters) $C_1, C_2, \dots, C_k$, such that data points within the same cluster are more similar to each other than to those in other clusters. This can be expressed as:

$$ \bigcup_{i=1}^k C_i = X \quad \text{and} \quad C_i \cap C_j = \emptyset \quad \text{for} \quad i \neq j.i=1 $$

The similarity or distance between data points is often measured using metrics like Euclidean distance for numerical data, though alternative measures such as cosine similarity or Manhattan distance may be used depending on the nature of the data and the clustering algorithm.

A variety of clustering algorithms have been developed, each employing different strategies to define and identify clusters. Popular methods include k-means, hierarchical clustering, and density-based clustering. The k-means algorithm, for example, partitions the data into $k$ clusters by iteratively minimizing the within-cluster variance. Hierarchical clustering, on the other hand, constructs a dendrogram by either successively merging or splitting clusters based on a similarity measure. Density-based clustering, such as DBSCAN, groups points based on regions of high density, allowing it to handle noise and discover clusters of arbitrary shape.

The purpose of clustering extends beyond mere data partitioning. It is widely applied in pattern recognition, customer segmentation, and anomaly detection. In pattern recognition, clustering helps to group objects into meaningful categories without explicit labeling. Customer segmentation is a classic use case in marketing, where clustering techniques group customers based on purchasing behavior, allowing for targeted campaigns. Anomaly detection benefits from clustering by isolating outliers or anomalies that do not conform to the patterns of normal data points.

Clustering is not without its challenges. A significant issue is determining the optimal number of clusters, $k$. In k-means, for instance, choosing $k$ can significantly affect the quality of the clusters. Methods like the "elbow method" or silhouette analysis attempt to estimate the appropriate number of clusters, but these are often heuristic and not definitive. Another challenge is handling noise and outliers. Algorithms like DBSCAN are designed to manage noise more effectively by identifying outliers as points that do not belong to any high-density region. Finally, the curse of dimensionality complicates clustering, as high-dimensional spaces can make distance metrics less meaningful, often requiring dimensionality reduction techniques such as Principal Component Analysis (PCA) before clustering.

Figure 1: EduClust interactive visualization for common clustering algorithms.

From a practical standpoint, implementing a clustering algorithm in Rust enables us to gain hands-on experience with the core concepts. Let us consider implementing a basic k-means clustering algorithm. The k-means algorithm begins by randomly initializing $k$ cluster centroids and then iterates over two steps: assigning each data point to the nearest centroid and updating the centroids based on the mean of the points assigned to each cluster. This process repeats until the centroids stabilize, meaning no further changes occur in the cluster assignments.

First, we need to define our data structure. In this example, we will represent a point in a two-dimensional space as a struct:

use rand::{random, seq::SliceRandom};

#[derive(Debug, Clone)]
struct Point {
    x: f64,
    y: f64,
}

Next, we will create a function to calculate the distance between two points. The Euclidean distance is a common choice for this purpose:

fn euclidean_distance(p1: &Point, p2: &Point) -> f64 {
    ((p1.x - p2.x).powi(2) + (p1.y - p2.y).powi(2)).sqrt()
}

Now we can implement the K-means algorithm itself. The function takes a mutable reference to a vector of points, the number of clusters, and performs the clustering:

fn k_means(points: &mut Vec<Point>, k: usize, iterations: usize) -> Vec<Point> {
    let mut centroids: Vec<Point> = points.choose_multiple(&mut rand::thread_rng(), k).cloned().collect();
    let mut assignments: Vec<usize> = vec![0; points.len()];

    for _ in 0..iterations {
        // Assignment step
        for (i, point) in points.iter().enumerate() {
            let mut closest_index = 0;
            let mut closest_distance = euclidean_distance(point, &centroids[0]);
            for j in 1..k {
                let distance = euclidean_distance(point, &centroids[j]);
                if distance < closest_distance {
                    closest_distance = distance;
                    closest_index = j;
                }
            }
            assignments[i] = closest_index;
        }

        // Update step
        for j in 0..k {
            let assigned_points: Vec<&Point> = points.iter().enumerate()
                .filter(|&(index, _)| assignments[index] == j)
                .map(|(_, point)| point)
                .collect();
            if !assigned_points.is_empty() {
                let new_centroid = Point {
                    x: assigned_points.iter().map(|p| p.x).sum::<f64>() / assigned_points.len() as f64,
                    y: assigned_points.iter().map(|p| p.y).sum::<f64>() / assigned_points.len() as f64,
                };
                centroids[j] = new_centroid;
            }
        }
    }

    centroids
}

To visualize the results, we can create a simple main function that generates a dataset of random points and applies the K-means algorithm:

fn main() {
    let mut points: Vec<Point> = (0..100)
        .map(|_| Point {
            x: random::<f64>() * 100.0,
            y: random::<f64>() * 100.0,
        })
        .collect();

    let k = 3; // Number of clusters
    let iterations = 10; // Number of iterations
    let centroids = k_means(&mut points, k, iterations);

    println!("Centroids: {:?}", centroids);
}

This implementation provides a straightforward introduction to clustering principles in Rust, demonstrating how to group data points based on their characteristics. Through this process, we also encounter the challenges and nuances of clustering, such as managing centroid updates and iterating for convergence. Overall, clustering algorithms serve as a powerful tool for data exploration, allowing us to uncover hidden structures in complex datasets.

By bridging the mathematical foundations, conceptual challenges, and practical implementations, this section provides a comprehensive introduction to clustering in machine learning.

9.2. K-Means Clustering link

K-Means is a widely used clustering algorithm that partitions a dataset into K distinct clusters based on feature similarity. The core idea behind K-Means is to identify centroids, which are the center points of each cluster, and iteratively refine the positions of these centroids to achieve optimal clustering. The algorithm works by first initializing K centroids randomly within the data space. Each data point in the dataset is then assigned to the nearest centroid, forming K clusters. After the assignment phase, the algorithm recalculates the centroids by taking the mean of all data points assigned to each cluster. This process of assignment and centroid update is repeated until the centroids stabilize, meaning that the assignments no longer change, or until a predetermined number of iterations is reached.

The iterative nature of K-Means introduces several important concepts such as initialization, assignment, and update. The initialization of centroids can significantly influence the final clusters formed by the algorithm. A poor initialization might lead to suboptimal clustering or slow convergence. Common initialization strategies include random selection and the K-Means++ method, which aims to choose initial centroids that are far apart from each other to improve convergence speed and clustering quality. After initialization, the assignment of each data point to the nearest centroid is performed using a distance metric, typically Euclidean distance. Once all points are assigned, the centroids are updated by calculating the mean of all points in each cluster. This iterative refinement continues until the centroids do not change significantly, indicating that the algorithm has converged.

Choosing the right number of clusters, K, is critical in K-Means clustering. A small K might underfit the data, failing to capture its structure, while a large K may lead to overfitting, resulting in clusters that are too specific and not generalizable. Various methods exist for determining an optimal K, including the elbow method, silhouette score, and cross-validation techniques. Additionally, the K-Means algorithm may face challenges related to convergence, particularly when the dataset contains noise or outliers, or when the clusters have non-spherical shapes. These challenges necessitate careful consideration of both the dataset and the parameters of the K-Means algorithm.

The K-Means algorithm is a fundamental partitioning method that seeks to divide a dataset into $K$ distinct clusters. Given a set of $n$ data points $X = \{x_1, x_2, \dots, x_n\}$, where each data point $x_i \in \mathbb{R}^d$ lies in a $d$-dimensional space, the algorithm aims to find $K$ centroids $\mu_1, \mu_2, \dots, \mu_K$ such that each data point is assigned to the cluster whose centroid is closest to it. Mathematically, the goal is to minimize the sum of squared distances between data points and their corresponding centroids:

$$ \text{arg} \min_{\mu_1, \dots, \mu_K} \sum_{i=1}^{n} \sum_{j=1}^{K} \mathbb{I}(x_i \in C_j) \| x_i - \mu_j \|^2, $$

where $C_j$ is the set of points belonging to cluster $j$, $\mu_j$ is the centroid of cluster $j$, and $\mathbb{I}(x_i \in C_j)$ is an indicator function that is 1 if $x_i \in C_j$ and 0 otherwise. This objective function, often called the within-cluster sum of squares (WCSS), represents the total variance within the clusters.

The K-Means algorithm operates through an iterative refinement process. It begins by initializing $K$ centroids, which can be done randomly or using more sophisticated methods such as the K-Means++ initialization, which chooses centroids to spread out across the dataset. Once the centroids are initialized, the algorithm proceeds in two steps:

• Assignment step: Each data point is assigned to the nearest centroid, based on a distance metric like the Euclidean distance. If $x_i \in \mathbb{R}^d$ is a data point and $\mu_j \in \mathbb{R}^d$ is a centroid, the assignment is determined by:

$$\text{arg} \min_j \| x_i - \mu_j \|.$$

Update step: After the assignment step, the centroids are updated by computing the mean of all data points assigned to each centroid. For cluster $C_j$, the new centroid $\mu_j$ is given by:

$$\mu_j = \frac{1}{|C_j|} \sum_{x_i \in C_j} x_i.$$

These two steps are repeated until the centroids stabilize, meaning that further iterations produce no change in the cluster assignments.

The choice of $K$, the number of clusters, plays a crucial role in the algorithm's performance and outcome. Selecting an appropriate $K$ is often non-trivial and requires domain knowledge or heuristic methods, such as the elbow method or silhouette analysis, to evaluate the quality of the clustering. In the elbow method, the WCSS is plotted as a function of $K$, and the optimal $K$ is chosen at the point where the rate of decrease in WCSS sharply diminishes.

Figure 2: K-Means clustering algorithm and demonstration.

However, K-Means is not without challenges. One of the major issues is the algorithm's sensitivity to initialization. Poorly chosen initial centroids can lead to suboptimal clustering or slow convergence. The K-Means++ initialization, which selects centroids in a way that ensures they are spread out in the dataset, addresses this issue by improving both the speed of convergence and the likelihood of finding a near-optimal solution.

Another challenge is the convergence of the algorithm. Although K-Means is guaranteed to converge, it can converge to a local minimum rather than the global optimum. The algorithm's final result depends heavily on the initial centroid positions, and in practice, it is often necessary to run K-Means multiple times with different initializations and choose the result with the lowest WCSS.

To implement K-Means in Rust, we can create a simple program that performs clustering on a dataset. Below is a basic implementation of the K-Means algorithm. First, we need to define a struct to represent a point in our dataset and another struct to represent the K-Means clustering algorithm.

use rand::Rng;
use std::collections::HashMap;

#[derive(Debug, Clone, PartialEq)]
struct Point {
    x: f64,
    y: f64,
}

#[derive(Debug, Clone)]
struct KMeans {
    k: usize,
    centroids: Vec<Point>,
}

impl KMeans {
    fn new(k: usize) -> Self {
        Self {
            k,
            centroids: Vec::new(),
        }
    }

    fn initialize_centroids(&mut self, points: &[Point]) {
        let mut rng = rand::thread_rng();
        let mut selected_indices = vec![];

        while selected_indices.len() < self.k {
            let index = rng.gen_range(0..points.len());
            if !selected_indices.contains(&index) {
                selected_indices.push(index);
                self.centroids.push(points[index].clone());
            }
        }
    }

    fn assign_clusters(&self, points: &[Point]) -> Vec<usize> {
        points
            .iter()
            .map(|point| {
                self.centroids
                    .iter()
                    .enumerate()
                    .min_by(|(_, a), (_, b)| {
                        let dist_a = self.distance(point, a);
                        let dist_b = self.distance(point, b);
                        dist_a.partial_cmp(&dist_b).unwrap()
                    })
                    .map(|(index, _)| index)
                    .unwrap()
            })
            .collect()
    }

    fn update_centroids(&mut self, points: &[Point], assignments: &[usize]) {
        let mut clusters: HashMap<usize, Vec<Point>> = HashMap::new();

        for (i, &assignment) in assignments.iter().enumerate() {
            clusters
                .entry(assignment)
                .or_insert_with(Vec::new)
                .push(points[i].clone());
        }

        for (i, cluster_points) in clusters {
            let mean_x = cluster_points.iter().map(|p| p.x).sum::<f64>() / cluster_points.len() as f64;
            let mean_y = cluster_points.iter().map(|p| p.y).sum::<f64>() / cluster_points.len() as f64;
            self.centroids[i] = Point { x: mean_x, y: mean_y };
        }
    }

    fn distance(&self, a: &Point, b: &Point) -> f64 {
        ((a.x - b.x).powi(2) + (a.y - b.y).powi(2)).sqrt()
    }

    fn fit(&mut self, points: &[Point]) {
        self.initialize_centroids(points);
        loop {
            let assignments = self.assign_clusters(points);
            let old_centroids = self.centroids.clone();
            self.update_centroids(points, &assignments);

            if old_centroids == self.centroids {
                break;
            }
        }
    }
}

fn main() {
    let dataset = vec![
        Point { x: 1.0, y: 2.0 },
        Point { x: 1.5, y: 1.8 },
        Point { x: 5.0, y: 8.0 },
        Point { x: 8.0, y: 8.0 },
        Point { x: 1.0, y: 0.6 },
        Point { x: 9.0, y: 11.0 },
    ];

    let mut kmeans = KMeans::new(2);
    kmeans.fit(&dataset);
    println!("Centroids: {:?}", kmeans.centroids);
}

In this implementation, we define a Point struct to represent data points in a 2D space. The KMeans struct contains the number of clusters k and a vector to hold the centroids. The initialize_centroids function randomly selects K points from the dataset as initial centroids. The assign_clusters function assigns each data point to the nearest centroid. The update_centroids function recalculates the centroids based on the mean of the points assigned to each cluster. Finally, the fit method orchestrates the entire K-Means process until convergence is reached.

To experiment with different values of K, you can modify the k parameter when creating the KMeans instance. Additionally, you can implement different initialization strategies, such as K-Means++, to enhance the algorithm's performance. Applying K-Means to a real-world dataset, such as customer segmentation in e-commerce or image compression, can provide valuable insights into data patterns and groupings.

In conclusion, K-Means clustering is a powerful algorithm for unsupervised learning, and its implementation in Rust not only demonstrates the language's performance capabilities but also provides a solid foundation for more complex machine-learning tasks. As you continue to explore clustering techniques, consider the implications of K, initialization methods, and the nature of your dataset to optimize the clustering results.

9.3. Hierarchical Clustering link

Hierarchical clustering is a versatile method for grouping data points into clusters based on their similarity. Unlike partitional clustering methods, such as K-Means, which require the number of clusters to be specified in advance, hierarchical clustering builds a hierarchy of clusters without needing to predefine the number of clusters. This approach is divided into two main types: agglomerative and divisive. In agglomerative clustering, a "bottom-up" approach, each data point starts as its own cluster. The algorithm then iteratively merges the closest clusters until a single cluster remains or a desired number of clusters is reached. In contrast, divisive clustering takes a "top-down" approach, beginning with all data points in one cluster and recursively splitting them into smaller clusters.

A key visual tool in hierarchical clustering is the dendrogram, a tree-like diagram that displays the hierarchical relationships between clusters. The dendrogram shows how clusters are merged or split at various levels of granularity, offering insights into the relationships among clusters and the distances at which these clusters are combined. Each branch of the dendrogram represents a cluster, and the height of the branches reflects the distance or dissimilarity at which clusters are joined.

Linkage criteria play a crucial role in hierarchical clustering, determining how the distance between clusters is measured. There are several linkage methods, including single linkage, complete linkage, and average linkage. Single linkage measures the distance between the closest points in two clusters, which can sometimes result in the "chaining effect," where clusters form long, string-like structures. Complete linkage measures the distance between the farthest points in two clusters, producing more compact and tight clusters. Average linkage takes into account the average distance between all points in the clusters, offering a balanced approach between single and complete linkage. The choice of linkage criterion significantly affects the shape and size of the resulting clusters, and selecting the appropriate method depends on the characteristics of the dataset.

Hierarchical clustering offers several advantages over partitional methods. One of its key strengths is the ability to reveal nested cluster structures, allowing researchers to examine the data at multiple levels of granularity without needing to specify the number of clusters upfront. This flexibility makes hierarchical clustering particularly useful for exploring complex data. Additionally, the hierarchical approach provides a comprehensive view of the data, enabling more nuanced interpretations of the relationships among data points.

In agglomerative clustering, the process begins with each data point as its own cluster. These individual clusters are successively merged based on a predefined criterion (such as distance or similarity) until all data points belong to a single cluster. Mathematically, let $X = \{x_1, x_2, \dots, x_n\}$ represent a dataset where $x_i \in \mathbb{R}^d$, and the aim is to iteratively combine clusters $C_1, C_2, \dots, C_k$ into fewer clusters at each step until a complete hierarchy is formed.

Conversely, divisive clustering starts with all data points in one cluster and recursively splits the clusters into smaller groups. While divisive clustering is conceptually appealing, agglomerative clustering is more commonly used due to its simplicity in terms of computation.

One of the core components of hierarchical clustering is the linkage criterion, which determines how the distance between two clusters is defined. Common linkage criteria include:

• Single linkage: The distance between two clusters is defined as the shortest distance between any pair of points, one from each cluster. Mathematically, for clusters $C_i$ and $C_j$, the distance is given by:

$$ d(C_i, C_j) = \min_{x \in C_i, y \in C_j} \| x - y \|. $$

Figure 3: Single linkage algorithm.

• Complete linkage: The distance between two clusters is the longest distance between any pair of points from each cluster:

$$ d(C_i, C_j) = \max_{x \in C_i, y \in C_j} \| x - y \|. $$

Figure 4: Complete linkage algorithm.

• Average linkage: The distance between two clusters is the average of the pairwise distances between all points in the two clusters:

$$ d(C_i, C_j) = \frac{1}{|C_i| |C_j|} \sum_{x \in C_i} \sum_{y \in C_j} \| x - y \|. $$

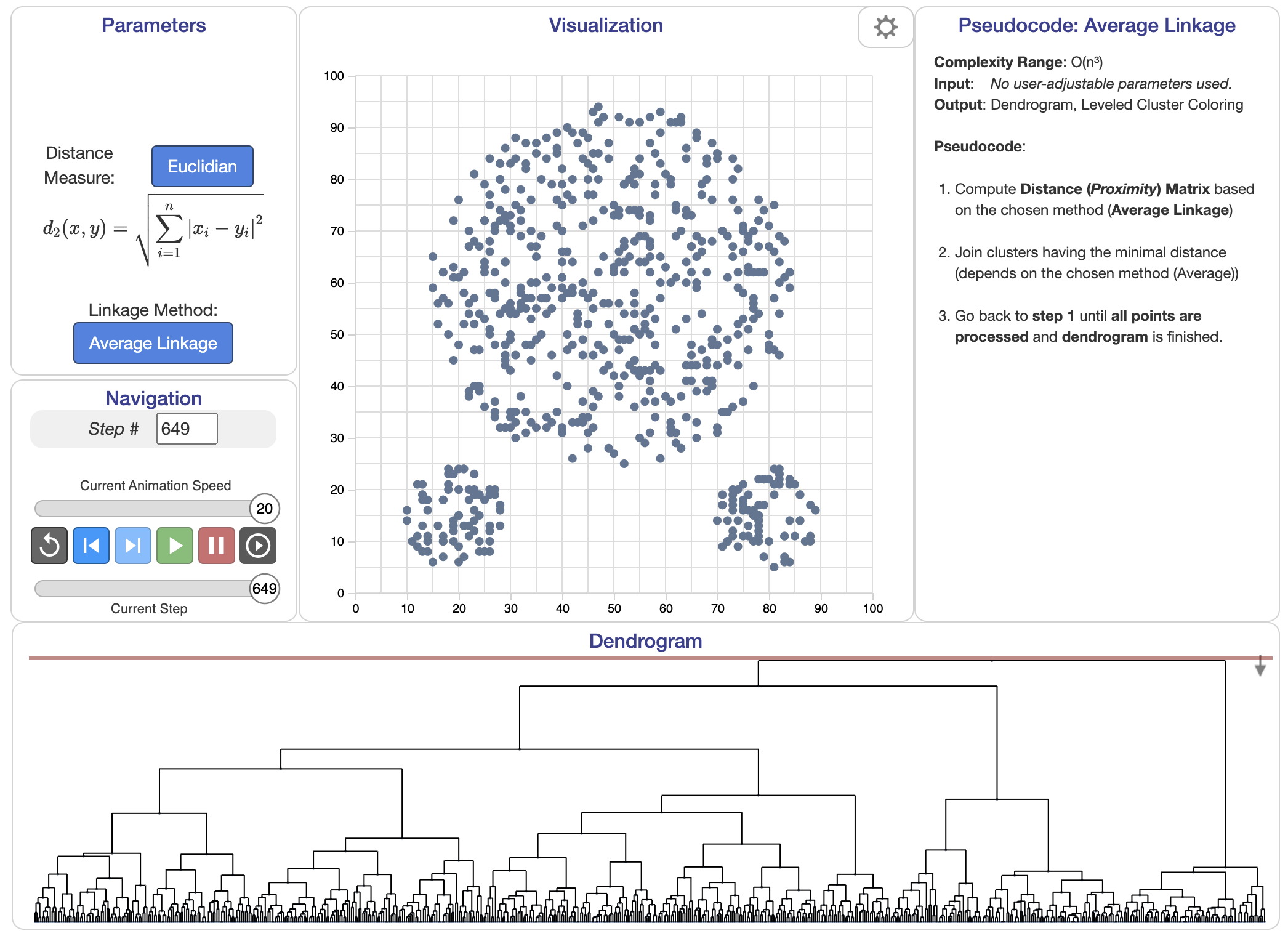
Figure 5: Average linkage algorithm.

Each of these criteria influences the shape and structure of the resulting dendrogram, revealing different aspects of the clustering structure. For example, single linkage tends to produce long, chain-like clusters, while complete linkage tends to generate more compact clusters.

The dendrogram produced by hierarchical clustering is a tree-like structure that represents the nested arrangement of clusters. At the bottom of the dendrogram, each leaf corresponds to an individual data point, while the root represents the entire dataset. As we move up the dendrogram, data points are progressively merged into larger clusters. The height at which two clusters merge reflects the distance or dissimilarity between them. By cutting the dendrogram at a particular level, we can obtain a partitioning of the data into clusters. One of the advantages of hierarchical clustering is its ability to reveal the nested structure of the data, which partitional methods like K-Means cannot do.

Hierarchical clustering is advantageous when we are interested in exploring data at multiple levels of granularity or when the number of clusters is not known in advance. Additionally, hierarchical clustering provides more flexibility in exploring data structure compared to partitional methods. It is particularly useful in fields like biology for phylogenetic tree construction, where nested groupings of species or genes reflect evolutionary relationships. In marketing, hierarchical clustering can be applied to discover customer segments at different levels of specificity.

However, hierarchical clustering also has limitations. The most significant drawback is its computational complexity. For agglomerative clustering, the complexity is typically $O(n^2 \log n)$, which can become infeasible for large datasets. Additionally, once a decision is made to merge or split clusters, it cannot be undone, leading to potentially suboptimal clusters if early decisions were incorrect.

To implement hierarchical clustering in Rust, we need to follow a systematic approach. First, we will create a representation of our data points, typically as a two-dimensional array or vector. Then, we will need to calculate the distance matrix that captures the pairwise distances between all data points. After that, we can apply the agglomerative clustering algorithm based on the chosen linkage criteria. For this example, let’s assume we have a simple dataset of 2D points and we will use a single linkage for our clustering.

Here is a sample implementation of hierarchical clustering in Rust. This code assumes that we have a vector of points represented as tuples:

#[derive(Debug)]
struct Cluster {
    points: Vec<(f64, f64)>,
}

fn euclidean_distance(p1: (f64, f64), p2: (f64, f64)) -> f64 {
    ((p1.0 - p2.0).powi(2) + (p1.1 - p2.1).powi(2)).sqrt()
}

fn calculate_distance_matrix(data: &Vec<(f64, f64)>) -> Vec<Vec<f64>> {
    let n = data.len();
    let mut distance_matrix = vec![vec![0.0; n]; n];
    for i in 0..n {
        for j in i + 1..n {
            let distance = euclidean_distance(data[i], data[j]);
            distance_matrix[i][j] = distance;
            distance_matrix[j][i] = distance;
        }
    }
    distance_matrix
}

fn hierarchical_clustering(data: &Vec<(f64, f64)>) -> Vec<Cluster> {
    let mut clusters: Vec<Cluster> = data.iter().map(|&point| Cluster { points: vec![point] }).collect();
    let mut distance_matrix = calculate_distance_matrix(data);

    while clusters.len() > 1 {
        let mut min_distance = f64::MAX;
        let (mut closest_pair_i, mut closest_pair_j) = (0, 0);

        for i in 0..clusters.len() {
            for j in i + 1..clusters.len() {
                if distance_matrix[i][j] < min_distance {
                    min_distance = distance_matrix[i][j];
                    closest_pair_i = i;
                    closest_pair_j = j;
                }
            }
        }

        let new_cluster = Cluster {
            points: [clusters[closest_pair_i].points.clone(), clusters[closest_pair_j].points.clone()].concat(),
        };

        // Remove clusters j and i, ensure removal of the higher index first
        clusters.remove(closest_pair_j);
        clusters.remove(closest_pair_i);

        // Add new cluster
        clusters.push(new_cluster);

        // Update distance matrix for the new cluster
        let new_cluster_index = clusters.len() - 1;
        distance_matrix.push(vec![0.0; clusters.len()]);

        for k in 0..clusters.len() - 1 {
            let dist = distance_matrix[closest_pair_i][k].min(distance_matrix[closest_pair_j][k]);
            distance_matrix[new_cluster_index][k] = dist;
            distance_matrix[k].push(dist);
        }
    }
    clusters
}

fn main() {
    let data: Vec<(f64, f64)> = vec![
        (1.0, 2.0), (1.5, 1.8), (5.0, 8.0), (8.0, 8.0), (1.0, 0.6), (9.0, 8.0)
    ];

    let clusters = hierarchical_clustering(&data);

    for cluster in clusters {
        println!("{:?}", cluster);
    }
}

In this code, we define a Cluster struct to hold points that belong to a specific cluster. The euclidean_distance function computes the distance between two points, and the calculate_distance_matrix function creates a distance matrix for the dataset. The hierarchical_clustering function implements the agglomerative clustering algorithm, merging clusters based on the minimum distance until only one cluster remains.

To visualize the results, we can create a dendrogram. While Rust does not have as extensive visualization libraries as Python, we can output the merging process and then use tools like Python or R for visualization. The dendrogram can be constructed by keeping track of the merges and distances throughout the clustering process.

Experimenting with different linkage criteria, such as complete or average linkage, can be done by modifying the distance calculation within the hierarchical_clustering function. By applying hierarchical clustering to various datasets, you can observe how the structure of the clusters changes with different linkage criteria and gain insights into the underlying patterns present in the data.

In summary, hierarchical clustering is a versatile and insightful clustering technique that can reveal complex relationships within datasets. Implementing this method in Rust offers opportunities for efficiency and performance, particularly in large-scale applications. The exploration of various linkage criteria and visualizations further enhances our understanding of the data and the clusters formed.

9.4. Density-Based Clustering (DBSCAN) link

Density-Based Spatial Clustering of Applications with Noise, commonly known as DBSCAN, is a powerful clustering algorithm that identifies clusters based on the density of data points in a given space. Unlike traditional clustering methods like K-Means, which assume spherical clusters and require the specification of the number of clusters beforehand, DBSCAN can discover clusters of arbitrary shapes and is particularly adept at handling noise and outliers. This makes it an invaluable tool in various fields, such as image processing, geospatial analysis, and anomaly detection.

One of the primary advantages of DBSCAN over methods like K-Means and hierarchical clustering is its ability to identify clusters of arbitrary shape. K-Means, as mentioned earlier, tends to favor spherical clusters and requires prior knowledge of the number of clusters, while hierarchical methods can produce a nested structure that may not represent the underlying data distribution accurately. DBSCAN, however, can uncover complex structures and is robust to noise, making it highly effective for real-world applications where data does not conform to idealized shapes.

DBSCAN, or Density-Based Spatial Clustering of Applications with Noise, represents a fundamentally different approach from partitional methods like K-Means or hierarchical clustering. Instead of relying on distance metrics or tree structures, DBSCAN identifies clusters by examining the local density of points in a dataset. It does so by defining two essential parameters: $\epsilon$, which specifies the neighborhood radius around each point, and $\text{minPts}$, the minimum number of points required to form a dense region.

At its core, DBSCAN operates on two primary concepts: core points and reachable points. A core point is defined as a point that has at least a specified number of neighboring points (the minPts parameter) within a defined radius (the epsilon parameter). Reachable points are those that can be reached from a core point within a distance of epsilon. This means that if point A is a core point, and point B lies within the epsilon radius from A, then B is considered a reachable point from A. The algorithm also identifies noise points, which are neither core points nor reachable points. These noise points represent outliers in the dataset and are crucial for ensuring that the clusters identified by DBSCAN are valid.

The parameters epsilon and minPts play a significant role in the performance of DBSCAN. The epsilon parameter defines the neighborhood radius around a point, while minPts determines the minimum number of points required to form a dense region. Choosing appropriate values for these parameters is essential for optimizing clustering results. If epsilon is too small, many points may be classified as noise, while if it’s too large, the algorithm may merge distinct clusters into one. Similarly, a small value for minPts may lead to the over-identification of clusters, while a large value may result in under-clustering.

In DBSCAN, points are classified into three categories:

• Core points: A point $p$ is considered a core point if there are at least $\text{minPts}$ points (including $p$) within its $\epsilon$-neighborhood. Mathematically, if $N(p) = \{ q \in X : \| p - q \| \leq \epsilon \}$ is the set of points within distance $\epsilon$ of $p$, then $p$ is a core point if $|N(p)| \geq \text{minPts}$.

• Border points: A point $q$ is a border point if it is within the $\epsilon$-neighborhood of a core point but does not have enough neighbors to itself be a core point.

• Noise points: Any point that is neither a core point nor a border point is classified as noise, meaning it does not belong to any cluster.

The process of DBSCAN begins by randomly selecting a point in the dataset and checking if it qualifies as a core point based on the $\epsilon$ and $\text{minPts}$ parameters. If it is a core point, DBSCAN expands the cluster by recursively adding all density-reachable points, i.e., points that are within the $\epsilon$-neighborhood of core points. This process continues until all points are classified as either core points, border points, or noise.

One of the key advantages of DBSCAN is its ability to discover clusters of arbitrary shape, as it does not rely on the assumption of spherical clusters (as in K-Means). Instead, DBSCAN can group together points that form elongated, irregular, or even disjoint clusters. This makes it particularly effective in applications such as image analysis or geographical data clustering, where clusters often exhibit complex structures. Another significant benefit of DBSCAN is its robustness to noise and outliers. Since points classified as noise are simply ignored in the clustering process, DBSCAN naturally separates noise from the actual clusters, unlike K-Means, which assigns all points to clusters regardless of their suitability.

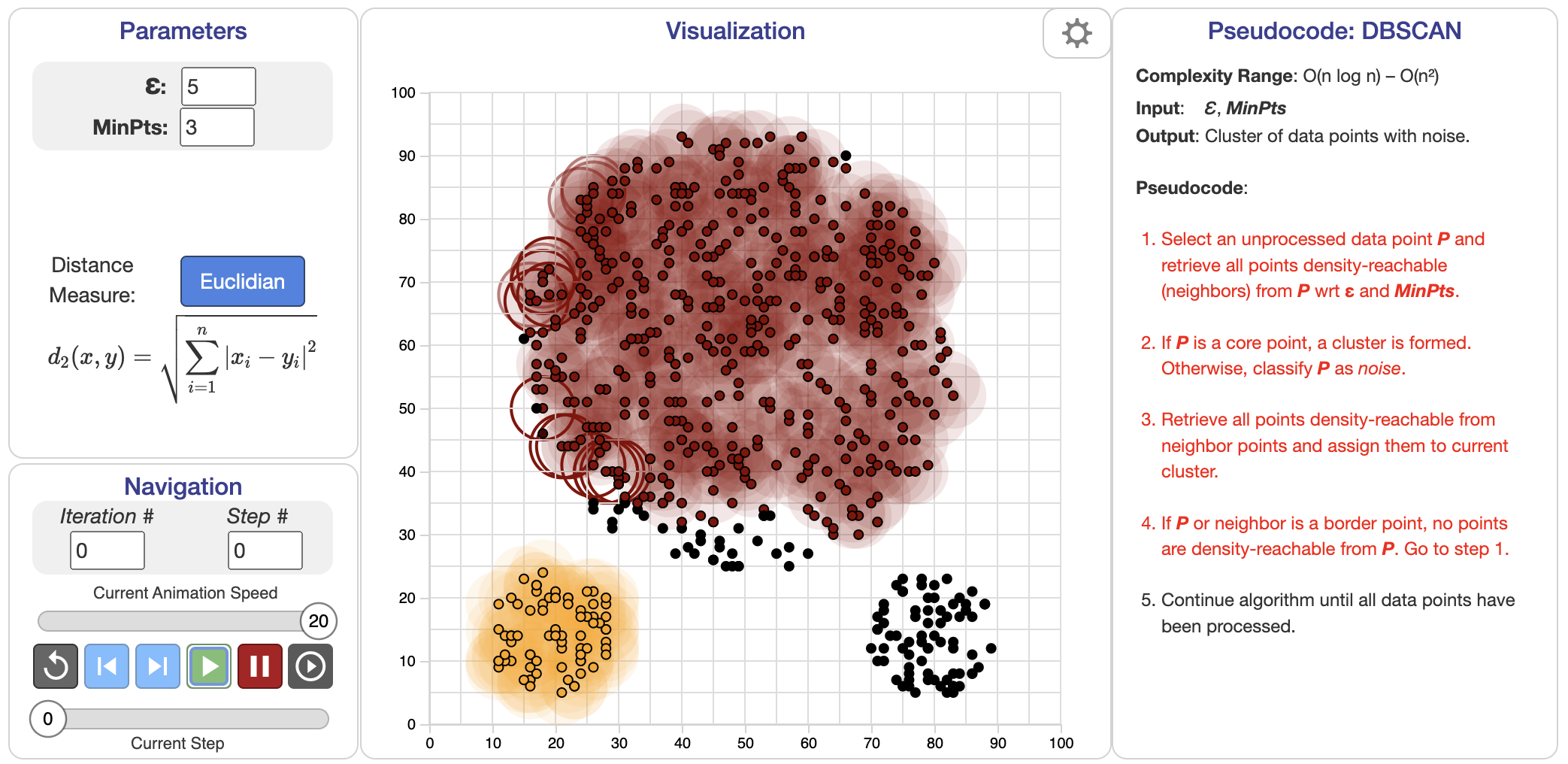
Figure 6: DBSCAN clustering algorithm.

The parameters $\epsilon$ and $\text{minPts}$ are critical to DBSCAN's performance. Choosing an appropriate value for $\epsilon$ can be challenging, as too small a value may cause DBSCAN to classify many points as noise, while too large a value may merge distinct clusters into one. Similarly, $\text{minPts}$ must reflect the underlying density of the dataset. In practice, $\epsilon$ is often determined by examining a k-distance plot, where the distance to the $k$-th nearest neighbor is plotted for each point, and $\epsilon$ is selected at the "elbow" of the plot, representing a sudden increase in distance between points.

Mathematically, the DBSCAN algorithm can be summarized as follows:

• For each point $p \in X$, check if $|N(p)| \geq \text{minPts}$. If true, mark $p$ as a core point.

• For each core point $p$, expand the cluster by recursively adding all points in $N(p)$ that are reachable from $p$.

• Continue until all points are classified as core, border, or noise.

The reachability condition between two points $p$ and $q$ is defined as a chain of core points $p_1, p_2, \dots, p_n$, where $p_1 = p$, $p_n = q$, and $\| p_i - p_{i+1} \| \leq \epsilon$ for all $i$. This allows DBSCAN to capture clusters of arbitrary shapes by connecting regions of high density.

To implement DBSCAN in Rust, we need to create a structure that holds the parameters and the core functionality of the algorithm. Below is a simple implementation that demonstrates how to define a DBSCAN algorithm in Rust:

#[derive(Debug, Clone)]
struct Point {
    x: f64,
    y: f64,
}

struct DBSCAN {
    epsilon: f64,
    min_pts: usize,
}

impl DBSCAN {
    fn new(epsilon: f64, min_pts: usize) -> Self {
        DBSCAN { epsilon, min_pts }
    }

    fn fit(&self, points: &Vec<Point>) -> Vec<Option<usize>> {
        let mut labels = vec![None; points.len()];
        let mut cluster_id = 0;

        for i in 0..points.len() {
            if labels[i].is_none() {
                let neighbors = self.region_query(points, i);
                if neighbors.len() < self.min_pts {
                    labels[i] = Some(0); // Label as noise
                } else {
                    cluster_id += 1;
                    self.expand_cluster(points, &mut labels, i, neighbors, cluster_id);
                }
            }
        }
        labels
    }

    fn region_query(&self, points: &Vec<Point>, index: usize) -> Vec<usize> {
        let mut neighbors = Vec::new();
        for (i, point) in points.iter().enumerate() {
            if self.distance(&points[index], point) <= self.epsilon {
                neighbors.push(i);
            }
        }
        neighbors
    }

    fn distance(&self, p1: &Point, p2: &Point) -> f64 {
        ((p1.x - p2.x).powi(2) + (p1.y - p2.y).powi(2)).sqrt()
    }

    fn expand_cluster(&self, points: &Vec<Point>, labels: &mut Vec<Option<usize>>, point_index: usize, mut neighbors: Vec<usize>, cluster_id: usize) {
        labels[point_index] = Some(cluster_id);

        let mut i = 0;
        while i < neighbors.len() {
            let neighbor_index = neighbors[i];
            if labels[neighbor_index].is_none() {
                labels[neighbor_index] = Some(cluster_id);
                let neighbor_neighbors = self.region_query(points, neighbor_index);
                if neighbor_neighbors.len() >= self.min_pts {
                    neighbors.extend(neighbor_neighbors);
                }
            } else if labels[neighbor_index] == Some(0) {
                labels[neighbor_index] = Some(cluster_id);
            }
            i += 1;
        }
    }
}

fn main() {
    let points = vec![
        Point { x: 1.0, y: 2.0 },
        Point { x: 1.5, y: 1.8 },
        Point { x: 5.0, y: 8.0 },
        Point { x: 8.0, y: 8.0 },
        Point { x: 1.0, y: 0.6 },
        Point { x: 9.0, y: 9.0 },
    ];

    let dbscan = DBSCAN::new(1.5, 2);
    let labels = dbscan.fit(&points);

    for (label, point) in labels.iter().zip(points.iter()) {
        println!("Point: ({}, {}) - Cluster: {:?}", point.x, point.y, label);
    }
}

In this implementation, we create a Point struct to represent the coordinates of each data point. The DBSCAN struct contains the parameters epsilon and min_pts. The fit method processes the points, identifies core points, and expands clusters accordingly. The region_query method finds neighboring points within the defined epsilon radius, while the expand_cluster method marks points as belonging to a cluster and further expands it if necessary.

To tune the parameters epsilon and minPts, one can experiment with different values and evaluate the resulting clusters visually or through cluster validity indices. For instance, using a dataset with known clusters and noise can provide insights into how well DBSCAN performs compared to K-Means and hierarchical clustering.

In practice, the performance of DBSCAN can be compared to K-Means and hierarchical clustering using metrics such as silhouette score or the Davies-Bouldin index. By employing the Rust implementation of DBSCAN, developers can efficiently handle clustering tasks in a type-safe and performant manner, showcasing the capabilities of both Rust and the DBSCAN algorithm in real-world data science applications.

9.5. Gaussian Mixture Models (GMM) link

Gaussian Mixture Models (GMM) represent a powerful probabilistic approach to clustering, which allows us to model the underlying distributions of data points. Unlike simpler clustering techniques, such as K-Means, where each cluster is represented by a centroid, GMMs assume that the data is generated from a mixture of several Gaussian distributions. Each cluster is characterized by its own mean and covariance, which allows GMMs to effectively capture the shapes and orientations of the clusters, especially when they overlap.

The fundamental idea behind GMMs is to view the dataset as a mixture of several Gaussian distributions, where each component of the mixture corresponds to a cluster. This probabilistic modeling enables GMMs to assign soft labels to data points, meaning that instead of assigning each point to a single cluster, GMMs provide a probability distribution over all clusters. This is particularly useful in scenarios where the boundaries between clusters are not well-defined or where clusters exhibit significant overlap.

One of the key methods for estimating the parameters of a Gaussian Mixture Model is the Expectation-Maximization (EM) algorithm. The EM algorithm is an iterative approach that alternates between estimating the expected values of the latent variables (the cluster memberships in the case of GMMs) given the current parameters of the model and then maximizing the likelihood of the data given these expected values to update the model parameters. This process continues until convergence, resulting in the refinement of the Gaussian parameters (means and covariances) that best describe the data.

In the context of GMMs, soft clustering is a significant advantage over hard clustering methods like K-Means. In K-Means, each data point is assigned to one cluster based on the distance to the centroids, leading to hard boundaries. However, GMMs allow for a more nuanced assignment, where each data point has a probability of belonging to each cluster. This feature enables GMMs to accommodate more complex cluster shapes and relationships in the data, making them more flexible and robust for various datasets.

A Gaussian Mixture Model assumes that the data is generated from a mixture of several Gaussian distributions, each representing a cluster. Mathematically, let $X = \{x_1, x_2, \dots, x_n\}$ represent a set of $n$ data points where each $x_i \in \mathbb{R}^d$. The GMM models the probability density function of the data as a weighted sum of $K$ Gaussian components, with each Gaussian having its own mean μk\\mu_kμk and covariance matrix $\Sigma_k$. The mixture model is expressed as:

$$ p(x_i | \Theta) = \sum_{k=1}^{K} \pi_k \mathcal{N}(x_i | \mu_k, \Sigma_k), $$

where $\mathcal{N}(x_i | \mu_k, \Sigma_k)$ represents the multivariate normal distribution for the $k$-th component with mean $\mu_k$ and covariance $\Sigma_k$, and $\pi_k$ is the mixing coefficient for the $k$-th Gaussian component, subject to the constraint $\sum_{k=1}^{K} \pi_k = 1$. The set of parameters $\Theta = \{ \pi_k, \mu_k, \Sigma_k \}$ defines the GMM.

Unlike K-Means, which assigns each point to exactly one cluster, GMM performs soft clustering, meaning that each point belongs to multiple clusters with a certain probability. Specifically, each data point $x_i$ is assigned a responsibility $\gamma(z_{ik})$, which represents the probability that point $x_i$ was generated by the $k$-th Gaussian component. This responsibility is given by:

$$ \gamma(z_{ik}) = \frac{\pi_k \mathcal{N}(x_i | \mu_k, \Sigma_k)}{\sum_{j=1}^{K} \pi_j \mathcal{N}(x_i | \mu_j, \Sigma_j)}. $$

The Expectation-Maximization (EM) algorithm is typically used to estimate the parameters of the GMM. The EM algorithm iteratively refines the parameters $\Theta$ to maximize the likelihood of the observed data under the model. The EM algorithm consists of two steps:

• Expectation (E-step): Compute the responsibilities $\gamma(z_{ik})$ for each data point, based on the current estimates of the parameters.

• Maximization (M-step): Update the parameters $\pi_k$, $\mu_k$, and $\Sigma_k$ based on the responsibilities computed in the E-step. The parameters are updated as follows:

$$ \mu_k^{(t+1)} = \frac{\sum_{i=1}^{n} \gamma(z_{ik}) x_i}{\sum_{i=1}^{n} \gamma(z_{ik})}, $$

$$ \Sigma_k^{(t+1)} = \frac{\sum_{i=1}^{n} \gamma(z_{ik}) (x_i - \mu_k^{(t+1)})(x_i - \mu_k^{(t+1)})^T}{\sum_{i=1}^{n} \gamma(z_{ik})}, $$

$$ \pi_k^{(t+1)} = \frac{1}{n} \sum_{i=1}^{n} \gamma(z_{ik}). $$

These updates are repeated until the likelihood converges, meaning that further iterations produce no significant improvement in the model’s fit to the data.

One of the strengths of GMMs over K-Means is their ability to capture more complex cluster shapes. While K-Means assumes that clusters are spherical and equally sized, GMMs allow clusters to take on elliptical shapes and vary in size due to the flexibility of the covariance matrices. This makes GMMs more suitable for clustering data with overlapping or elongated clusters, where K-Means may fail to correctly separate the clusters.

Additionally, GMMs provide a probabilistic framework for clustering, allowing for uncertainty in the assignment of data points to clusters. In contrast, K-Means enforces hard clustering, assigning each point to exactly one cluster, which can be problematic when clusters overlap. GMMs handle this situation more naturally by assigning probabilities to cluster memberships, thus reflecting the inherent uncertainty in the data.

To implement GMMs in Rust, we can leverage the EM algorithm for parameter estimation. Below is a simplified example that demonstrates how to create a Gaussian Mixture Model from scratch. We will define the necessary structures and functions to fit a GMM to a dataset using the EM algorithm.

First, we will define a structure to represent a Gaussian distribution and a GMM. The Gaussian distribution will hold the mean and covariance, while the GMM will hold the components and their respective weights.

use nalgebra as na;
use na::{DMatrix, DVector};

#[derive(Debug)]
struct Gaussian {
    mean: DVector<f64>,
    covariance: DMatrix<f64>,
}

#[derive(Debug)]
struct GaussianMixtureModel {
    components: Vec<Gaussian>,
    weights: Vec<f64>,
}

impl GaussianMixtureModel {
    fn new(components: Vec<Gaussian>, weights: Vec<f64>) -> Self {
        GaussianMixtureModel { components, weights }
    }

    fn pdf(&self, x: &DVector<f64>) -> f64 {
        self.components
            .iter()
            .enumerate()
            .map(|(i, comp)| {
                let det = comp.covariance.determinant();
                let inv = comp.covariance.clone().try_inverse().unwrap(); // Clone before inversion
                let diff = x - &comp.mean;
                let exponent: f64 = -0.5 * (diff.transpose() * inv * diff.clone())[0]; // Clone diff before reuse
                (1.0 / ((2.0 * std::f64::consts::PI).powi(diff.len() as i32) * det.sqrt())) * exponent.exp() * self.weights[i]
            })
            .sum()
    }
}

In the above code, we define a Gaussian struct that contains the mean and covariance matrix of the distribution. The GaussianMixtureModel struct holds multiple Gaussian components and their weights. The pdf function calculates the probability density function for a given point, summing over all components.

Next, we implement the EM algorithm to fit the GMM to a dataset. The following functions will handle the expectation and maximization steps.

impl GaussianMixtureModel {
    fn expectation(&self, data: &DMatrix<f64>) -> DMatrix<f64> {
        let mut responsibilities = DMatrix::zeros(data.nrows(), self.components.len());
        for (i, x) in data.row_iter().enumerate() {
            let total_pdf = self.pdf(&x.transpose());
            for (j, _) in self.components.iter().enumerate() {
                let comp_pdf = self.pdf(&x.transpose());
                responsibilities[(i, j)] = comp_pdf / total_pdf;
            }
        }
        responsibilities
    }

    fn maximization(&mut self, data: &DMatrix<f64>, responsibilities: &DMatrix<f64>) {
        let n = data.nrows() as f64;
        for (j, comp) in self.components.iter_mut().enumerate() {
            let weight = responsibilities.column(j).sum();
            let weight_normalized = weight / n;

            let mean = (responsibilities.column(j).transpose() * data).transpose() / weight;
            let mut covariance = DMatrix::zeros(data.ncols(), data.ncols());

            for (i, row) in data.row_iter().enumerate() {
                let diff = row.transpose() - &mean;
                covariance += responsibilities[(i, j)] * (diff.clone() * diff.transpose());
            }
            covariance /= weight;

            comp.mean = mean;
            comp.covariance = covariance;
            self.weights[j] = weight_normalized;
        }
    }
}

In the expectation function, we calculate the responsibilities for each data point, which represent the probability that each point belongs to each cluster. In the maximization function, we update the parameters of each Gaussian based on the current responsibilities.

Finally, we can fit the GMM to a dataset and visualize the results. Below is a hypothetical scenario where we use the GMM to cluster a dataset with overlapping clusters and compare the results with K-Means.

fn main() {
    // Create synthetic data with two features
    let data = DMatrix::from_vec(6, 2, vec![
        1.0, 2.0,
        1.5, 1.8,
        5.0, 8.0,
        8.0, 8.0,
        1.0, 0.6,
        9.0, 9.0,
    ]);

    // Initialize GMM with two Gaussian components
    let components = vec![
        Gaussian {
            mean: DVector::from_vec(vec![1.0, 2.0]),
            covariance: DMatrix::identity(2, 2),
        },
        Gaussian {
            mean: DVector::from_vec(vec![8.0, 8.0]),
            covariance: DMatrix::identity(2, 2),
        }
    ];
    let weights = vec![0.5, 0.5]; // Equal weights initially

    let mut gmm = GaussianMixtureModel::new(components, weights);

    // Fit the GMM using Expectation-Maximization (EM)
    for _ in 0..10 {
        let responsibilities = gmm.expectation(&data);
        gmm.maximization(&data, &responsibilities);
    }

    // Display the results
    println!("Fitted Gaussian Mixture Model: {:?}", gmm);
}

In practice, applying GMM to a dataset with overlapping clusters demonstrates its superiority over K-Means in capturing complex cluster structures. GMM assigns probabilities to points, reflecting the uncertainty in overlapping regions, whereas K-Means forces hard assignments, which can result in poor clustering when clusters are not well-separated.

By comparing the results of GMM and K-Means, we observe that GMM provides a more nuanced clustering solution in cases where clusters are elliptical or exhibit overlap. The flexibility of GMMs, combined with the power of the EM algorithm for parameter estimation, makes them a valuable tool for probabilistic clustering in complex datasets.

In conclusion, Gaussian Mixture Models offer a sophisticated and flexible approach to clustering that can effectively handle complex datasets with overlapping clusters. By utilizing the EM algorithm for parameter estimation, GMMs can adapt to the underlying structure of the data, providing soft cluster assignments and capturing intricate relationships. Implementing GMMs in Rust empowers developers to explore advanced machine learning techniques while leveraging the performance and safety features of the Rust programming language.

9.6. Evaluation Metrics for Clustering link

Since clustering is an unsupervised learning problem, there are often no ground truth labels to directly compare the predicted clusters, making evaluation more challenging than in supervised learning. Hence, specialized metrics, such as the silhouette score, Davies-Bouldin index, and adjusted Rand index, have been developed to assess clustering quality.

The fundamental purpose of clustering evaluation is to quantify how well the clustering results capture the underlying structure of the data. This assessment can be performed using internal metrics, which evaluate the clustering based on the data itself without reference to external information, or external metrics, which compare the clustering against a known ground truth when available.

One of the most widely used internal evaluation metrics is the silhouette score, which measures how similar a data point is to its assigned cluster compared to other clusters. Formally, for a data point $x_i$, let $a(x_i)$ represent the average distance between $x_i$ and all other points in the same cluster, and let $b(x_i)$ represent the minimum average distance between $x_i$ and points in any other cluster. The silhouette score for $x_i$ is then given by:

$$ s(x_i) = \frac{b(x_i) - a(x_i)}{\max(a(x_i), b(x_i))}. $$

The silhouette score ranges from -1 to 1, where a value close to 1 indicates that the point is well-clustered, a value close to 0 means the point lies on the boundary between two clusters, and negative values suggest the point may have been misclassified into the wrong cluster. The overall silhouette score for the clustering is the mean silhouette score overall points in the dataset.

Another important internal evaluation metric is the Davies-Bouldin index, which quantifies the average similarity ratio between each cluster and its most similar cluster. The similarity between two clusters is measured by the ratio of within-cluster scatter to the distance between cluster centroids. Mathematically, for each cluster $C_i$, the scatter $S_i$ is defined as the average distance between points in $C_i$ and the centroid $\mu_i$ of that cluster:

$$ S_i = \frac{1}{|C_i|} \sum_{x_j \in C_i} \| x_j - \mu_i \|. $$

The Davies-Bouldin index is computed as:

$$ DB = \frac{1}{K} \sum_{i=1}^{K} \max_{j \neq i} \left( \frac{S_i + S_j}{\| \mu_i - \mu_j \|} \right), $$

where $K$ is the number of clusters, and the term inside the maximum function represents the ratio of within-cluster scatter to between-cluster separation. A lower Davies-Bouldin index indicates better clustering, with more compact clusters that are well-separated from each other.

When ground truth labels are available, external metrics can be used to evaluate clustering performance by comparing the predicted clusters with the true labels. One such external metric is the adjusted Rand index (ARI), which measures the agreement between the clustering and the ground truth while correcting for random chance. The ARI is defined based on pairwise agreements between points, where two points can either belong to the same cluster in both the predicted and true clustering or belong to different clusters in both. The formula for ARI is:

$$ ARI = \frac{\text{Index} - \mathbb{E}[\text{Index}]}{\max(\text{Index}) - \mathbb{E}[\text{Index}]}, $$

where $\text{Index}$ represents the actual count of agreements between clusters, and $\mathbb{E}[\text{Index}]$ represents the expected count of agreements under a random clustering assignment. The ARI ranges from -1 to 1, where 1 indicates perfect agreement between the predicted and true clusters, 0 indicates random clustering, and negative values suggest worse than random clustering.

An important distinction in clustering evaluation is between internal and external metrics. Internal metrics, such as silhouette score and Davies-Bouldin index, evaluate the clustering based on the geometry and distribution of the data itself. These metrics are particularly useful when ground truth labels are unavailable. In contrast, external metrics like the adjusted Rand index are used when true labels are available and can provide a more objective measure of clustering performance by directly comparing the predicted clusters to the known categories.

One challenge in assessing clustering quality, especially in unsupervised learning, is that there is no universally optimal metric for all situations. Each metric has its strengths and weaknesses. For example, the silhouette score performs well when clusters are compact and well-separated, but it may struggle when clusters have irregular shapes. Similarly, the Davies-Bouldin index penalizes clusters with high internal variability but may not be as sensitive to misclassified points near cluster boundaries. Moreover, when there are no ground truth labels, it can be difficult to know which internal metric best reflects the true structure of the data.

To practically implement clustering evaluation metrics in Rust, we need to develop functions that calculate these metrics based on the results of different clustering algorithms. Below is a simple example that demonstrates how to compute the silhouette score and Davies-Bouldin index for clustering results in Rust:

use nalgebra as na;
use na::{DMatrix, DVector};

// Compute pairwise Euclidean distance
fn euclidean_distance(x: &DVector<f64>, y: &DVector<f64>) -> f64 {
    ((x - y).norm_squared()).sqrt()
}

// Compute the silhouette score for clustering
fn silhouette_score(data: &DMatrix<f64>, labels: &Vec<usize>) -> f64 {
    let n = data.nrows();
    let mut total_score = 0.0;

    for i in 0..n {
        let current_label = labels[i];
        let mut a_i = 0.0;
        let mut b_i = f64::MAX;
        let mut cluster_size = 0;

        for j in 0..n {
            if labels[j] == current_label {
                a_i += euclidean_distance(&data.row(i).transpose(), &data.row(j).transpose());
                cluster_size += 1;
            }
        }
        a_i /= cluster_size as f64;

        for k in 0..n {
            if labels[k] != current_label {
                let mut cluster_dist = 0.0;
                let mut other_cluster_size = 0;

                for l in 0..n {
                    if labels[l] == labels[k] {
                        cluster_dist += euclidean_distance(&data.row(i).transpose(), &data.row(l).transpose());
                        other_cluster_size += 1;
                    }
                }
                cluster_dist /= other_cluster_size as f64;
                b_i = b_i.min(cluster_dist);
            }
        }

        total_score += (b_i - a_i) / b_i.max(a_i);
    }

    total_score / n as f64
}

// Compute the Davies-Bouldin index for clustering
fn davies_bouldin_index(data: &DMatrix<f64>, labels: &Vec<usize>) -> f64 {
    let k = labels.iter().cloned().max().unwrap_or(0) + 1;
    let mut cluster_means = Vec::with_capacity(k);
    let mut cluster_sizes = vec![0; k];
    let mut db_index = 0.0;

    for i in 0..k {
        let mut cluster_sum = DVector::zeros(data.ncols());
        for j in 0..data.nrows() {
            if labels[j] == i {
                cluster_sum += data.row(j).transpose();
                cluster_sizes[i] += 1;
            }
        }
        cluster_means.push(cluster_sum / cluster_sizes[i] as f64);
    }

    for i in 0..k {
        let mut s_i = 0.0;
        for j in 0..data.nrows() {
            if labels[j] == i {
                s_i += euclidean_distance(&data.row(j).transpose(), &cluster_means[i]);
            }
        }
        s_i /= cluster_sizes[i] as f64;

        let mut max_r_ij: f64 = 0.0;
        for j in 0..k {
            if i != j {
                let mut s_j = 0.0;
                for l in 0..data.nrows() {
                    if labels[l] == j {
                        s_j += euclidean_distance(&data.row(l).transpose(), &cluster_means[j]);
                    }
                }
                s_j /= cluster_sizes[j] as f64;

                let r_ij = (s_i + s_j) / euclidean_distance(&cluster_means[i], &cluster_means[j]);
                max_r_ij = max_r_ij.max(r_ij);
            }
        }
        db_index += max_r_ij;
    }

    db_index / k as f64
}

fn main() {
    let data = DMatrix::from_row_slice(6, 2, &[
        1.0, 2.0, 
        2.0, 2.0, 
        2.0, 3.0, 
        8.0, 7.0, 
        8.0, 8.0, 
        25.0, 80.0
    ]);

    let labels = vec![0, 0, 0, 1, 1, 2];

    let silhouette = silhouette_score(&data, &labels);
    let db_index = davies_bouldin_index(&data, &labels);

    println!("Silhouette Score: {}", silhouette);
    println!("Davies-Bouldin Index: {}", db_index);
}

In this code, the silhouette_score function calculates the silhouette score by measuring how similar each point is to its own cluster compared to other clusters. The davies_bouldin_index function computes the Davies-Bouldin index, which evaluates the average similarity between each cluster and its most similar cluster. Both functions rely on the euclidean_distance function to compute pairwise distances between data points.

By implementing these evaluation metrics in Rust and applying them to various clustering algorithms, we can assess the quality of clusters and compare the performance of different methods. Analyzing these metrics helps in understanding the strengths and weaknesses of each clustering approach, guiding the selection of the most appropriate algorithm for a given dataset.

In conclusion, evaluating clustering quality is essential for understanding the performance of clustering algorithms, especially in the absence of ground truth labels. The use of internal metrics like the silhouette score and Davies-Bouldin index, along with external metrics like the adjusted Rand index, allows for a comprehensive assessment of clustering results. Implementing these metrics in Rust enables practical experimentation and provides valuable insights into the strengths and limitations of different clustering approaches.

9.7. Conclusion link

Chapter 9 equips you with the knowledge and skills to implement and evaluate clustering algorithms using Rust. Mastering these techniques will enable you to discover hidden patterns and structures in data, providing valuable insights into complex datasets.

9.7.1. Further Learning with GenAI link

These prompts are designed to encourage deep exploration of the theoretical concepts, practical techniques, and implementation strategies related to clustering algorithms in Rust. Each prompt will help you gain a thorough understanding of clustering and its application in various contexts.

• Explain the fundamental principles of clustering. How does clustering differ from classification, and what are the key challenges involved in grouping similar data points without labels? Implement a simple clustering algorithm in Rust and apply it to a small dataset.

• Discuss the K-Means algorithm. How does K-Means partition data into clusters, and what are the challenges related to choosing the number of clusters (K)? Implement K-Means in Rust and experiment with different values of K on a real-world dataset.

• Analyze the convergence behavior of the K-Means algorithm. How does the choice of initial centroids affect the algorithm's performance, and what strategies can be used to improve initialization? Implement K-Means in Rust with different initialization methods and compare the results.

• Explore the concept of hierarchical clustering. How does hierarchical clustering build a dendrogram, and what are the differences between agglomerative and divisive approaches? Implement agglomerative hierarchical clustering in Rust and visualize the dendrogram.

• Discuss the different linkage criteria used in hierarchical clustering. How do single, complete, and average linkage affect the clustering results, and what are the trade-offs between them? Implement different linkage criteria in Rust and compare their effects on a dataset.

• Analyze the strengths and limitations of DBSCAN. How does DBSCAN identify clusters based on density, and how does it handle noise and outliers? Implement DBSCAN in Rust and apply it to a dataset with noise to evaluate its performance.

• Explore the role of the epsilon and minPts parameters in DBSCAN. How do these parameters influence the clustering results, and what strategies can be used to tune them effectively? Implement DBSCAN in Rust with different parameter settings and analyze the impact on clustering quality.

• Discuss the Gaussian Mixture Models (GMM) approach to clustering. How do GMMs represent clusters as mixtures of Gaussian distributions, and what are the advantages of using GMMs over K-Means? Implement GMMs in Rust using the Expectation-Maximization algorithm and apply them to a complex dataset.

• Analyze the Expectation-Maximization (EM) algorithm used in GMMs. How does the EM algorithm iteratively estimate the parameters of the Gaussian distributions, and what challenges might arise during its implementation? Implement the EM algorithm in Rust for GMMs and apply it to a dataset with overlapping clusters.

• Explore the concept of soft clustering in GMMs. How does GMM perform soft clustering by assigning probabilities to data points belonging to different clusters, and what benefits does this approach offer? Implement soft clustering in Rust using GMMs and compare it with hard clustering methods like K-Means.

• Discuss the importance of evaluating clustering results. What are the key challenges in clustering evaluation, and how do internal and external metrics help assess clustering quality? Implement clustering evaluation metrics in Rust and apply them to results from different algorithms.

• Analyze the silhouette score as a clustering evaluation metric. How does the silhouette score measure the cohesion and separation of clusters, and what are its limitations? Implement the silhouette score in Rust and use it to evaluate the quality of K-Means and DBSCAN clusters.

• Explore the Davies-Bouldin index as a clustering evaluation metric. How does the Davies-Bouldin index assess clustering quality based on the average similarity ratio of each cluster, and when is it most useful? Implement the Davies-Bouldin index in Rust and compare its results with other evaluation metrics.

• Discuss the adjusted Rand index as an external clustering evaluation metric. How does the adjusted Rand index compare the similarity between the predicted and true clusterings, and what are its strengths in assessing clustering performance? Implement the adjusted Rand index in Rust and apply it to a labeled dataset.

• Analyze the trade-offs between different clustering algorithms. In what scenarios might K-Means be preferred over DBSCAN or GMMs, and how can these algorithms be combined for improved performance? Implement a comparative analysis of clustering algorithms in Rust using a real-world dataset.

• Explore the impact of feature scaling on clustering algorithms. How does feature scaling affect the performance and results of clustering methods like K-Means and DBSCAN, and what are the best practices for scaling data? Implement feature scaling in Rust and analyze its effect on clustering results.

• Discuss the challenges of clustering high-dimensional data. How do issues like the curse of dimensionality affect clustering performance, and what techniques can be used to mitigate these challenges? Implement dimensionality reduction techniques in Rust before applying clustering algorithms to high-dimensional data.

• Analyze the application of clustering algorithms to time-series data. What unique challenges does time-series data present for clustering, and how can algorithms like K-Means and DBSCAN be adapted for this purpose? Implement clustering for time-series data in Rust and evaluate the results.

• Explore the role of anomaly detection in clustering. How can clustering algorithms like DBSCAN be used to identify anomalies or outliers in data, and what are the key considerations for implementing this approach? Implement anomaly detection using clustering in Rust and apply it to a real-world dataset.

• Discuss the use of clustering in customer segmentation. How can clustering algorithms be applied to segment customers based on their behavior, and what are the benefits of this approach in marketing and business analysis? Implement a customer segmentation model in Rust using clustering and analyze the results.

Each prompt challenges you to explore, experiment, and critically analyze different approaches, helping you become a more proficient and innovative machine learning practitioner. Embrace these challenges as opportunities to expand your expertise and apply clustering techniques to uncover hidden patterns and structures in complex datasets.

9.7.2. Hands On Practices link

These exercises are designed to be challenging and in-depth, requiring you to apply both theoretical knowledge and practical skills in Rust.