13.1. Introduction to Probabilistic Graphical Models link

Probabilistic Graphical Models (PGMs) offer a robust framework for handling complex systems involving multiple interdependent random variables, which often appear in domains characterized by uncertainty and incomplete information. PGMs encode the joint distribution of these variables in a graphical form, facilitating not only the modeling of such systems but also reasoning and inference over them. Formally, a PGM consists of a set of random variables $X_1, X_2, \dots, X_n$ represented by nodes, and edges between the nodes that capture the probabilistic dependencies among these variables. The edges provide a graphical means to express conditional independence, which is crucial for simplifying joint distributions into manageable components.

Mathematically, the joint probability distribution of a set of random variables $X_1, X_2, \dots, X_n$ can be denoted as $P(X_1, X_2, \dots, X_n)$. In the absence of any structure, the full joint distribution may involve a large number of terms, making direct computation infeasible, especially when the number of variables is large. However, PGMs exploit the concept of conditional independence to break down the joint distribution into smaller, manageable factors. Conditional independence states that two random variables $X_i$ and $X_j$ are conditionally independent given a set of variables $Y$ if $P(Xj∣Y)P(X_i, X_j \mid Y) = P(X_i \mid Y) P(X_j \mid Y)$. This relationship allows us to simplify the joint distribution by factoring it according to the dependencies encoded in the graph.

There are two primary types of PGMs: directed graphical models, also known as Bayesian Networks, and undirected graphical models, known as Markov Networks. In a Bayesian Network, the nodes represent random variables, and the directed edges represent conditional dependencies between these variables. The joint distribution of the variables in a Bayesian Network can be factored as a product of conditional probabilities. Formally, if $X_1, X_2, \dots, X_n$ are random variables in a Bayesian Network, the joint probability distribution is given by:

$$ P(X_1, X_2, \dots, X_n) = \prod_{i=1}^{n} P(X_i \mid \text{Pa}(X_i)), $$

where $\text{Pa}(X_i)$ denotes the set of parent nodes of $X_i$. This factorization expresses the joint distribution in terms of local conditional probabilities, leveraging the conditional independence assumptions inherent in the graph structure.

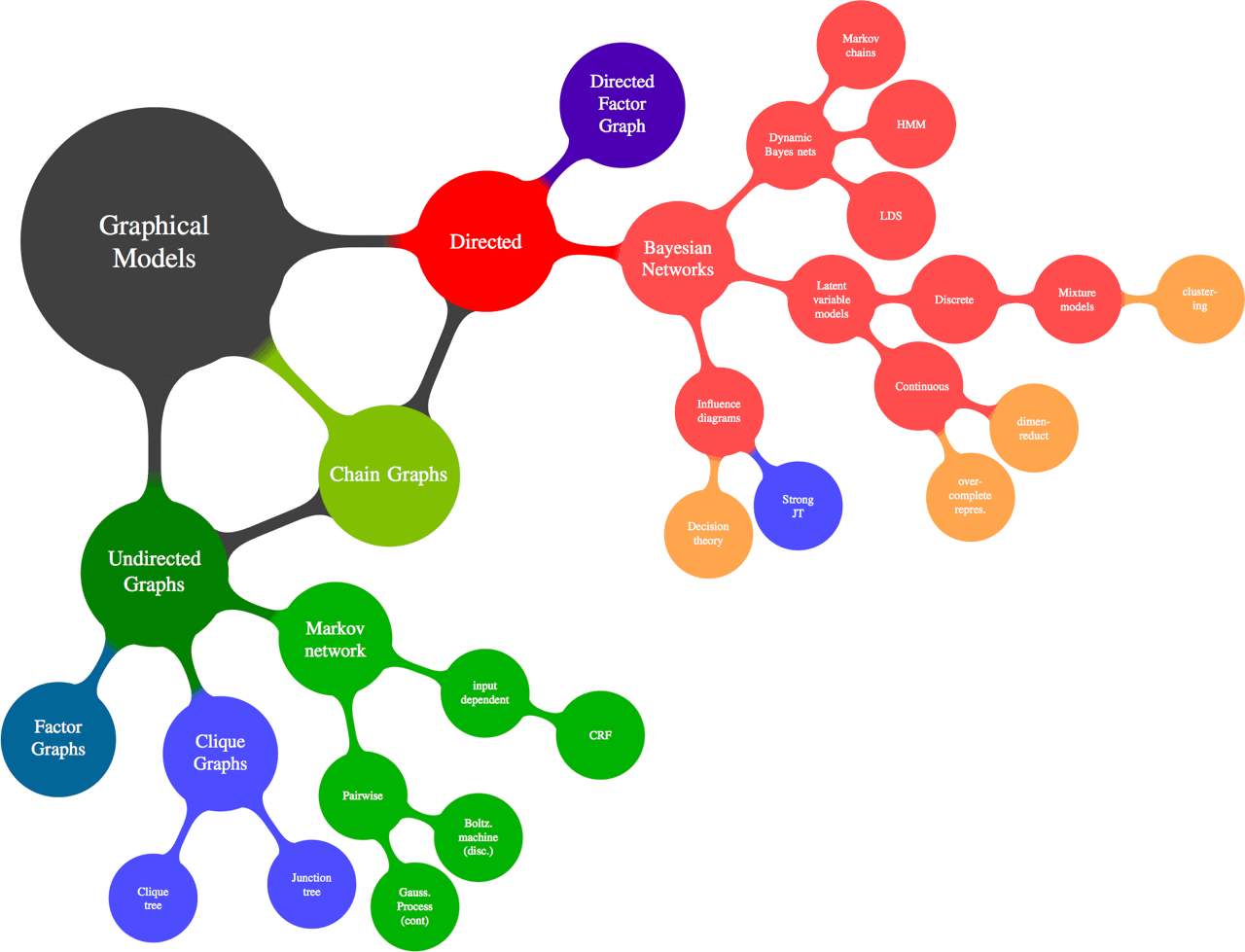
Figure 1: Types of graphs - mainly directed and undirected.

In contrast, Markov Networks use undirected edges to represent relationships between variables. These networks are particularly useful in situations where the directionality of the dependencies is not well-defined or is symmetric. The joint distribution in a Markov Network can be represented as a product of potential functions defined over the cliques of the graph. If $X_1, X_2, \dots, X_n$ are random variables in a Markov Network, the joint distribution can be written as:

$$ P(X_1, X_2, \dots, X_n) = \frac{1}{Z} \prod_{C \in \mathcal{C}} \phi_C(X_C), $$

where $\mathcal{C}$ denotes the set of cliques in the graph, $\phi_C(X_C)$ is the potential function defined over the clique $C$, and $Z$ is the normalization constant known as the partition function. Unlike Bayesian Networks, Markov Networks do not imply any specific direction of influence between variables, which makes them suitable for modeling undirected relationships.

Both types of PGMs rely on the concept of conditional independence to simplify complex joint distributions. The graphical structure allows us to infer relationships between variables, compute marginal probabilities efficiently, and update beliefs in light of new evidence through algorithms such as belief propagation in Bayesian Networks or the junction tree algorithm in Markov Networks.

In summary, PGMs provide a mathematically rigorous and conceptually elegant way to represent and reason about systems with uncertain variables. By leveraging conditional independence and exploiting the structure of the graph, they enable efficient computation, making them indispensable tools in fields ranging from machine learning to statistics and artificial intelligence. The formalism of PGMs, whether in the form of Bayesian Networks or Markov Networks, allows us to decompose complex systems into smaller, more manageable components, facilitating both theoretical analysis and practical implementation.

In practical terms, implementing a simple PGM in Rust involves creating a representation of a graphical model that captures the dependencies between variables. Let’s consider a basic example: a PGM with two variables, $A$ and $B$, where $A$ influences $B$. To start, you would define a graph structure that includes nodes for each variable and directed edges to represent the influence of $A$ on $B$. Here's a basic Rust implementation using a graph library to create and visualize this model:

use petgraph::graph::DiGraph;

fn main() {
    // Create a directed graph
    let mut graph = DiGraph::new();

    // Add nodes representing variables A and B
    let a = graph.add_node("A");
    let b = graph.add_node("B");

    // Add an edge from A to B, representing A influencing B
    graph.add_edge(a, b, ());

    // Print the nodes and edges
    for node in graph.node_indices() {
        println!("Node: {:?}", graph[node]);
    }
    for edge in graph.edge_indices() {
        let (source, target) = graph.edge_endpoints(edge).unwrap();
        println!("Edge from {:?} to {:?}", graph[source], graph[target]);
    }
}

In this example, we use the petgraph library to create a directed graph. We add two nodes, A and B, and an edge from A to B to represent the influence of A on B. The printed output shows the nodes and edges of the graph, allowing us to understand how the graph encodes the dependencies between variables.

Visualizing the graph can further enhance our understanding of the PGM. Tools and libraries for graph visualization can be used to create diagrams that illustrate the structure of the PGM, making it easier to see how dependencies are represented and to validate the correctness of the model.

In summary, Probabilistic Graphical Models are instrumental in simplifying the representation of complex probabilistic relationships. By leveraging graphical structures, PGMs provide a clear and manageable way to understand and compute joint distributions, conditional independencies, and dependencies between random variables. The practical implementation in Rust, as demonstrated, offers a foundational approach to building and visualizing these models.

13.2. Directed Graphical Models: Bayesian Networks link

Bayesian Networks are a form of probabilistic graphical models that represent conditional dependencies among a set of random variables using a directed acyclic graph (DAG). Each node in the network corresponds to a random variable, while the directed edges between nodes represent probabilistic dependencies. The acyclic nature of the graph guarantees the absence of feedback loops or cycles, ensuring that any sequence of dependencies between variables terminates, which significantly simplifies both inference and computation of joint probabilities.

Mathematically, let $X_1, X_2, \dots, X_n$ represent the random variables in a Bayesian Network. The joint probability distribution over these variables can be expressed as a product of conditional probabilities. Specifically, if $\text{Pa}(X_i)$ denotes the set of parent nodes of the variable $X_i$, the joint probability distribution is given by:

$$ P(X_1, X_2, \dots, X_n) = \prod_{i=1}^{n} P(X_i \mid \text{Pa}(X_i)), $$

where $P(X_i \mid \text{Pa}(X_i))$ represents the conditional probability of $X_i$ given its parent variables in the graph. This factorization is one of the key strengths of Bayesian Networks, as it allows us to decompose a potentially intractable joint distribution into a set of smaller, more manageable conditional distributions. This decomposition exploits the conditional independence properties encoded by the DAG structure, which dramatically reduces the complexity of representing and computing probabilities in high-dimensional systems.

A crucial concept in Bayesian Networks is d-separation, which provides a formal criterion for determining whether two sets of variables are conditionally independent, given a third set. If a set of nodes $X$ is d-separated from another set $Y$ by a third set Z, then $X$ and $Y$ are conditionally independent given $Z$, denoted as $X \perp Y \mid Z$. D-separation relies on analyzing the paths between nodes in the DAG and understanding how information can or cannot flow through the network based on the structure. It is a powerful tool for simplifying the computation of joint distributions and for making inferences about the relationships between variables.

Performing inference in Bayesian Networks typically involves computing the posterior distribution of certain variables given observed values for other variables. For example, given a set of observed variables $X_{\text{obs}}$, the goal is to compute $P(X_{\text{query}} \mid X_{\text{obs}})$, where $X_{\text{query}}$represents the set of variables of interest. In practice, exact inference in Bayesian Networks can be computationally expensive, especially in large networks, but algorithms such as belief propagation (also known as message passing) are often used to efficiently compute these posterior probabilities. Belief propagation works by sending "messages" between nodes in the graph, propagating information about the probabilities through the network based on local conditional distributions. When the network is tree-structured (i.e., when the graph has no loops), belief propagation is guaranteed to compute exact probabilities efficiently. In more general networks, approximate inference methods such as loopy belief propagation may be employed.

Bayesian Networks are particularly useful for reasoning about uncertainty and causal relationships in complex systems. Because the directed edges of the DAG represent causal dependencies, Bayesian Networks can be used to model not only the probabilistic relationships between variables but also the underlying causal structure of the system. For instance, if an edge exists from node $X$ to node $Y$, this implies that $X$ directly influences $Y$, and the strength of this influence is quantified by the conditional probability $P(Y \mid X)$.

Furthermore, the use of Bayesian inference allows for the updating of beliefs in the light of new evidence. When observations become available, the posterior distribution can be computed by conditioning the joint distribution on the observed values, allowing for dynamic reasoning as more data is gathered. This is particularly valuable in fields such as medical diagnosis, where Bayesian Networks can be used to infer the likelihood of various diseases given symptoms and test results, or in robotics, where they can help in decision-making under uncertainty.

In summary, Bayesian Networks offer a mathematically grounded framework for modeling and reasoning about complex systems governed by probabilistic and causal relationships. The ability to factorize the joint distribution into local conditional probabilities, combined with the powerful concept of d-separation, makes them an essential tool for efficient inference. By leveraging algorithms such as belief propagation, Bayesian Networks can handle large-scale problems in a computationally tractable manner, while also providing a clear interpretation of the dependencies and causal structure within the system.

To illustrate how to implement a Bayesian Network in Rust, let’s consider a simple example where we have a network with three variables: A, B, and C. Variable A influences both B and C, but B and C are conditionally independent given A. We will construct the network, calculate joint probabilities, and perform inference using Rust.

First, we need to define the network structure and the conditional probability tables (CPTs). We can use a basic Rust implementation for this purpose:

use std::collections::HashMap;

#[derive(Debug)]
struct BayesianNetwork {
    cpt: HashMap<(String, String), f64>, // Conditional Probability Table
}

impl BayesianNetwork {
    fn new() -> Self {
        BayesianNetwork {
            cpt: HashMap::new(),
        }
    }

    fn set_cpt(&mut self, variable: &str, given: &str, probability: f64) {
        self.cpt.insert((variable.to_string(), given.to_string()), probability);
    }

    fn get_probability(&self, variable: &str, given: &str) -> f64 {
        *self.cpt.get(&(variable.to_string(), given.to_string())).unwrap_or(&0.0)
    }

    fn joint_probability(&self, a: bool, b: bool, c: bool) -> f64 {
        let p_a = if a { 0.7 } else { 0.3 }; // P(A)
        let p_b_given_a = if a { self.get_probability("B", if b { "true" } else { "false" }) } else { 1.0 };
        let p_c_given_a = if a { self.get_probability("C", if c { "true" } else { "false" }) } else { 1.0 };

        p_a * p_b_given_a * p_c_given_a
    }
}

fn main() {
    let mut bn = BayesianNetwork::new();

    // Define CPTs for the network
    bn.set_cpt("B", "true", 0.8);
    bn.set_cpt("C", "true", 0.9);

    // Calculate joint probability P(A=true, B=true, C=true)
    let prob = bn.joint_probability(true, true, true);
    println!("Joint Probability P(A=true, B=true, C=true): {}", prob);
}

In this example, we create a BayesianNetwork struct with a conditional probability table (CPT) to store the probabilities. The set_cpt method allows us to define the conditional probabilities, while the get_probability method retrieves them. The joint_probability method calculates the joint probability of variables A, B, and C based on the conditional probabilities. For simplicity, fixed probabilities are used, but in a real-world scenario, these would be derived from data or specified more precisely.

To perform inference, such as calculating the marginal probability of B given that A is true, you would need to sum over the joint probabilities for all possible values of the remaining variables:

use std::collections::HashMap;

#[derive(Debug)]
struct BayesianNetwork {
    cpt: HashMap<(String, String), f64>, // Conditional Probability Table
}

impl BayesianNetwork {
    fn new() -> Self {
        BayesianNetwork {
            cpt: HashMap::new(),
        }
    }

    fn set_cpt(&mut self, variable: &str, given: &str, probability: f64) {
        self.cpt.insert((variable.to_string(), given.to_string()), probability);
    }

    fn get_probability(&self, variable: &str, given: &str) -> f64 {
        *self.cpt.get(&(variable.to_string(), given.to_string())).unwrap_or(&0.0)
    }

    fn joint_probability(&self, a: bool, b: bool, c: bool) -> f64 {
        let p_a = if a { 0.7 } else { 0.3 }; // P(A)
        let p_b_given_a = if a { self.get_probability("B", if b { "true" } else { "false" }) } else { 1.0 };
        let p_c_given_a = if a { self.get_probability("C", if c { "true" } else { "false" }) } else { 1.0 };

        p_a * p_b_given_a * p_c_given_a
    }
}

fn marginal_probability_given_a(b: bool, bn: &BayesianNetwork) -> f64 {
    let p_a_true = 0.7;
    let p_b_given_a_true = bn.get_probability("B", if b { "true" } else { "false" });

    p_a_true * p_b_given_a_true
}

fn main() {
    let mut bn = BayesianNetwork::new();

    // Define CPTs for the network
    bn.set_cpt("B", "true", 0.8);
    bn.set_cpt("C", "true", 0.9);

    // Calculate joint probability P(A=true, B=true, C=true)
    let prob_joint = bn.joint_probability(true, true, true);
    println!("Joint Probability P(A=true, B=true, C=true): {}", prob_joint);

    // Calculate marginal probability P(B=true | A=true)
    bn.set_cpt("B", "A", 0.8); // Set CPT for B given A
    let prob_b_given_a = marginal_probability_given_a(true, &bn);
    println!("Marginal Probability P(B=true | A=true): {}", prob_b_given_a);
}

In this code snippet, marginal_probability_given_a calculates the marginal probability of B given that A is true by summing over the joint probabilities. This example illustrates the basic approach to Bayesian Network implementation and inference in Rust.

Overall, Bayesian Networks provide a robust framework for modeling and reasoning about probabilistic systems. By representing conditional dependencies through a directed acyclic graph, these models facilitate the factorization of joint probability distributions and enable efficient inference. Implementing and working with Bayesian Networks in Rust involves constructing the network, defining CPTs, calculating joint probabilities, and performing inference, as demonstrated in the provided examples.

13.3. Undirected Graphical Models: Markov Networks link

Markov Networks, also referred to as Markov Random Fields (MRFs), are a class of probabilistic graphical models that represent dependencies between random variables using undirected graphs. In a Markov Network, the nodes represent random variables, and the edges between these nodes indicate conditional dependencies. Unlike Bayesian Networks, which rely on directed edges to encode causal relationships, Markov Networks use undirected edges to model symmetric relationships between variables. This undirected structure implies that the variables connected by an edge are conditionally dependent, and any variable is conditionally independent of all other variables in the network given its neighbors, a property known as the Markov property.

Formally, let $X_1, X_2, \dots, X_n$ represent the random variables in the Markov Network. The key assumption is that for any random variable $X_i$, its conditional probability distribution depends only on its neighbors in the graph. More precisely, $X_i$ is conditionally independent of all other variables in the network given the values of its neighboring variables. Mathematically, this can be expressed as:

$$ P(X_i \mid X_{\text{all} \setminus \{i\}}) = P(X_i \mid X_{\text{neighbors}(i)}), $$

where $X_{\text{all} \setminus \{i\}}$ represents all variables except $X_i$, and $X_{\text{neighbors}(i)}$ represents the neighboring variables of $X_i$ in the graph.

The joint probability distribution of all the variables in a Markov Network is represented as a product of potential functions, each associated with a clique in the graph. A clique is a subset of nodes in the graph where every pair of nodes is connected by an edge. If $\mathcal{C}$ denotes the set of cliques in the graph, and $\phi_C(X_C)$ represents the potential function over the variables $X_C$ in clique $C$, then the joint probability distribution can be written as:

$$ P(X_1, X_2, \dots, X_n) = \frac{1}{Z} \prod_{C \in \mathcal{C}} \phi_C(X_C), $$

where $Z$ is a normalization constant known as the partition function, ensuring that the distribution sums to 1. The potential functions $\phi_C(X_C)$ are non-negative functions that represent the relative compatibility of different assignments of values to the variables in clique $C$, but they do not necessarily have a probabilistic interpretation on their own. The product of these potential functions across all cliques provides a factorized representation of the joint distribution, which simplifies both the representation and computation of probabilities in the network.

A fundamental result in the theory of Markov Networks is the Hammersley-Clifford theorem, which establishes a connection between the graph structure and the factorization of the joint probability distribution. The Hammersley-Clifford theorem states that if a distribution satisfies the Markov properties with respect to an undirected graph, then the joint probability distribution can be factorized into a product of potential functions defined over the cliques of the graph, as shown in the equation above. This theorem provides the theoretical foundation for using cliques to decompose the joint distribution, allowing efficient computation and inference in Markov Networks.

One key difference between Markov Networks and Bayesian Networks is that Markov Networks do not impose any directional dependencies between variables. In a Bayesian Network, the directed edges imply causality, meaning that one variable directly influences another. In contrast, the undirected edges in a Markov Network imply that the relationship between variables is symmetric; the variables influence each other equally, without implying a specific direction of influence. This symmetry makes Markov Networks particularly well-suited for modeling systems where the relationships between variables are bidirectional or where the direction of influence is not clearly defined.

The factorization of the joint distribution into potential functions over cliques also has important computational implications. In practice, the size of the cliques determines the complexity of inference in the network. Larger cliques lead to more complex potential functions, which can make exact inference computationally expensive. For this reason, many algorithms for inference in Markov Networks focus on approximate methods, such as Gibbs sampling or mean field approximation, which allow for tractable computation even in networks with large cliques.

In conclusion, Markov Networks provide a mathematically rigorous framework for modeling probabilistic dependencies in systems with symmetric relationships. The use of undirected graphs allows for a natural representation of systems where variables mutually influence each other, and the factorization of the joint distribution into potential functions over cliques enables efficient computation. The Hammersley-Clifford theorem provides the theoretical underpinning for this factorization, establishing that the joint distribution can always be expressed as a product of clique potentials. By leveraging these mathematical properties, Markov Networks have become a powerful tool for reasoning about complex probabilistic systems in fields ranging from machine learning to statistical physics.

To implement a Markov Network in Rust, let's consider a simple example with three variables: X, Y, and Z, where X and Y are connected, and Y and Z are connected, forming a linear chain. We will construct the network, define potential functions for the cliques, and perform inference using Gibbs sampling.

First, we'll define the network structure and the potential functions:

use std::collections::HashMap;
use std::collections::BTreeSet;

#[derive(Debug)]
struct MarkovNetwork {
    potential_functions: HashMap<BTreeSet<String>, f64>, // Potential functions over cliques
}

impl MarkovNetwork {
    fn new() -> Self {
        MarkovNetwork {
            potential_functions: HashMap::new(),
        }
    }

    fn set_potential_function(&mut self, clique: Vec<String>, potential: f64) {
        let sorted_clique: BTreeSet<String> = clique.into_iter().collect();
        self.potential_functions.insert(sorted_clique, potential);
    }

    fn get_potential_function(&self, clique: &Vec<String>) -> f64 {
        let sorted_clique: BTreeSet<String> = clique.iter().cloned().collect();
        *self.potential_functions.get(&sorted_clique).unwrap_or(&1.0)
    }
}

fn main() {
    let mut mn = MarkovNetwork::new();

    // Define potential functions for the cliques
    mn.set_potential_function(vec!["X".to_string(), "Y".to_string()], 0.8);
    mn.set_potential_function(vec!["Y".to_string(), "Z".to_string()], 0.9);

    // Print the potential functions
    for (clique, potential) in mn.potential_functions.iter() {
        println!("Clique: {:?}, Potential: {}", clique, potential);
    }

    // Demonstrate the usage of get_potential_function
    let clique = vec!["X".to_string(), "Y".to_string()];
    let potential = mn.get_potential_function(&clique);
    println!("Potential function for clique {:?}: {}", clique, potential);
}

In this code, the MarkovNetwork struct holds potential functions for different cliques of the network. The set_potential_function method allows us to define potential functions, and the get_potential_function method retrieves them. We then print the potential functions for the cliques in the network.

To perform inference using Gibbs sampling, we need to sample from the distribution defined by the potential functions. Gibbs sampling involves iteratively sampling each variable while fixing the values of others. Here’s a simplified implementation of Gibbs sampling:

use std::collections::HashMap;
use std::collections::BTreeSet;
use rand::Rng;

#[derive(Debug)]
struct MarkovNetwork {
    potential_functions: HashMap<BTreeSet<String>, f64>, // Potential functions over cliques
}

impl MarkovNetwork {
    fn new() -> Self {
        MarkovNetwork {
            potential_functions: HashMap::new(),
        }
    }

    fn set_potential_function(&mut self, clique: Vec<String>, potential: f64) {
        let sorted_clique: BTreeSet<String> = clique.into_iter().collect();
        self.potential_functions.insert(sorted_clique, potential);
    }
}

fn gibbs_sampling(num_samples: usize) -> Vec<HashMap<String, bool>> {
    let mut rng = rand::thread_rng();
    let mut samples = Vec::new();

    for _ in 0..num_samples {
        let mut sample = HashMap::new();
        let x = rng.gen_bool(0.5);
        let y = rng.gen_bool(0.5);
        let z = rng.gen_bool(0.5);

        sample.insert("X".to_string(), x);
        sample.insert("Y".to_string(), y);
        sample.insert("Z".to_string(), z);

        samples.push(sample);
    }

    samples
}

fn main() {
    let mut mn = MarkovNetwork::new();
    // Define potential functions for the cliques
    mn.set_potential_function(vec!["X".to_string(), "Y".to_string()], 0.8);
    mn.set_potential_function(vec!["Y".to_string(), "Z".to_string()], 0.9);

    let samples = gibbs_sampling(100);

    // Print a few samples
    for sample in samples.iter().take(5) {
        println!("{:?}", sample);
    }
}

In this example, gibbs_sampling generates samples from the Markov Network by randomly assigning values to each variable. This is a basic implementation and does not consider the potential functions or perform true Gibbs sampling, but it illustrates the sampling concept.

Overall, Markov Networks offer a flexible framework for modeling dependencies between variables using undirected graphs. By representing joint distributions through potential functions over cliques and utilizing techniques like Gibbs sampling, these models provide a powerful tool for probabilistic reasoning and inference. The Rust implementation examples demonstrate the construction of a Markov Network, defining potential functions, and performing basic sampling, laying the foundation for more advanced probabilistic modeling and inference.

13.4. Exact Inference in Graphical Models link

Exact inference methods are crucial in probabilistic graphical models for determining precise probabilities, marginal distributions, and conditional probabilities. These methods are foundational for performing rigorous probabilistic reasoning in models where exact solutions are computationally feasible. Among the most widely used techniques for exact inference are variable elimination, belief propagation, and the junction tree algorithm. Each method provides a systematic approach for navigating the complexity of graphical models, allowing for the computation of various probabilistic measures with precision, though often at significant computational cost.

Variable elimination is a classic technique used for computing marginal probabilities. The goal of this method is to marginalize, or eliminate, variables from the joint probability distribution one at a time, reducing the overall complexity of the problem step by step. Consider a set of random variables $X_1, X_2, \dots, X_n$ with a joint probability distribution $P(X_1, X_2, \dots, X_n)$. To compute the marginal probability of a subset of variables, say $P(X_1)$, variable elimination systematically sums out the other variables, such as:

$$ P(X_1) = \sum_{X_2, \dots, X_n} P(X_1, X_2, \dots, X_n). $$

This process relies on the factorization properties of probabilistic graphical models. When performing variable elimination, the joint distribution is often expressed as a product of factors corresponding to the local conditional dependencies in the graph. The algorithm then eliminates variables by summing over these factors in an efficient order. However, the computational complexity of this method can grow exponentially with the number of variables, particularly if the graphical model contains large cliques or dense connections. This growth is a direct consequence of the need to maintain intermediate factors, which can become increasingly large as more variables are eliminated. Therefore, while variable elimination is exact, it can become computationally prohibitive for large-scale models.

Belief propagation, also known as message passing, is another key method for performing exact inference in probabilistic graphical models, particularly in tree-structured graphs. In belief propagation, messages are passed between nodes in the graph to update the beliefs, or marginal probabilities, of the variables at each node. Let $X_1, X_2, \dots, X_n$ be the random variables in a tree-structured graph. For each node $X_i$, messages are passed along the edges to neighboring nodes. These messages are functions of the incoming messages from other neighboring nodes, and they encapsulate the local conditional distributions. The marginal distribution for any node $X_i$ is then computed by combining these incoming messages:

$$ P(X_i) \propto \prod_{\text{neighbors}(i)} m_{\text{neighbor} \rightarrow i}(X_i), $$

where $m_{\text{neighbor} \rightarrow i}(X_i)$ represents the message sent from a neighboring node to $X_i$. In tree-structured graphs, belief propagation guarantees exact results by systematically propagating information throughout the graph. However, in graphs with cycles, belief propagation often only provides approximate solutions, as the messages may cycle indefinitely without convergence. For tree-structured graphs, this method is highly efficient and provides exact inference, but its application to general graphs is less reliable for exact results.

The junction tree algorithm extends belief propagation to more complex, non-tree-structured graphs. The fundamental idea behind the junction tree algorithm is to transform the original graph into a tree-like structure, called a junction tree, where each node represents a clique from the original graph. A clique in this context is a fully connected subset of nodes. The junction tree is constructed by clustering the variables into cliques, ensuring that the graph satisfies the running intersection property. The joint probability distribution is then factorized into clique potentials, and exact inference is performed by passing messages between the cliques, similar to belief propagation. If $\mathcal{C}_1, \mathcal{C}_2, \dots, \mathcal{C}_m$ represent the cliques in the junction tree, the joint distribution is represented as:

$$ P(X_1, X_2, \dots, X_n) = \prod_{i=1}^{m} \phi_{\mathcal{C}_i}(X_{\mathcal{C}_i}), $$

where $\phi_{\mathcal{C}_i}(X_{\mathcal{C}_i})$ is the potential function for clique $\mathcal{C}_i$. Inference is then performed by passing messages between cliques, updating the marginal probabilities of the variables in each clique. The junction tree algorithm is particularly powerful for handling complex dependencies in large models, but its computational complexity depends on the size of the cliques in the tree. If the original graph has large cliques, the junction tree may also have large cliques, leading to computational difficulties similar to those in variable elimination.

The computational complexity of these exact inference methods is an important consideration, as it often grows exponentially with the size and density of the graph. In variable elimination, the size of the intermediate factors can grow exponentially with the number of variables being marginalized, especially if the graph contains dense connections. Similarly, in the junction tree algorithm, the size of the cliques in the junction tree determines the computational burden. For large and complex graphs, the number of possible configurations of the variables grows exponentially, leading to a combinatorial explosion in the number of computations required. This makes exact inference methods impractical for very large models. Consequently, while exact inference methods provide highly accurate results, they are often traded off against efficiency in favor of approximate methods when dealing with real-world problems that involve large-scale probabilistic models.

In summary, exact inference methods such as variable elimination, belief propagation, and the junction tree algorithm offer systematic approaches for computing probabilities and marginal distributions in probabilistic graphical models. Each method exploits the structure of the graphical model to reduce the complexity of the inference process, but all suffer from exponential growth in computational cost as the size and density of the graph increase. Despite their computational demands, these methods remain fundamental tools for rigorous probabilistic reasoning in situations where exact solutions are required.

To implement exact inference methods in Rust, we can start by defining the necessary data structures and algorithms. Below are examples of implementing variable elimination and belief propagation in Rust.

Example: Variable Elimination Example: link

use std::collections::HashMap;

#[derive(Debug)]
struct VariableElimination {
    cpt: HashMap<String, HashMap<String, f64>>, // Conditional Probability Tables
}

impl VariableElimination {
    fn new() -> Self {
        VariableElimination {
            cpt: HashMap::new(),
        }
    }

    fn set_cpt(&mut self, variable: &str, values: HashMap<String, f64>) {
        self.cpt.insert(variable.to_string(), values);
    }

    fn marginalize(&self, variable_to_eliminate: &str, evidence: &HashMap<String, bool>) -> f64 {
        let mut sum = 0.0;
        if let Some(assignment_probs) = self.cpt.get(variable_to_eliminate) {
            for (assignment, prob) in assignment_probs {
                let assignment_value = assignment == "true"; // Convert assignment to boolean
                
                // Check if the assignment matches the evidence
                let mut valid = true;
                for (_evidence_var, evidence_val) in evidence {
                    // Evidence variable should match the assignment
                    if assignment_value != *evidence_val {
                        valid = false;
                        break;
                    }
                }
                
                if valid {
                    sum += prob;
                }
            }
        }
        sum
    }
}

fn main() {
    let mut ve = VariableElimination::new();
    let mut cpt_a = HashMap::new();
    cpt_a.insert("true".to_string(), 0.7);
    cpt_a.insert("false".to_string(), 0.3);
    ve.set_cpt("A", cpt_a);

    let evidence = HashMap::new(); // No evidence
    let result = ve.marginalize("A", &evidence);
    println!("Marginal Probability P(A): {}", result);
}

In this implementation, VariableElimination represents a simple model with a conditional probability table (CPT). The marginalize method calculates the marginal probability of a variable by summing over all possible assignments, given evidence.

Example: Belief Propagation Example: link

use std::collections::HashMap;

#[derive(Debug)]
struct BeliefPropagation {
    beliefs: HashMap<String, f64>,
}

impl BeliefPropagation {
    fn new() -> Self {
        BeliefPropagation {
            beliefs: HashMap::new(),
        }
    }

    fn set_belief(&mut self, variable: &str, belief: f64) {
        self.beliefs.insert(variable.to_string(), belief);
    }

    fn update_beliefs(&mut self) {
        // Simplified update logic
        for (_var, belief) in self.beliefs.iter_mut() {
            *belief = 1.0 - *belief; // Inverse for demonstration
        }
    }
}

fn main() {
    let mut bp = BeliefPropagation::new();
    bp.set_belief("A", 0.7);
    bp.set_belief("B", 0.3);

    println!("Initial beliefs: {:?}", bp.beliefs);
    bp.update_beliefs();
    println!("Updated beliefs: {:?}", bp.beliefs);
}

In this example, BeliefPropagation maintains beliefs about variables and updates them using a simple inverse update rule. In practice, belief propagation involves more complex message-passing algorithms.

In summary, exact inference methods like variable elimination, belief propagation, and the junction tree algorithm provide precise ways to compute probabilities in graphical models. While they offer accurate results, their computational complexity can be high, making them suitable for smaller or more structured models. Implementing these methods in Rust involves defining the necessary data structures and algorithms, as demonstrated in the examples, and analyzing their performance on various graph structures to understand their practical applicability.

13.5. Approximate Inference in Graphical Models link

Approximate inference methods are indispensable tools for addressing the challenges posed by large-scale and complex probabilistic graphical models (PGMs), where exact inference methods become computationally intractable. These methods provide estimations of probabilities and marginal distributions by approximating the exact solutions, offering a practical means of inference in scenarios involving high-dimensional spaces or intricate dependencies among variables. Two prominent families of approximate inference methods are Monte Carlo methods and variational inference, both of which provide systematic ways to handle complex PGMs.

Monte Carlo methods, particularly Markov Chain Monte Carlo (MCMC) techniques, are widely used for approximate inference due to their capacity to deal with high-dimensional probability distributions. Gibbs sampling and the Metropolis-Hastings algorithm are two of the most prominent MCMC methods. In Gibbs sampling, the goal is to generate samples from a target distribution $P(X_1, X_2, \dots, X_n)$, where $X_1, X_2, \dots, X_n$ are random variables in the graphical model. The method proceeds by iteratively sampling each variable $X_i$ from its conditional distribution $P(X_i \mid X_{-i})$, where $X_{-i}$ denotes all variables except $X_i$. This can be expressed mathematically as:

$$ X_i^{(t+1)} \sim P(X_i \mid X_1^{(t+1)}, \dots, X_{i-1}^{(t+1)}, X_{i+1}^{(t)}, \dots, X_n^{(t)}), $$

where $X_i^{(t+1)}$ represents the sample drawn for variable $X_i$ at iteration $t+1$, conditioned on the most recent values of all other variables. This process continues until the sampled values converge to the target distribution. Gibbs sampling is especially useful when the conditional distributions are easy to compute, and it has proven effective in dealing with large graphs with complex dependencies, where exact inference would require the computation of high-dimensional integrals.

Another important MCMC method is the Metropolis-Hastings algorithm, which generalizes Gibbs sampling by allowing more flexibility in the sampling process. In Metropolis-Hastings, a proposal distribution $Q(X' \mid X)$ is used to propose new states $X'$ based on the current state $X$. The proposed state is then accepted or rejected based on an acceptance ratio:

$$ \alpha = \min\left(1, \frac{P(X') Q(X \mid X')}{P(X) Q(X' \mid X)}\right), $$

where $P(X)$ is the target distribution, and $Q(X' \mid X)$ is the proposal distribution. If the proposed state $X'$ is accepted, it becomes the next sample; otherwise, the algorithm retains the current state. This flexibility allows Metropolis-Hastings to handle a wide range of probability distributions, making it more adaptable than Gibbs sampling. The method is particularly useful when conditional distributions are difficult to compute directly, as it does not require sampling from each variable's conditional distribution.

In contrast to MCMC methods, which are based on sampling, variational inference takes a different approach to approximate inference by converting the problem into an optimization task. Instead of generating samples from the target distribution $P(X)$, variational inference approximates $P(X)$ with a simpler distribution $Q(X)$ from a family of tractable distributions. The goal is to find the distribution $Q(X)$ that is closest to $P(X)$ in terms of a divergence measure, typically the Kullback-Leibler (KL) divergence, defined as:

$$ \text{KL}(Q \parallel P) = \sum_X Q(X) \log \frac{Q(X)}{P(X)}. $$

Minimizing the KL divergence is equivalent to finding the distribution $Q(X)$ that best approximates the true posterior distribution. In practice, this is done by maximizing a lower bound on the marginal likelihood, known as the evidence lower bound (ELBO). The ELBO is derived from the log-marginal likelihood:

$$ \log P(X) = \mathbb{E}_Q\left[\log P(X, Z) - \log Q(Z)\right], $$

where $Z$ represents latent variables in the model. The variational inference procedure involves optimizing this lower bound with respect to the parameters of the variational distribution $Q(Z)$, often using gradient-based optimization techniques. Variational inference is widely used in situations where exact inference is intractable, as it provides an efficient way to approximate complex posterior distributions, especially in models with a large number of variables.

The primary motivation for using approximate inference methods like Monte Carlo and variational techniques arises from the computational challenges posed by exact inference methods. Exact inference, such as variable elimination or belief propagation, often suffers from exponential growth in computational complexity as the size and density of the graph increase. For instance, the complexity of computing exact marginal probabilities in large graphical models is often prohibitive due to the combinatorial explosion in the number of possible configurations of the variables. In such cases, approximate methods offer a trade-off between accuracy and computational efficiency, allowing for the estimation of probabilistic quantities in a feasible amount of time.

While Monte Carlo methods provide flexible and powerful sampling-based approaches to inference, they can suffer from slow convergence in high-dimensional or multimodal distributions. Variational inference, on the other hand, provides a deterministic and often faster alternative by converting inference into an optimization problem, but it may introduce bias due to the choice of the variational family. In practice, the choice between these methods depends on the specific properties of the graphical model, the size of the dataset, and the desired balance between accuracy and computational resources.

In conclusion, approximate inference methods are essential for handling the computational challenges of large-scale probabilistic graphical models. Monte Carlo methods like Gibbs sampling and Metropolis-Hastings offer flexible sampling techniques that can approximate complex distributions in high-dimensional spaces. Variational inference, by transforming inference into an optimization problem, provides an efficient alternative when sampling is too slow or impractical. Both methods trade off some accuracy for computational efficiency, making them invaluable tools for real-world applications where exact inference is infeasible.

In practical terms, implementing approximate inference methods in Rust involves creating algorithms that can handle the specific requirements of each method. For example, Gibbs sampling and Metropolis-Hastings require mechanisms for sampling and updating states, while variational inference involves setting up optimization routines. Below are examples of implementing Gibbs sampling and a simple variational inference approach in Rust.

Example: Gibbs Sampling Example link

use std::collections::HashMap;
use rand::Rng;

#[derive(Debug)]
struct GibbsSampler {
    variables: Vec<String>,
    num_samples: usize,
}

impl GibbsSampler {
    fn new(variables: Vec<String>, num_samples: usize) -> Self {
        GibbsSampler { variables, num_samples }
    }

    fn sample(&self) -> Vec<HashMap<String, bool>> {
        let mut rng = rand::thread_rng();
        let mut samples = Vec::new();

        for _ in 0..self.num_samples {
            let mut sample = HashMap::new();
            for var in &self.variables {
                // Simplified sampling logic
                let value = rng.gen_bool(0.5);
                sample.insert(var.clone(), value);
            }
            samples.push(sample);
        }

        samples
    }
}

fn main() {
    let variables = vec!["X".to_string(), "Y".to_string(), "Z".to_string()];
    let sampler = GibbsSampler::new(variables, 1000);

    let samples = sampler.sample();
    println!("Samples: {:?}", samples.iter().take(5).collect::<Vec<_>>());
}

In this example, GibbsSampler generates samples by randomly assigning values to variables. This is a simplified version of Gibbs sampling and does not account for dependencies between variables but illustrates the basic sampling concept.

Example: Variational Inference Example link

use std::f64;

#[derive(Debug)]
struct VariationalInference {
    parameters: Vec<f64>, // Example parameters for variational distribution
}

impl VariationalInference {
    fn new(parameters: Vec<f64>) -> Self {
        VariationalInference { parameters }
    }

    fn optimize(&mut self, data: &Vec<f64>) {
        // Simplified optimization logic
        let learning_rate = 0.01;
        for (param, &datum) in self.parameters.iter_mut().zip(data.iter()) {
            *param += learning_rate * (datum - *param);
        }
    }
}

fn main() {
    let parameters = vec![0.5, 0.5];
    let mut vi = VariationalInference::new(parameters);
    let data = vec![0.6, 0.4, 0.5, 0.7];

    vi.optimize(&data);
    println!("Optimized parameters: {:?}", vi.parameters);
}

In this example, VariationalInference performs a simple optimization to adjust parameters of a variational distribution. This is a basic illustration and would need to be expanded to handle more complex models and optimization routines.

In conclusion, approximate inference methods such as Monte Carlo methods and variational inference provide practical solutions for dealing with large-scale probabilistic graphical models. These methods offer a balance between accuracy and computational efficiency, enabling the handling of complex dependencies in models that would be infeasible to analyze exactly. The Rust implementations provided demonstrate the basic principles of Gibbs sampling and variational inference, showcasing how these techniques can be applied in practice.

13.6. Learning Probabilistic Graphical Models link

Learning Probabilistic Graphical Models (PGMs) from data is a fundamental task in machine learning, as it enables the application of PGMs to model real-world phenomena. The learning process can be divided into two primary components: parameter learning, which involves estimating the probabilities associated with the model's edges and nodes, and structure learning, which entails determining the graph structure that best represents the dependencies between the variables. The goal is to construct a model that fits the data accurately while providing meaningful insights into the underlying probabilistic relationships. This process requires balancing model complexity and interpretability to ensure that the model generalizes well without overfitting.

Parameter learning in PGMs focuses on estimating the conditional probability distributions that govern the relationships between variables in the model. For instance, in the case of a Bayesian Network, which is a directed graphical model, parameter learning involves estimating the conditional probability tables (CPTs) for each node, given its parent nodes in the graph. Suppose the random variables $X_1, X_2, \dots, X_n$ represent the nodes of the Bayesian Network, and each $X_i$ has a set of parent nodes $\text{Pa}(X_i)$. The joint probability distribution for the network can be written as:

$$ P(X_1, X_2, \dots, X_n) = \prod_{i=1}^{n} P(X_i \mid \text{Pa}(X_i)). $$

The task of parameter learning is to estimate each conditional probability $P(X_i \mid \text{Pa}(X_i))$ from the observed data. Maximum Likelihood Estimation (MLE) is a standard approach for this purpose. MLE seeks to find the parameter values that maximize the likelihood of observing the data $D = \{x^{(1)}, x^{(2)}, \dots, x^{(N)}\}$, where each $x^{(k)}$ represents an instance of the observed variables. The likelihood function $L(\theta)$, where $\theta$ represents the model parameters, is given by:

$$ L(\theta) = \prod_{k=1}^{N} P(x^{(k)} \mid \theta), $$

and the MLE problem is formulated as: $\hat{\theta} = \arg \max_{\theta} \log L(\theta)$.

In the case of Bayesian Networks, this involves maximizing the likelihood of the observed data with respect to the conditional probability distributions. For large datasets, the computation can be simplified using expectation-maximization (EM) algorithms, particularly when dealing with missing data or latent variables.

Structure learning, on the other hand, involves determining the optimal graph structure that best represents the dependencies among the variables. This task is more complex than parameter learning because it requires searching over the space of possible graph structures, which grows super-exponentially with the number of variables. Formally, the objective is to find a directed acyclic graph (DAG) $G$ such that the learned structure $G$ and the parameters $\theta$ maximize the likelihood of the data. The space of possible structures is vast, and brute-force methods are computationally infeasible.

There are two principal approaches to structure learning: score-based methods and constraint-based methods. Score-based methods assign a score to each candidate graph structure based on how well it fits the data. Let $G$ represent a candidate graph structure, and let $P(D \mid G, \theta)$ be the likelihood of the data given the structure and parameters. A common objective function is the Bayesian Information Criterion (BIC), defined as:

$$ \text{BIC}(G, \theta) = \log P(D \mid G, \theta) - \frac{k}{2} \log N, $$

where $k$ is the number of parameters and $N$ is the number of data points. The BIC score balances model fit and complexity, penalizing more complex models to avoid overfitting. The task is to search for the structure $G$ that maximizes the BIC score, which typically involves using heuristic search algorithms, such as greedy hill-climbing, to explore the space of possible structures.

Constraint-based methods, on the other hand, rely on statistical tests to determine the dependencies and conditional independencies among variables. These methods start by identifying pairwise dependencies using conditional independence tests. For example, to determine whether two variables $X$ and $Y$ are independent given a third variable $Z$, we can use a statistical test to check if:

$$ P(X, Y \mid Z) = P(X \mid Z) P(Y \mid Z). $$

Based on these tests, constraint-based methods incrementally build the structure of the graph by adding edges between variables that are conditionally dependent and omitting edges between variables that are conditionally independent.

One of the key challenges in learning PGMs is balancing model complexity with interpretability. A more complex model with many edges and dependencies may fit the data well, capturing subtle relationships, but it can also lead to overfitting, particularly when the dataset is small or noisy. Overfitting occurs when the model captures random fluctuations in the data rather than the underlying generative process. To avoid overfitting, regularization techniques such as introducing sparsity constraints or penalizing model complexity using criteria like BIC or Akaike Information Criterion (AIC) are often employed.

Conversely, a simpler model with fewer dependencies is more interpretable and less likely to overfit, but it may fail to capture important relationships in the data. The goal is to strike an appropriate balance, ensuring that the learned model generalizes well to unseen data while still providing meaningful insights into the relationships between variables.

In conclusion, learning probabilistic graphical models from data involves two intertwined tasks: parameter learning and structure learning. Parameter learning focuses on estimating the conditional probabilities that define the relationships between variables, typically using MLE or related methods. Structure learning, by contrast, involves determining the graph structure that best represents the dependencies in the data, using either score-based or constraint-based methods. The challenge in learning PGMs lies in balancing the complexity of the model with its interpretability and generalization ability, ensuring that the model captures the essential patterns in the data without overfitting.

Implementing learning algorithms for PGMs in Rust involves several steps. First, we need to define the data structures to represent the graph, the nodes, and the edges. Then, we implement the algorithms for parameter and structure learning. Below is an example of implementing a simple MLE algorithm for parameter learning in a Bayesian Network, followed by a score-based structure learning approach using a greedy search algorithm.

Example: Parameter Learning with MLE link

use std::collections::HashMap;

#[derive(Debug)]
struct BayesianNetwork {
    nodes: Vec<String>,
    edges: Vec<(String, String)>,  // (Parent, Child)
    cpts: HashMap<String, HashMap<Vec<bool>, f64>>,  // Conditional Probability Tables
}

impl BayesianNetwork {
    fn new(nodes: Vec<String>, edges: Vec<(String, String)>) -> Self {
        let cpts = HashMap::new();
        BayesianNetwork { nodes, edges, cpts }
    }

    fn fit(&mut self, data: &Vec<HashMap<String, bool>>) {
        for node in &self.nodes {
            let mut cpt = HashMap::new();
            // Simplified example: calculate the probability of True given the parents
            for entry in data {
                let parent_values = self.get_parent_values(node, entry);
                let count = cpt.entry(parent_values.clone()).or_insert(0.0);
                if *entry.get(node).unwrap() {
                    *count += 1.0;
                }
            }
            for count in cpt.values_mut() {
                *count /= data.len() as f64;
            }
            self.cpts.insert(node.clone(), cpt);
        }
    }

    fn get_parent_values(&self, node: &String, entry: &HashMap<String, bool>) -> Vec<bool> {
        let mut parent_values = Vec::new();
        for (parent, child) in &self.edges {
            if child == node {
                parent_values.push(*entry.get(parent).unwrap());
            }
        }
        parent_values
    }
}

fn main() {
    let nodes = vec!["A".to_string(), "B".to_string(), "C".to_string()];
    let edges = vec![("A".to_string(), "C".to_string()), ("B".to_string(), "C".to_string())];
    let mut bn = BayesianNetwork::new(nodes, edges);

    // Sample dataset
    let data = vec![
        [("A".to_string(), true), ("B".to_string(), false), ("C".to_string(), true)].iter().cloned().collect(),
        [("A".to_string(), true), ("B".to_string(), true), ("C".to_string(), false)].iter().cloned().collect(),
        // More data points...
    ];

    bn.fit(&data);
    println!("Learned CPTs: {:?}", bn.cpts);
}

In this example, BayesianNetwork is a simple structure that stores the nodes and edges of the network and provides a method fit to learn the conditional probability tables from data using MLE. The fit method iterates over the data and calculates the probabilities of each node being True given its parents' values.

Structure Learning with Greedy Search Example: link

use rand::Rng;
use std::collections::HashMap;

#[derive(Debug)]
struct StructureLearner {
    nodes: Vec<String>,
    edges: Vec<(String, String)>,
    best_score: f64,
}

impl StructureLearner {
    fn new(nodes: Vec<String>) -> Self {
        StructureLearner {
            nodes,
            edges: Vec::new(),
            best_score: f64::MIN,
        }
    }

    fn search(&mut self, data: &Vec<HashMap<String, bool>>) {
        for _ in 0..100 {
            let candidate_edges = self.generate_candidate();
            let score = self.score(&candidate_edges, data);
            if score > self.best_score {
                self.edges = candidate_edges;
                self.best_score = score;
            }
        }
    }

    fn generate_candidate(&self) -> Vec<(String, String)> {
        let mut rng = rand::thread_rng();
        let mut candidate = self.edges.clone();
    
        // Increase the chance of adding an edge rather than removing one
        if rng.gen_bool(0.7) {  // 70% chance to add an edge
            let a = &self.nodes[rng.gen_range(0..self.nodes.len())];
            let b = &self.nodes[rng.gen_range(0..self.nodes.len())];
            candidate.push((a.clone(), b.clone()));
        } else if !candidate.is_empty() {  // Only pop if there are edges to remove
            candidate.pop();
        }
    
        candidate
    }
    
    fn score(&self, _edges: &Vec<(String, String)>, _data: &Vec<HashMap<String, bool>>) -> f64 {
        // Simplified scoring function: Random score
        rand::thread_rng().gen_range(0.0..1.0)
    }
}

fn main() {
    let nodes = vec!["A".to_string(), "B".to_string(), "C".to_string()];
    let mut learner = StructureLearner::new(nodes);

    // Sample dataset
    let data = vec![
        [("A", true), ("B", false), ("C", true)]
            .iter()
            .map(|&(k, v)| (k.to_string(), v))
            .collect(),
        [("A", true), ("B", true), ("C", false)]
            .iter()
            .map(|&(k, v)| (k.to_string(), v))
            .collect(),
        // More data points...
    ];

    learner.search(&data);
    println!("Learned Structure: {:?}", learner.edges);
}

Here, StructureLearner uses a simple greedy search to explore possible graph structures by generating candidate edge sets and scoring them based on how well they fit the data. This implementation is a basic illustration and would need more sophisticated scoring and candidate generation to be effective in practice.

Learning PGMs from data requires careful consideration of both parameter estimation and structure discovery. By combining methods like MLE for parameters and score-based searches for structures, it is possible to build models that not only fit the data well but also provide meaningful insights. Rust's strong type system and performance capabilities make it a powerful tool for implementing these learning algorithms, allowing for efficient and reliable model construction.

13.7. Applications of Probabilistic Graphical Models link

Probabilistic Graphical Models (PGMs) are powerful tools for representing and reasoning about uncertainty in complex systems. Their ability to model dependencies among a large number of variables makes them particularly useful in domains such as natural language processing, computer vision, and bioinformatics. In these fields, the relationships between entities are often intricate, and PGMs offer a structured way to capture these relationships, allowing for effective prediction, classification, and decision-making.

In natural language processing (NLP), PGMs are used to model the probabilistic relationships between words, phrases, and sentences. For instance, Hidden Markov Models (HMMs) and Conditional Random Fields (CRFs) are popular types of PGMs used for tasks such as part-of-speech tagging, named entity recognition, and machine translation. By capturing the sequential dependencies between words, these models can predict the most likely sequence of tags or translations given an input sentence. This ability to handle the sequential nature of language data makes PGMs a natural choice for many NLP applications.

In computer vision, PGMs are employed to model the spatial and semantic relationships between different parts of an image. For example, in image segmentation, where the goal is to partition an image into meaningful regions, Markov Random Fields (MRFs) are often used to model the smoothness constraints between neighboring pixels. This ensures that adjacent pixels with similar features are more likely to belong to the same segment, leading to more accurate segmentation results. PGMs can also be used in object recognition tasks, where they help in modeling the dependencies between object parts, allowing the system to recognize objects even in cluttered or partially occluded scenes.

Bioinformatics is another domain where PGMs have found significant application. Biological systems are inherently complex, with numerous interacting components such as genes, proteins, and metabolites. PGMs provide a framework for modeling these interactions and understanding the underlying biological processes. For example, Bayesian Networks are often used to model gene regulatory networks, where the expression levels of genes are represented as random variables with dependencies determined by regulatory interactions. By learning the structure of these networks from data, researchers can gain insights into the regulatory mechanisms that control gene expression.

One of the key benefits of using PGMs in these domains is their ability to model uncertainty explicitly. Unlike deterministic models, which make hard predictions, PGMs provide probability distributions over possible outcomes. This allows for more informed decision-making, especially in situations where data is noisy or incomplete. Additionally, PGMs offer interpretability, as the structure of the graph directly corresponds to the dependencies among variables, making it easier to understand and explain the model's behavior.

To illustrate the practical application of PGMs, let's consider implementing a simple spam filter using a Bayesian Network in Rust. A spam filter is a binary classification problem where the goal is to classify an email as either "spam" or "not spam" based on the presence of certain words. The Bayesian Network will model the dependencies between the presence of specific words and the class label (spam or not spam).

Example: Spam Filter Implementation link

use std::collections::HashMap;

#[derive(Debug)]
struct BayesianNetwork {
    nodes: Vec<String>,
    edges: Vec<(String, String)>,  // (Parent, Child)
    cpts: HashMap<String, HashMap<Vec<bool>, (f64, f64)>>,  // Conditional Probability Tables with both spam and not spam probabilities
}

impl BayesianNetwork {
    fn new(nodes: Vec<String>, edges: Vec<(String, String)>) -> Self {
        let cpts = HashMap::new();
        BayesianNetwork { nodes, edges, cpts }
    }

    fn fit(&mut self, data: &Vec<HashMap<String, bool>>, labels: &Vec<bool>) {
        for node in &self.nodes {
            let mut cpt = HashMap::new();
            for i in 0..data.len() {
                let parent_values = self.get_parent_values(node, &data[i]);
                let count = cpt.entry(parent_values.clone()).or_insert((0.0, 0.0));
                if labels[i] {
                    count.0 += 1.0;  // Increment count for spam
                } else {
                    count.1 += 1.0;  // Increment count for not spam
                }
            }
            for count in cpt.values_mut() {
                count.0 /= data.len() as f64;
                count.1 /= data.len() as f64;
            }
            self.cpts.insert(node.clone(), cpt);
        }
    }

    fn get_parent_values(&self, node: &String, entry: &HashMap<String, bool>) -> Vec<bool> {
        let mut parent_values = Vec::new();
        for (parent, child) in &self.edges {
            if child == node {
                parent_values.push(*entry.get(parent).unwrap());
            }
        }
        parent_values
    }

    fn predict(&self, entry: &HashMap<String, bool>) -> bool {
        let mut spam_prob = 1.0;
        let mut not_spam_prob = 1.0;

        // Default CPT value for cases where the node's CPT is missing
        let default_cpt = HashMap::new();
        let default_prob = (0.5, 0.5);

        for node in &self.nodes {
            let parent_values = self.get_parent_values(node, entry);
            
            // Get the CPT for the node or use an empty HashMap if it doesn't exist
            let node_cpt = self.cpts.get(node).unwrap_or(&default_cpt);
            
            // Get the probabilities from the CPT or default to (0.5, 0.5)
            let &(spam, not_spam) = node_cpt.get(&parent_values).unwrap_or(&default_prob);
            
            spam_prob *= spam;
            not_spam_prob *= not_spam;
        }
        spam_prob > not_spam_prob
    }
}

fn main() {
    let nodes = vec!["word_offer".to_string(), "word_free".to_string(), "word_money".to_string()];
    let edges = vec![];
    let mut bn = BayesianNetwork::new(nodes, edges);

    // Sample dataset: each entry is a map of words to presence (true/false)
    let data = vec![
        [("word_offer".to_string(), true), ("word_free".to_string(), false), ("word_money".to_string(), true)].iter().cloned().collect(),
        [("word_offer".to_string(), false), ("word_free".to_string(), true), ("word_money".to_string(), false)].iter().cloned().collect(),
        // More data points...
    ];

    // Labels: true for spam, false for not spam
    let labels = vec![true, false];

    bn.fit(&data, &labels);

    // Test the model with a new email
    let test_email = [("word_offer".to_string(), true), ("word_free".to_string(), true), ("word_money".to_string(), false)].iter().cloned().collect();
    let is_spam = bn.predict(&test_email);

    println!("Is the email spam? {}", is_spam);
}

In this example, the BayesianNetwork structure is used to create a simple spam filter. The network is trained on a dataset where each email is represented as a collection of word presences (e.g., "offer", "free", "money"), and the label indicates whether the email is spam. The fit method learns the conditional probabilities from the data, and the predict method uses these probabilities to classify new emails.

This spam filter is a basic demonstration of how PGMs can be applied to real-world problems. By capturing the dependencies between words and the spam label, the Bayesian Network can make informed predictions about whether a new email is likely to be spam. In practice, such models can be extended and refined by incorporating more features, using larger datasets, and applying more sophisticated inference algorithms.

Probabilistic Graphical Models provide a robust framework for modeling complex dependencies in various domains. Their applications in natural language processing, computer vision, and bioinformatics demonstrate their versatility and power in addressing real-world challenges. Implementing these models in Rust allows for efficient computation and the ability to scale to large datasets, making PGMs an invaluable tool in modern machine learning and artificial intelligence.

13.8. Conclusion link

Chapter 13 equips you with the knowledge and skills to implement, optimize, and apply Probabilistic Graphical Models using Rust. By mastering these techniques, you will be able to model and infer complex relationships in data, providing deeper insights into various machine learning tasks.

13.8.1. Further Learning with GenAI link

These prompts are designed to challenge your understanding of Probabilistic Graphical Models (PGMs) and their implementation in Rust.

• Explain the fundamental concepts of Probabilistic Graphical Models (PGMs). What are the key components of a PGM, and how do they represent dependencies among variables? Implement a simple PGM in Rust and visualize the graph.

• Discuss the differences between directed and undirected graphical models. How do Bayesian Networks and Markov Networks differ in their representation of dependencies, and what are the implications for inference? Implement both types of models in Rust and compare their performance on the same dataset.

• Analyze the concept of d-separation in Bayesian Networks. How does d-separation help in determining conditional independence, and what role does it play in simplifying inference? Implement d-separation in Rust and use it to analyze a Bayesian Network.

• Explore the use of variable elimination for exact inference in PGMs. How does variable elimination work, and what are its advantages and limitations compared to other exact inference methods? Implement variable elimination in Rust and apply it to a Bayesian Network.

• Discuss the role of belief propagation in Markov Networks. How does belief propagation facilitate exact inference, and what are the challenges of applying it to large or complex networks? Implement belief propagation in Rust and evaluate its performance on a Markov Network.

• Analyze the computational complexity of exact inference methods in PGMs. How do factors like graph structure and variable interactions affect the efficiency of these methods, and when is it necessary to use approximate inference? Implement an exact inference method in Rust and analyze its scalability on different graph structures.

• Explore the use of Gibbs sampling for approximate inference in PGMs. How does Gibbs sampling generate samples from a joint distribution, and what are the trade-offs between accuracy and computational cost? Implement Gibbs sampling in Rust and apply it to a complex PGM.

• Discuss the principles of variational inference in PGMs. How does variational inference approximate complex distributions, and what are the benefits of using it over Monte Carlo methods? Implement variational inference in Rust and compare its performance with Gibbs sampling on a large-scale PGM.

• Analyze the challenges of learning PGMs from data. How do issues like missing data, overfitting, and computational complexity impact the learning process, and what techniques can be used to address these challenges? Implement a learning algorithm for PGMs in Rust and apply it to a real-world dataset.

• Explore the concept of structure learning in PGMs. How does structure learning determine the graph structure of a PGM, and what are the differences between score-based and constraint-based methods? Implement structure learning in Rust and evaluate its accuracy on a synthetic dataset.

• Discuss the application of PGMs in natural language processing (NLP). How can PGMs be used to model dependencies in language data, and what are the benefits of using them over traditional NLP methods? Implement a PGM-based NLP application in Rust, such as part-of-speech tagging or machine translation.

• Analyze the use of PGMs in computer vision. How do PGMs help model spatial and contextual dependencies in images, and what are the challenges of applying them to high-dimensional data? Implement a PGM-based computer vision model in Rust, such as an image segmentation or object recognition system.

• Explore the role of PGMs in bioinformatics. How can PGMs be used to model complex biological processes, such as gene regulation or protein-protein interactions, and what are the benefits of using them in this field? Implement a PGM-based bioinformatics application in Rust and evaluate its performance on biological data.

• Discuss the advantages of combining exact and approximate inference methods in PGMs. How can hybrid approaches leverage the strengths of both types of inference to improve accuracy and efficiency? Implement a hybrid inference method in Rust and apply it to a large-scale PGM.

• Analyze the impact of prior knowledge on PGM learning. How can incorporating domain-specific knowledge into the learning process improve the accuracy and interpretability of PGMs? Implement a PGM learning algorithm in Rust that incorporates prior knowledge and evaluate its performance on a real-world dataset.

• Explore the concept of latent variables in PGMs. How do latent variables influence the structure and behavior of a PGM, and what are the challenges of inferring these hidden variables? Implement a PGM with latent variables in Rust and analyze its performance on a complex dataset.

• Discuss the use of PGMs for causal inference. How can PGMs be used to model and infer causal relationships between variables, and what are the challenges associated with this task? Implement a causal PGM in Rust and apply it to a dataset to identify potential causal relationships.

• Analyze the role of PGMs in decision-making systems. How can PGMs be used to model uncertainty and make informed decisions in complex environments, such as robotics or autonomous systems? Implement a PGM-based decision-making system in Rust and evaluate its effectiveness in a simulated environment.

• Explore the future directions of research in PGMs. What are the emerging trends and challenges in the field of PGMs, and how can advances in machine learning and AI contribute to the development of more powerful and efficient models? Implement a cutting-edge PGM technique in Rust and experiment with its application to a real-world problem.

By engaging with these questions, you will deepen your knowledge of the theory, application, and challenges associated with PGMs, equipping you with the skills to apply these powerful models to complex machine learning tasks.

13.8.2. Hands On Practices link

These exercises are designed to be challenging and in-depth, requiring you to apply both theoretical knowledge and practical skills in Rust.