15.1. Introduction to Kernel Methods link

Kernel methods are a fundamental class of techniques in machine learning that allow algorithms to operate effectively in high-dimensional feature spaces without explicitly transforming the data into those spaces. The core mathematical innovation underlying kernel methods is the kernel trick, a technique that allows the computation of inner products in an implicitly transformed high-dimensional space without directly computing the coordinates of the transformed data points. This capability is particularly advantageous because, in many cases, explicitly mapping data into high-dimensional spaces would be computationally prohibitive due to the exponential increase in the number of features. However, by leveraging the kernel trick, machine learning algorithms can still exploit the benefits of operating in these spaces without incurring the associated computational costs.

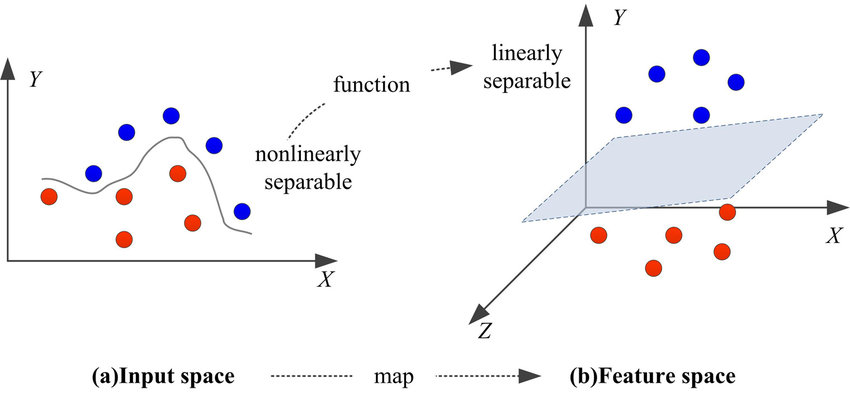
Figure 1: Kernel trick in Machine learning.

The kernel trick works by replacing the standard inner product of two data points in the original feature space $x$ and $x'$ with a kernel function $k(x, x')$, which computes the inner product in a higher-dimensional space:

$$ k(x, x') = \langle \phi(x), \phi(x') \rangle, $$

where $\phi(x)$ is a feature mapping that transforms the input data $x$ into a high-dimensional space. Importantly, the kernel function allows us to compute this inner product without ever explicitly computing $\phi(x)$, as long as we know $k(x, x')$. This avoids the computational complexity of dealing with high-dimensional vectors directly, while still allowing the learning algorithm to operate in a richer feature space. The kernel trick is a general technique and can be applied to a wide range of machine learning algorithms, including Support Vector Machines (SVM), principal component analysis (PCA), and others.

Kernel methods are especially important in classification and regression tasks because they provide a way to extend linear models to handle non-linear relationships in the data. In many cases, linear models assume that the data can be separated or modeled by a hyperplane in the original feature space. For example, in binary classification using SVM, the goal is to find a hyperplane that separates the two classes. This is feasible when the data is linearly separable, but many real-world datasets exhibit non-linear relationships that cannot be captured by a simple hyperplane. Kernel methods resolve this issue by implicitly transforming the data into a higher-dimensional space where linear separation may become possible. The decision boundary in the original space, which may be non-linear, corresponds to a linear decision boundary in the higher-dimensional space.

To understand this formally, consider a binary classification problem where the goal is to find a hyperplane that separates two classes. In the context of an SVM, the hyperplane is represented as:

$$ w^T x + b = 0, $$

where $w$ is the weight vector and $b$ is the bias. The decision function for a new data point $x$ is given by:

$$ f(x) = \text{sign}(w^T x + b). $$

In a non-linear problem, the data points may not be separable by a hyperplane in the original feature space. However, by applying a non-linear transformation $\phi(x)$, we map the data into a higher-dimensional space where a linear hyperplane can be used:

$$ w^T \phi(x) + b = 0. $$

The kernel trick allows us to compute the dot product $\langle \phi(x), \phi(x') \rangle$ using a kernel function $k(x, x')$, thus enabling the SVM to find a non-linear decision boundary in the original space. The corresponding decision function becomes:

$$ f(x) = \text{sign}\left( \sum_{i=1}^{N} \alpha_i y_i k(x_i, x) + b \right), $$

where $\alpha_i$ are the Lagrange multipliers from the dual formulation of the SVM optimization problem, and $y_i$ are the class labels. The kernel function $k(x, x')$ defines the nature of the decision boundary, and the choice of kernel can significantly affect the model's performance.

The power of kernel methods lies in their ability to transform linear algorithms into non-linear ones without requiring explicit transformations of the data. By applying the kernel trick, we can handle complex relationships between features in high-dimensional spaces efficiently. Moreover, kernel methods provide a flexible framework that allows practitioners to choose different kernel functions depending on the problem at hand. This adaptability makes kernel methods indispensable in fields such as computer vision, bioinformatics, and natural language processing, where non-linear patterns frequently arise.

In conclusion, kernel methods provide a robust and flexible framework for tackling non-linear problems in machine learning. The kernel trick enables algorithms to operate in high-dimensional spaces without explicitly computing the feature transformations, allowing for efficient learning in complex environments. By selecting appropriate kernel functions, machine learning algorithms such as Support Vector Machines can model non-linear relationships in data, offering significant improvements over traditional linear approaches. This capability is especially crucial in real-world applications where data exhibits complex patterns that cannot be captured by linear models.

To illustrate kernel methods in practice, we can implement a simple kernelized linear regression model in Rust. This implementation will utilize the RBF kernel, which is often used due to its locality properties and ability to handle non-linear relationships effectively. We will also apply this model to a dataset to observe the effects of using different kernels.

First, let’s implement the kernel function in Rust. The RBF kernel is defined as follows:

fn rbf_kernel(x1: &[f64], x2: &[f64], gamma: f64) -> f64 {
    let squared_diff: f64 = x1.iter().zip(x2.iter())
        .map(|(a, b)| (a - b).powi(2))
        .sum();
    (-gamma * squared_diff).exp()
}

In this code, the rbf_kernel function computes the RBF kernel between two vectors x1 and x2, with gamma controlling the spread of the kernel. A lower value of gamma results in a smoother decision boundary, while a higher value leads to a more complex decision boundary.

Next, we will implement a simple kernelized linear regression model. For the sake of brevity, we will focus on the essential components of the model.

struct KernelizedLinearRegression {
    alpha: Vec<f64>,
    support_vectors: Vec<Vec<f64>>,
    gamma: f64,
}

impl KernelizedLinearRegression {
    fn new(gamma: f64) -> Self {
        KernelizedLinearRegression {
            alpha: Vec::new(),
            support_vectors: Vec::new(),
            gamma,
        }
    }

    fn fit(&mut self, X: Vec<Vec<f64>>, y: Vec<f64>) {
        // Store support vectors and their corresponding alpha values
        self.support_vectors = X.clone();
        self.alpha = vec![0.0; X.len()]; // Placeholder for dual coefficients
        // Implement fitting logic here (e.g., optimization routine)
    }

    fn predict(&self, x: Vec<f64>) -> f64 {
        self.support_vectors.iter()
            .zip(self.alpha.iter())
            .map(|(sv, &alpha)| alpha * rbf_kernel(sv, &x, self.gamma))
            .sum()
    }
}

In this example, the KernelizedLinearRegression struct contains fields for the dual coefficients (alpha), support vectors, and the hyperparameter gamma. The fit method is where the model would learn from the data, and the predict method uses the kernel function to compute predictions based on the support vectors.

To see the effects of different kernels, one can experiment with various kernel functions and their parameters. For instance, we can implement a polynomial kernel as follows:

fn main() {
    let x1 = vec![1.0, 2.0, 3.0];
    let x2 = vec![4.0, 5.0, 6.0];
    let degree = 2;

    let result = polynomial_kernel(&x1, &x2, degree);
    println!("Polynomial Kernel result: {}", result);
}

fn polynomial_kernel(x1: &[f64], x2: &[f64], degree: i32) -> f64 {
    if x1.len() != x2.len() {
        panic!("Input vectors must have the same length");
    }
    let dot_product: f64 = x1.iter().zip(x2.iter()).map(|(a, b)| a * b).sum();
    (dot_product + 1.0).powi(degree)
}

Choosing the right kernel is critical to achieving optimal performance. The choice depends on the characteristics of the data and the specific problem at hand. By experimenting with different kernels, one can gain insights into how the model behaves and adapts to the underlying data structure.

In conclusion, kernel methods are an essential topic in machine learning, offering a robust framework for handling complex, non-linear relationships through the use of the kernel trick. Their flexibility and adaptability make them a valuable tool for practitioners. By implementing kernel methods in Rust, we can leverage their power while enjoying the performance benefits of a systems programming language. As we continue through this chapter, we will explore more advanced applications and techniques involving kernel methods, solidifying our understanding and proficiency in this vital area of machine learning.

15.2. Kernel Functions link

Kernel methods have become a powerful tool in machine learning due to their ability to transform linear algorithms into more flexible and expressive models capable of handling non-linear data. At the heart of these methods lie kernel functions, which measure the similarity between two data points in an implicit, higher-dimensional feature space. Instead of explicitly transforming the data into this feature space, kernel functions allow algorithms to compute the inner products of the transformed data points efficiently. This characteristic enables machine learning models, such as support vector machines (SVMs), to handle non-linearly separable data without a significant computational burden. In this section, we explore several common kernel functions, their mathematical foundations, and their practical advantages and disadvantages, followed by an implementation in Rust for classification tasks.

The linear kernel is the simplest and most intuitive of the kernel functions, operating in the original feature space by computing the dot product between two vectors. Mathematically, the linear kernel is expressed as:

$$ K(x, y) = x^T y, $$

where $x$ and $y$ are feature vectors. The linear kernel is effective in cases where the data is already linearly separable, making it suitable for tasks where a linear decision boundary suffices. However, the main limitation of the linear kernel is its inability to capture complex relationships between data points, particularly in scenarios where the data exhibits non-linear patterns. In such cases, a linear classifier will likely underperform, as it cannot model the non-linear separability inherent in the data.

To address this limitation, non-linear kernel functions are employed, one of which is the polynomial kernel. The polynomial kernel extends the capabilities of the linear kernel by introducing polynomial terms, allowing the model to capture non-linear relationships between data points. The polynomial kernel is mathematically defined as:

$$ K(x, y) = (x^T y + c)^d, $$

where $c$ is a constant, and $d$ is the degree of the polynomial. The choice of $d$ determines the complexity of the decision boundary: a higher degree ddd results in more complex decision boundaries, while lower values of $d$ produce simpler boundaries. One advantage of the polynomial kernel is its ability to model data with polynomial-like relationships. However, the choice of degree $d$ is critical, as setting $d$ too high can lead to overfitting, where the model becomes overly sensitive to the training data and fails to generalize to new examples. Conversely, a low degree $d$ may underfit the data, resulting in poor predictive performance.

Another widely used kernel function is the Gaussian kernel, also known as the Radial Basis Function (RBF) kernel. The RBF kernel is particularly effective in situations where the data exhibits highly non-linear relationships, as it transforms the input data into an infinite-dimensional space. The Gaussian kernel is defined as:

$$ K(x, y) = \exp\left( -\frac{|x - y|^2}{2 \sigma^2} \right), $$

where $\sigma$ is a parameter that controls the width of the kernel. The RBF kernel has several desirable properties, one of which is its ability to capture complex and subtle patterns in the data, making it highly versatile in various applications. By mapping the data into an infinite-dimensional space, the RBF kernel allows for the possibility of perfect separation between classes in this transformed space. However, the performance of the RBF kernel is sensitive to the choice of $\sigma$. If $\sigma$ is set too large, the decision boundary becomes too smooth, leading to underfitting. On the other hand, if $\sigma$ is too small, the decision boundary becomes overly complex, increasing the risk of overfitting.

The sigmoid kernel, which resembles the activation function used in neural networks, is another kernel function employed in machine learning. It is defined as:

$$ K(x, y) = \tanh(\alpha x^T y + c), $$

where $\alpha$ and $c$ are hyperparameters. The sigmoid kernel can model certain types of relationships, particularly those that are similar to neural network architectures. However, in many practical scenarios, the sigmoid kernel tends to perform poorly compared to other kernels, such as the polynomial or RBF kernels. One of the reasons for this is that the sigmoid kernel is not guaranteed to be a positive semi-definite kernel, which can lead to optimization issues during model training, particularly in support vector machines.

The choice of kernel function plays a crucial role in determining the performance of kernel-based machine learning algorithms. Each kernel brings its own advantages and disadvantages, and the appropriate choice depends on the nature of the data and the specific task at hand. For example, if the data is linearly separable, the linear kernel provides a simple and computationally efficient solution. If the data exhibits polynomial relationships, the polynomial kernel can model the decision boundary effectively. For highly complex and non-linear data, the Gaussian RBF kernel is often the best choice, as it can capture intricate patterns by mapping the data into a high-dimensional space.

In Rust, implementing kernel functions for classification tasks involves designing efficient routines for computing the inner products in the transformed space. For instance, the linear kernel can be implemented using simple vector dot products, while the polynomial kernel requires the additional computation of powers and constant terms. The RBF kernel, being more computationally intensive, involves calculating the squared Euclidean distance between data points and applying the exponential function. Rust’s performance and concurrency features make it well-suited for implementing these kernel functions in large-scale machine learning tasks, allowing for efficient computation even when dealing with high-dimensional data.

In conclusion, kernel methods provide a flexible and powerful framework for handling non-linear relationships in machine learning. By using kernel functions to implicitly transform data into higher-dimensional spaces, algorithms such as SVMs can operate on data that is not linearly separable in its original form. The choice of kernel function is critical and must be made carefully based on the nature of the data and the complexity of the relationships within it. Through the use of appropriate kernel functions, machine learning models can achieve better generalization and performance, particularly in challenging classification tasks where linear models fall short.

To illustrate the practical implementation of these kernel functions in Rust, let us begin by defining each kernel function. We can create a module named kernels in Rust that contains implementations for the linear, polynomial, Gaussian, and sigmoid kernels. The following code outlines how to define these kernel functions in Rust.

mod kernels {
    pub fn linear(x: &[f64], y: &[f64]) -> f64 {
        if x.len() != y.len() {
            panic!("Input vectors must have the same length");
        }
        x.iter().zip(y.iter()).map(|(xi, yi)| xi * yi).sum()
    }

    pub fn polynomial(x: &[f64], y: &[f64], c: f64, d: i32) -> f64 {
        if x.len() != y.len() {
            panic!("Input vectors must have the same length");
        }
        let dot_product = linear(x, y);
        (dot_product + c).powi(d)
    }

    pub fn gaussian(x: &[f64], y: &[f64], sigma: f64) -> f64 {
        if x.len() != y.len() {
            panic!("Input vectors must have the same length");
        }
        let distance_squared: f64 = x.iter().zip(y.iter())
            .map(|(xi, yi)| (xi - yi).powi(2))
            .sum();
        (-distance_squared / (2.0 * sigma.powi(2))).exp()
    }

    pub fn sigmoid(x: &[f64], y: &[f64], alpha: f64, c: f64) -> f64 {
        if x.len() != y.len() {
            panic!("Input vectors must have the same length");
        }
        let dot_product = linear(x, y);
        (alpha * dot_product + c).tanh()
    }
}

With these kernel functions implemented, we can now apply them to a classification task. For instance, we could use a Support Vector Machine (SVM) classifier, which inherently relies on kernel functions for its operation. To compare the performance of different kernels, we can create a function that evaluates a dataset using each kernel and measures the accuracy of the classifications.

For simplicity, let’s assume we have a dataset represented as a vector of feature vectors and corresponding labels. The following code snippet demonstrates how to implement a basic classification routine using the SVM algorithm and our defined kernel functions.

mod kernels;

fn classify_with_kernel<F>(data: &[(Vec<f64>, i32)], kernel: F) -> f64
where
    F: Fn(&[f64], &[f64]) -> f64,
{
    // Simulate a simple SVM-like classification process
    let mut correct_predictions = 0;
    let total_samples = data.len();

    // Heuristic to compute predictions based on kernel similarities
    for i in 0..total_samples {
        let (x_i, label_i) = &data[i];

        // Accumulate a simple decision score for the current sample
        let mut decision_score = 0.0;

        for j in 0..total_samples {
            if i != j {
                let (x_j, label_j) = &data[j];
                let similarity = kernel(x_i, x_j);
                // Simplistic contribution to decision score
                decision_score += similarity * (*label_j as f64);
            }
        }

        // Make a prediction based on decision score
        let predicted_label = if decision_score >= 0.0 { 1 } else { -1 };

        if predicted_label == *label_i {
            correct_predictions += 1;
        }
    }

    correct_predictions as f64 / total_samples as f64
}

In this demonstration, the classify_with_kernel function takes a dataset and a kernel function, then calculates the number of correct predictions based on the kernel's output. It is essential to mention that this is a simplified representation and does not implement the complete SVM algorithm. However, it serves to illustrate how kernel functions can be integrated into classification tasks.

In conclusion, kernel functions play a vital role in machine learning models, particularly in dealing with non-linear data. Each kernel function comes with its distinct mathematical properties, advantages, and disadvantages. The choice of kernel can significantly impact the performance of the model, and understanding these nuances is crucial for effective machine learning practice. By implementing various kernels in Rust, we can leverage their strengths in classification tasks, allowing for a more versatile approach to solving complex problems in machine learning.

15.3. Support Vector Machines (SVMs) with Kernels link

Support Vector Machines (SVMs) are a powerful class of supervised learning algorithms used for both classification and regression tasks. They are particularly effective in situations where the goal is to find a hyperplane that optimally separates data points of different classes in a high-dimensional space. The central concept of SVMs is to identify the hyperplane that maximizes the margin between the closest points of different classes, known as support vectors. The margin is the distance between the hyperplane and the nearest data points from each class. By maximizing this margin, SVMs aim to find a decision boundary that generalizes well to unseen data.

Formally, consider a binary classification problem where the goal is to separate two classes of data points $\{x_i, y_i\}$, where $x_i \in \mathbb{R}^n$ represents the feature vector of the $i$-th data point and $y_i \in \{-1, 1\}$ represents the class label. A hyperplane in an nnn-dimensional space can be defined as:

$$ w^T x + b = 0, $$

where $w \in \mathbb{R}^n$ is the weight vector, and $b \in \mathbb{R}$ is the bias term. The decision function that determines the class of a new data point $x$ is given by:

$$f(x) = \text{sign}(w^T x + b).$$

The optimal hyperplane is the one that maximizes the margin between the two classes. For linearly separable data, this margin is defined as the distance between the hyperplane and the nearest data points from each class. These points are known as support vectors. The objective is to find $w$ and $b$ that maximize the margin, subject to the constraint that all data points are correctly classified. This can be formulated as a convex optimization problem:

$$\min_{w, b} \frac{1}{2} \|w\|^2,w,$$

subject to the constraints:

$$ y_i (w^T x_i + b) \geq 1, \quad \forall i = 1, \dots, N, $$

where $N$ is the number of training samples. The constraint $y_i (w^T x_i + b) \geq 1$ ensures that each data point is correctly classified with a margin of at least 1. The optimization problem seeks to minimize $|w\|^2$, which is equivalent to maximizing the margin, subject to the correct classification of the training data.

However, in many real-world scenarios, the data is not linearly separable in the original feature space. In such cases, the concept of soft margins is introduced, allowing for some misclassification in the training data. This leads to the formulation of the soft-margin SVM, where a penalty term is added to the objective function to account for misclassified points. The optimization problem for soft-margin SVMs becomes:

$$ \min_{w, b, \xi} \frac{1}{2} \|w\|^2 + C \sum_{i=1}^N \xi_i,w,b, $$

subject to the constraints:

$$ y_i (w^T x_i + b) \geq 1 - \xi_i, \quad \xi_i \geq 0, \quad \forall i = 1, \dots, N, $$

where $xi_i$ are slack variables that measure the degree of misclassification for each data point, and $C$ is a regularization parameter that controls the trade-off between maximizing the margin and minimizing the classification error. A larger value of $C$ penalizes misclassifications more heavily, while a smaller $C$ allows for a wider margin with more tolerance for misclassified points.

When the data is not linearly separable even with soft margins, kernel functions are introduced to extend SVMs to non-linear classification problems. The kernel trick is a mathematical technique that allows SVMs to operate in a higher-dimensional space without explicitly computing the transformation of the input data. Instead of mapping the data into a high-dimensional feature space $\mathcal{F}$, we define a kernel function $K(x_i, x_j)$ that computes the inner product in $\mathcal{F}$ directly:

$$ K(x_i, x_j) = \langle \phi(x_i), \phi(x_j) \rangle, $$

where $\phi(x)$ is the feature mapping that transforms the input data into the higher-dimensional space. By using the kernel function, we can solve the optimization problem in the original input space while implicitly operating in the high-dimensional feature space.

The choice of kernel function significantly affects the performance of the SVM, as different kernels induce different decision boundaries in the transformed feature space. Selecting the appropriate kernel requires understanding the underlying structure of the data and the complexity of the decision boundary. For example, if the data is linearly separable or nearly linear, the linear kernel may suffice. For more complex, non-linear relationships, the polynomial or RBF kernel is typically more effective.

In summary, Support Vector Machines (SVMs) are a powerful class of supervised learning algorithms that work by finding the hyperplane that maximizes the margin between different classes. In cases where the data is not linearly separable, the kernel trick allows SVMs to operate in a higher-dimensional space by implicitly transforming the data through kernel functions. The choice of kernel function, such as the polynomial, RBF, or sigmoid kernel, plays a critical role in the success of the SVM, as it determines the nature of the decision boundary and the model’s ability to generalize to unseen data.

In Rust, we can implement SVMs with various kernel functions to demonstrate their effectiveness in handling non-linear separability. To achieve this, we first need to define our kernel functions. The RBF kernel is particularly popular due to its localized nature, making it suitable for many real-world datasets.

Below is a sample Rust implementation of an SVM with an RBF kernel. We will create a struct to represent the SVM model, define methods for training the model, and implement the RBF kernel function.

use linfa; // A machine learning crate for Rust
use linfa::prelude::*;
use linfa_svm::{Svm, SvmParams};
use linfa_datasets::iris;

fn rbf_kernel(x: &Vec<f64>, y: &Vec<f64>, gamma: f64) -> f64 {
    let diff: Vec<f64> = x.iter().zip(y.iter()).map(|(a, b)| a - b).collect();
    let squared_distance = diff.iter().map(|d| d * d).sum::<f64>();
    (-gamma * squared_distance).exp()
}

fn main() {
    // Load the Iris dataset
    let dataset = iris::load();

    // Split the dataset into features and targets
    let (features, targets) = dataset.into_parts();

    // Define the SVM model with an RBF kernel
    let params = SvmParams::new().with_kernel(linfa_svm::Kernel::Custom(Box::new(|x, y| rbf_kernel(x, y, 0.1))));
    let model = Svm::fit(&params, &features, &targets).unwrap();

    // Make predictions
    let predictions = model.predict(&features);
    println!("{:?}", predictions);
}

In this implementation, we define a custom kernel function rbf_kernel that computes the RBF kernel value between two vectors. We then create an SVM model using the linfa_svm crate, which provides a convenient interface for training SVMs in Rust. We utilize the Iris dataset for training and evaluation. The fit method trains the SVM model, while the predict method generates predictions based on the training data.

Visualizing the decision boundaries of our trained SVM can provide valuable insights into its performance. To visualize the results, we can create a grid of points in the feature space and evaluate the model at those points. Below is an extension of the previous code that includes visualization using the plotters crate.

use plotters;
use plotters::prelude::*;

fn visualize_decision_boundary(model: &Svm<f64>, features: &Array2<f64>, targets: &Array1<f64>) {
    let root = BitMapBackend::new("decision_boundary.png", (640, 480)).into_drawing_area();
    root.fill(&WHITE).unwrap();

    let mut chart = ChartBuilder::on(&root)
        .caption("SVM Decision Boundary", ("sans-serif", 50).into_font())
        .margin(5)
        .x_label_area_size(30)
        .y_label_area_size(30)
        .build_cartesian_2d(-5.0..5.0, -5.0..5.0)
        .unwrap();

    chart.configure_series_labels().border_style(&BLACK).draw().unwrap();

    // Plot the decision boundary
    for x in -5..5 {
        for y in -5..5 {
            let point = vec![x as f64, y as f64];
            let pred = model.predict(&Array2::from_shape_vec((1, 2), point).unwrap());
            if pred[0] == 1.0 {
                chart.draw_series(PointSeries::of_element(vec![(x as f64, y as f64)], 5, &RED, &circle))
                    .unwrap();
            } else {
                chart.draw_series(PointSeries::of_element(vec![(x as f64, y as f64)], 5, &BLUE, &circle))
                    .unwrap();
            }
        }
    }

    // Plot the original data points
    for (i, target) in targets.iter().enumerate() {
        let point = features.row(i);
        let color = if *target == 1.0 { &RED } else { &BLUE };
        chart.draw_series(PointSeries::of_element(vec![(point[0], point[1])], 5, color, &circle)).unwrap();
    }
}

fn main() {
    let dataset = iris::load();
    let (features, targets) = dataset.into_parts();
    let params = SvmParams::new().with_kernel(linfa_svm::Kernel::Custom(Box::new(|x, y| rbf_kernel(x, y, 0.1))));
    let model = Svm::fit(&params, &features, &targets).unwrap();
    
    visualize_decision_boundary(&model, &features, &targets);
}

In this enhanced code, we introduce a visualize_decision_boundary function that creates a plot of the SVM decision boundary along with the original data points. The decision boundary is represented in red and blue colors corresponding to the two classes. The function iterates over a grid of points, predicts their class using the trained model, and draws the points accordingly.

In conclusion, Support Vector Machines, when combined with kernel functions, offer a robust approach to tackle non-linear classification problems. By leveraging the kernel trick, we can efficiently operate in higher-dimensional spaces without explicitly transforming our data. The Rust implementation provided demonstrates how to define kernel functions, train an SVM model, and visualize the resulting decision boundaries, offering a comprehensive understanding of the capabilities of SVMs in machine learning. As we continue to explore various kernel methods and SVM configurations, it becomes clear that these techniques are invaluable tools for solving complex classification tasks in diverse domains.

15.4. Kernel Principal Component Analysis (KPCA) link

Kernel Principal Component Analysis (KPCA) is a sophisticated extension of the conventional Principal Component Analysis (PCA), designed to capture non-linear relationships in the data by utilizing kernel methods. While PCA excels at identifying linear structures, it falls short in handling complex, non-linear patterns that frequently arise in real-world datasets. KPCA overcomes this limitation by projecting the data into a higher-dimensional feature space through a kernel function, allowing it to uncover non-linear structures that PCA cannot capture. The central innovation of KPCA is the use of the kernel trick, which enables it to compute inner products in the high-dimensional space without explicitly performing the transformation, making the approach computationally feasible.

To fully appreciate KPCA, it is important to first recall the mathematical foundations of traditional PCA. In PCA, the goal is to reduce the dimensionality of the data by identifying the directions (principal components) that capture the most variance. This is achieved by computing the eigenvectors and eigenvalues of the covariance matrix $C$, where $C$ is defined as:

$$ C = \frac{1}{N} \sum_{i=1}^{N} (x_i - \bar{x})(x_i - \bar{x})^T, $$

with $x_i \in \mathbb{R}^d$ representing the iii-th data point, $\bar{x}$ the mean of the data, and $N$ the number of data points. The principal components correspond to the eigenvectors of the covariance matrix, and their associated eigenvalues indicate the amount of variance captured by each component. By projecting the data onto the principal components associated with the largest eigenvalues, PCA effectively reduces the dimensionality of the dataset while preserving as much information as possible.

However, PCA operates in the original feature space and assumes linear relationships between the variables, which limits its ability to capture non-linear patterns. This is where KPCA proves invaluable. The core idea of KPCA is to map the input data into a higher-dimensional feature space $\mathcal{F}$ through a non-linear function $\phi: \mathbb{R}^d \to \mathcal{F}$. In this transformed space, the data may exhibit linear separability, allowing KPCA to extract meaningful principal components that reflect non-linear structures in the original data. Mathematically, the transformation $\phi(x)$ takes the input data $x \in \mathbb{R}^d$ and maps it into the higher-dimensional space $\mathcal{F}$, where the inner product between any two data points $x_i$ and $x_j$ is given by a kernel function $k(x_i, x_j)$:

$$ k(x_i, x_j) = \langle \phi(x_i), \phi(x_j) \rangle_{\mathcal{F}}. $$

The kernel function $k(x_i, x_j)$ computes the inner product in the feature space $\mathcal{F}$ without the need to explicitly compute the mapping $\phi(x)$, a technique known as the kernel trick. This allows KPCA to avoid the computational burden of directly working in the high-dimensional space, which would often be intractable due to the curse of dimensionality.

To perform KPCA, we begin by constructing the kernel matrix $K$, where each element $K_{ij} = k(x_i, x_j)$ represents the similarity between data points $x_i$ and $x_j$ in the transformed feature space. The kernel matrix $K$ is analogous to the covariance matrix in traditional PCA, and its eigenvectors and eigenvalues are used to compute the principal components in the feature space. Specifically, the kernel matrix $K$ is centered to remove the effect of the mean, ensuring that the data is zero-centered in the transformed space. The centered kernel matrix $\tilde{K}$ is computed as:

$$ \tilde{K} = K - \mathbf{1}_N K - K \mathbf{1}_N + \mathbf{1}_N K \mathbf{1}_N, $$

where $\mathbf{1}_N$ is an $N \times N$ matrix with all entries equal to $\frac{1}{N}$. This centering step is necessary to ensure that the kernel PCA operates in a zero-mean feature space, as in traditional PCA.

Next, we compute the eigenvectors α\\alphaα and eigenvalues λ\\lambdaλ of the centered kernel matrix $\tilde{K}$:

$$ \tilde{K} \alpha = \lambda \alpha. $$

The eigenvectors $\alpha_i$ corresponding to the largest eigenvalues $\lambda_i$ represent the principal components in the feature space. These eigenvectors are then used to project the original data into the principal component space, effectively reducing the dimensionality of the data while preserving the non-linear structures.

To project a new data point $x$ into the principal component space, we compute the projection using the kernel function:

$$ z_i = \sum_{j=1}^{N} \alpha_{ij} k(x_j, x), $$

where $z_i$ represents the projection onto the $i$-th principal component. This process allows us to reduce the dimensionality of new data points in the same way that traditional PCA reduces dimensionality for linear data.

The choice of kernel function plays a crucial role in determining the success of KPCA. Common kernel functions include the polynomial kernel, radial basis function (RBF) kernel, and sigmoid kernel. Each kernel function defines a different similarity measure in the transformed feature space, and the appropriate choice depends on the nature of the data. The polynomial kernel, defined as:

$$ k(x_i, x_j) = (x_i^T x_j + c)^d, $$

is useful when the data exhibits polynomial-like relationships. The RBF kernel, defined as:

$$ k(x_i, x_j) = \exp\left(-\frac{\|x_i - x_j\|^2}{2 \sigma^2}\right), $$

is particularly effective for capturing complex, non-linear relationships and is widely used in KPCA for its flexibility. The sigmoid kernel, defined as:

$$ k(x_i, x_j) = \tanh(\alpha x_i^T x_j + c), $$

is related to neural networks and can capture certain types of non-linear relationships, though it is less commonly used compared to the polynomial and RBF kernels.

In conclusion, Kernel Principal Component Analysis (KPCA) extends the conventional PCA to handle non-linear relationships by leveraging the kernel trick. By mapping the data into a higher-dimensional feature space and computing principal components in this transformed space, KPCA can detect intricate data patterns that are inaccessible to linear methods. The choice of kernel function is critical, as it defines the nature of the transformation and the similarity measure in the feature space. Through its ability to capture non-linear structures, KPCA provides a powerful tool for dimensionality reduction in complex datasets, making it highly applicable in a wide range of machine learning tasks.

Implementing KPCA in Rust involves several key steps, including defining a suitable kernel function, constructing the kernel matrix, centering it, and then performing the eigenvalue decomposition. The following sample code illustrates how to implement KPCA using the Gaussian (RBF) kernel, a popular choice due to its ability to handle non-linear relationships effectively.

use nalgebra as na;
use na::{DMatrix, DVector, SymmetricEigen};

fn gaussian_kernel(x: &DVector<f64>, y: &DVector<f64>, sigma: f64) -> f64 {
    let diff = x - y;
    let norm = diff.norm_squared();
    (-norm / (2.0 * sigma * sigma)).exp()
}

fn compute_kernel_matrix(data: &DMatrix<f64>, sigma: f64) -> DMatrix<f64> {
    let num_samples = data.nrows();
    let mut kernel_matrix = DMatrix::zeros(num_samples, num_samples);

    for i in 0..num_samples {
        for j in 0..num_samples {
            let x_i = data.row(i).transpose();
            let x_j = data.row(j).transpose();
            kernel_matrix[(i, j)] = gaussian_kernel(&x_i, &x_j, sigma);
        }
    }

    kernel_matrix
}

fn center_kernel_matrix(kernel_matrix: &DMatrix<f64>) -> DMatrix<f64> {
    let n = kernel_matrix.nrows() as f64;
    let row_means = kernel_matrix.row_sum() / n;
    let col_means = kernel_matrix.column_sum() / n;
    let total_mean = kernel_matrix.sum() / (n * n);

    let mut centered = kernel_matrix.clone();
    for i in 0..kernel_matrix.nrows() {
        for j in 0..kernel_matrix.ncols() {
            centered[(i, j)] = kernel_matrix[(i, j)] - row_means[i] - col_means[j] + total_mean;
        }
    }
    centered
}

fn kpca(data: &DMatrix<f64>, sigma: f64, num_components: usize) -> (DMatrix<f64>, DVector<f64>) {
    let kernel_matrix = compute_kernel_matrix(data, sigma);
    let centered_kernel_matrix = center_kernel_matrix(&kernel_matrix);

    let eigen = SymmetricEigen::new(centered_kernel_matrix);
    let eigenvalues = eigen.eigenvalues;
    let eigenvectors = eigen.eigenvectors;

    // Sort eigenvalues and corresponding eigenvectors in descending order
    let mut indices: Vec<usize> = (0..eigenvalues.len()).collect();
    indices.sort_unstable_by(|&i, &j| eigenvalues[j].partial_cmp(&eigenvalues[i]).unwrap());

    let mut principal_components = DMatrix::zeros(data.nrows(), num_components);
    let mut variances = DVector::zeros(num_components);

    for (i, &index) in indices.iter().enumerate().take(num_components) {
        variances[i] = eigenvalues[index];
        principal_components.set_column(i, &eigenvectors.column(index));
    }

    (principal_components, variances)
}

fn main() {
    // Example usage
    let data = DMatrix::from_row_slice(5, 2, &[
        1.0, 2.0,
        2.0, 3.0,
        3.0, 3.0,
        4.0, 5.0,
        5.0, 6.0,
    ]);

    let sigma = 1.0; // Bandwidth for Gaussian kernel
    let num_components = 2;

    let (principal_components, variances) = kpca(&data, sigma, num_components);

    println!("Principal Components:\n{}", principal_components);
    println!("Variances:\n{}", variances);
}

In this implementation, we define a Gaussian kernel function that computes the similarity between two data points. The compute_kernel_matrix function constructs the kernel matrix, followed by centering it with center_kernel_matrix. The kpca function orchestrates the overall process, performing eigenvalue decomposition to extract the principal components and their corresponding variances.

When applying KPCA to datasets with non-linear structures, one can observe significant differences in the results compared to standard PCA. For example, if we were to visualize the results of KPCA applied to a spiral dataset, we would see that KPCA is capable of unfolding the spiral into a linear representation, enabling effective separation of classes that PCA would struggle with.

In conclusion, KPCA provides a robust framework for dimensionality reduction in the presence of non-linear relationships within data. By utilizing kernel functions to project data into a higher-dimensional space, KPCA captures complex structures that traditional PCA cannot. The implementation in Rust showcases the potential of leveraging efficient data structures to perform KPCA, making it a valuable tool for machine learning practitioners focusing on non-linear problems.

15.5. Gaussian Processes and Kernels link

Gaussian Processes (GPs) have gained significant attention in machine learning due to their flexibility and powerful probabilistic framework for both regression and classification tasks. Unlike parametric models, which assume a fixed form for the underlying function (with a predetermined number of parameters), GPs adopt a non-parametric approach, allowing the model to adapt its complexity according to the observed data. The foundational concept behind GPs lies in the idea of defining a distribution over functions, where any finite set of points follows a joint Gaussian distribution. This provides a robust mechanism for capturing uncertainty in predictions, which is one of the primary strengths of Gaussian Processes.

A Gaussian Process is defined as a collection of random variables, any finite number of which have a joint Gaussian distribution. Formally, a GP is written as:

$$ f(x) \sim \mathcal{GP}(m(x), k(x, x')), $$

where $m(x)$ is the mean function, and $k(x, x')$ is the covariance function or kernel. The mean function $m(x)$ specifies the expected value of the function at any input point $x$, while the kernel function $k(x, x')$ describes the covariance between function values at any two input points $x$ and $x'$. In practice, the mean function is often assumed to be zero for simplicity, especially in regression tasks where the focus is on modeling the deviation from the mean rather than the mean itself. The kernel function, however, plays a crucial role in capturing the smoothness, periodicity, and other properties of the underlying function.

The choice of the kernel function is central to Gaussian Processes. The kernel encodes prior knowledge about the structure of the function, such as smoothness, periodicity, or stationarity, and it defines the covariance matrix that governs the correlations between different points in the input space. For example, the squared exponential (Gaussian) kernel, defined as:

$$ k(x, x') = \exp\left( -\frac{\|x - x'\|^2}{2 \sigma^2} \right), $$

is a popular choice for many applications because it assumes that the function is smooth, with nearby points in the input space having highly correlated function values. The parameter σ\\sigmaσ controls the length scale, determining how quickly the correlation decays as the distance between two points increases. Other kernel functions, such as the Matérn kernel or the periodic kernel, can be used to capture different types of structures in the data.

To understand the mechanics of a Gaussian Process, consider a set of training inputs $X = \{x_1, x_2, ..., x_n\}$ and their corresponding observed outputs $y = \{y_1, y_2, ..., y_n\}$. The key idea is that the function values $f(X) = \{f(x_1), f(x_2), ..., f(x_n)\}$ are jointly distributed as a multivariate Gaussian distribution:

$$ f(X) \sim \mathcal{N}(m(X), K(X, X)), $$

where $m(X)$ is the mean vector, and $K(X, X)$ is the covariance matrix, with $K_{ij} = k(x_i, x_j)$. Given this structure, Gaussian Processes model the distribution over functions, allowing us to make predictions at new input points by conditioning on the observed data.

In regression tasks, the goal is to predict the value of the function $f(x_*)$ at a new input point $x_*$ given the training data $X$ and the observed outputs $y$. The predictive distribution for $f(x_*)$ is Gaussian, with the mean $\mu_<*$ and variance $\sigma_*^2$ given by:

$$ \mu_* = k(x_*, X) K(X, X)^{-1} y, $$

$$ \sigma_*^2 = k(x_*, x_*) - k(x_*, X) K(X, X)^{-1} k(X, x_*). $$

Here, $k(x_*, X)$ represents the vector of covariances between the test point $x_*$ and the training points, and $K(X, X)$ is the covariance matrix of the training points. The term $k(x_*, x_*)$ is the variance at the new point $x_*$, and the difference $k(x_*, x_*) - k(x_*, X) K(X, X)^{-1} k(X, x_*)$ quantifies the uncertainty in the prediction. This structure allows GPs to provide not only a point estimate of the prediction (the mean $\mu_*$) but also a measure of uncertainty (the variance $\sigma_*^2$).

Gaussian Processes offer several advantages in machine learning tasks. First, their non-parametric nature allows them to model complex functions without the need for explicit parameter tuning or selecting a fixed model structure. The flexibility of GPs means that they can adapt their complexity based on the observed data. Second, GPs provide a natural way to incorporate prior knowledge about the function being modeled through the choice of the kernel. For instance, if we believe the function is smooth, we can choose a kernel like the squared exponential kernel that enforces this property. Finally, GPs give probabilistic predictions, which means that they not only predict the mean of the function but also the uncertainty associated with that prediction. This is particularly useful in applications where it is important to quantify the uncertainty in the model’s predictions.

However, Gaussian Processes also come with computational challenges. The most significant of these is the inversion of the covariance matrix $K(X, X)$, which has a computational complexity of $O(n^3)$, where $n$ is the number of training points. This can make GPs computationally expensive for large datasets. Several approximation techniques, such as sparse Gaussian Processes or inducing point methods, have been developed to address this limitation, allowing GPs to scale to larger datasets while maintaining their probabilistic nature.

In practical terms, implementing Gaussian Processes in Rust involves constructing the kernel matrix KKK based on the chosen kernel function, computing the predictive mean and variance, and ensuring numerical stability when inverting the covariance matrix. Rust’s strong performance characteristics and concurrency support make it a suitable language for implementing GPs, especially for large-scale applications where efficiency is paramount.

In conclusion, Gaussian Processes provide a powerful, flexible framework for regression and classification tasks, offering both accurate predictions and uncertainty quantification. Their reliance on kernel functions allows them to model complex relationships in the data, making them a valuable tool in many machine learning applications. The ability to incorporate prior knowledge and provide probabilistic predictions sets GPs apart from other machine learning models, although their computational cost must be carefully managed in practice. Through careful kernel selection and efficient implementation, Gaussian Processes can be effectively applied to a wide range of machine learning problems.

In Rust, implementing Gaussian Processes involves utilizing libraries for matrix operations, as well as defining various kernels to model different types of data. Below is an example of how one might implement the RBF kernel in Rust:

use nalgebra as na;

fn rbf_kernel(x: &na::Vector2<f64>, y: &na::Vector2<f64>, length_scale: f64, variance: f64) -> f64 {
    let squared_distance = (x - y).norm_squared();
    variance * (-squared_distance / (2.0 * length_scale.powi(2))).exp()
}

In this example, we have defined a function rbf_kernel that computes the RBF kernel between two 2-dimensional vectors. Utilizing the nalgebra crate allows for efficient vector operations, essential for calculating the covariance matrix in a Gaussian Process.

To implement Gaussian Processes for regression tasks, we will need to create the covariance matrix and make predictions based on the training data. Below is a simplified version of how one might structure this in Rust, integrating the kernel function defined previously:

use nalgebra as na;
use na::{DMatrix, DVector};

struct GaussianProcess {
    length_scale: f64,
    variance: f64,
    train_x: Vec<na::Vector2<f64>>,
    train_y: DVector<f64>,
    cov_matrix: DMatrix<f64>,
}

impl GaussianProcess {
    fn new(length_scale: f64, variance: f64) -> Self {
        Self {
            length_scale,
            variance,
            train_x: Vec::new(),
            train_y: DVector::zeros(0),
            cov_matrix: DMatrix::zeros(0, 0),
        }
    }

    fn fit(&mut self, x: Vec<na::Vector2<f64>>, y: Vec<f64>) {
        self.train_x = x;
        self.train_y = DVector::from_vec(y);
        let n = self.train_x.len();
        self.cov_matrix = DMatrix::zeros(n, n);

        for i in 0..n {
            for j in 0..n {
                self.cov_matrix[(i, j)] = rbf_kernel(&self.train_x[i], &self.train_x[j], self.length_scale, self.variance);
            }
        }

        // Add jitter for numerical stability
        let jitter = 1e-6;
        for i in 0..n {
            self.cov_matrix[(i, i)] += jitter;
        }
    }

    fn predict(&self, x_star: &na::Vector2<f64>) -> (f64, f64) {
        let k_star = DVector::from_iterator(self.train_x.len(), self.train_x.iter()
            .map(|x| rbf_kernel(x_star, x, self.length_scale, self.variance)));

        let k_star_star = rbf_kernel(x_star, x_star, self.length_scale, self.variance);

        // Invert the covariance matrix (note: this may fail if the matrix is not positive definite)
        let k_inv = self.cov_matrix.clone().try_inverse().unwrap();

        // Calculate the mean prediction
        let mu_star = k_star.transpose() * &k_inv * &self.train_y;

        // Calculate the variance prediction
        let variance_star = k_star_star - (k_star.transpose() * &k_inv * &k_star)[(0, 0)];

        (mu_star[(0, 0)], variance_star)
    }
}

fn rbf_kernel(x: &na::Vector2<f64>, y: &na::Vector2<f64>, length_scale: f64, variance: f64) -> f64 {
    let squared_distance = (x - y).norm_squared();
    variance * (-squared_distance / (2.0 * length_scale.powi(2))).exp()
}

fn main() {
    // Example usage
    let train_x = vec![
        na::Vector2::new(1.0, 2.0),
        na::Vector2::new(3.0, 4.0),
        na::Vector2::new(5.0, 6.0),
    ];
    let train_y = vec![1.0, 2.0, 3.0];

    let mut gp = GaussianProcess::new(1.0, 1.0);
    gp.fit(train_x, train_y);

    let x_star = na::Vector2::new(4.0, 5.0);
    let (mean, variance) = gp.predict(&x_star);

    println!("Predicted mean: {}", mean);
    println!("Predicted variance: {}", variance);
}

In this implementation, we define a GaussianProcess struct that holds the length scale, variance, training data, and the covariance matrix. The fit method computes the covariance matrix based on the training data using the RBF kernel. The predict method computes the mean and variance for a new input point \\( x\_\* \\), allowing us to make predictions based on the learned process.

In conclusion, Gaussian Processes combined with kernel methods provide a robust framework for modeling complex data distributions in a flexible manner. By defining appropriate kernels, we can capture various properties of the underlying function we wish to learn, and Rust's strong type system and performance characteristics make it an excellent choice for implementing such probabilistic models. As we continue to explore the capabilities of Gaussian Processes, we can experiment with different kernels, hyperparameter tuning, and even extensions to multi-dimensional data.

15.6. Multiple Kernel Learning link

Multiple Kernel Learning (MKL) is a powerful and flexible technique in machine learning that leverages the use of multiple kernel functions to improve model performance in complex data environments. The key idea behind MKL is to construct a model that integrates various kernels, each designed to capture different aspects of the data, thereby enhancing the model’s ability to generalize across diverse patterns. In contrast to using a single kernel, which might only capture specific relationships (such as linear or non-linear), MKL allows for a combination of kernels, each contributing to different facets of the data structure. This versatility makes MKL particularly effective in scenarios where the data exhibits multiple underlying patterns or relationships that a single kernel would fail to capture fully.

The mathematical formulation of MKL is based on the notion of combining a set of base kernels. Let $K_1(x, x'), K_2(x, x'), \dots, K_m(x, x')$ represent the individual kernel functions, each defining a different similarity measure between two data points $x$ and $x'$. The goal of MKL is to find an optimal combination of these kernels that best models the data. This is achieved by learning a linear combination of the base kernels:

$$ K_{\text{MKL}}(x, x') = \sum_{i=1}^m \beta_i K_i(x, x'), $$

where $\beta_i$ are non-negative weights associated with each kernel $K_i$, and $m$ is the total number of kernels. The weights $\beta_i$ control the contribution of each kernel to the overall model, and they are learned as part of the optimization process. The objective is to find the weights that minimize the loss function while maintaining a balance between model complexity and the ability to fit the data.

In the context of supervised learning, MKL is typically framed as an optimization problem where the goal is to minimize a regularized empirical risk function. The standard formulation involves minimizing a loss function $L(y, f(x))$, where $y$ represents the true labels, $f(x)$ is the model's prediction, and $L$ is a loss function, such as the hinge loss for classification tasks. The MKL optimization problem can be expressed as:

$$ \min_{f, \beta} \frac{1}{n} \sum_{i=1}^n L(y_i, f(x_i)) + \lambda \sum_{i=1}^m \|\beta_i\|_p,f, $$

where $n$ is the number of training samples, $\lambda$ is a regularization parameter, and the second term represents a regularizer applied to the kernel weights $\beta_i$ to prevent overfitting. The regularization norm $p$ controls the sparsity of the kernel weights, encouraging the model to focus on a subset of the most relevant kernels. For example, if $p = 1$, the regularization promotes sparsity in the kernel weights, meaning that only a few kernels will have non-zero weights. This helps reduce overfitting by preventing the model from relying too heavily on a large number of kernels.

The kernel functions $K_i(x, x')$ in MKL are selected based on the specific properties they capture. For instance, a linear kernel:

$$ K_{\text{linear}}(x, x') = x^T x', $$

captures linear relationships in the data, while the radial basis function (RBF) kernel:

$$ K_{\text{RBF}}(x, x') = \exp\left(-\frac{\|x - x'\|^2}{2 \sigma^2}\right), $$

captures non-linear relationships by mapping the data into an infinite-dimensional space. Other kernels, such as polynomial kernels or sigmoid kernels, can also be included depending on the nature of the data and the problem being solved.

One of the critical challenges in MKL is selecting the appropriate set of kernels and determining their optimal combination. If the kernels are not chosen carefully, the model may underfit or overfit the data. Overfitting occurs when the model becomes too complex by combining too many kernels without sufficient regularization. This results in a model that fits the training data well but performs poorly on unseen data due to its inability to generalize. To mitigate this issue, careful regularization is applied to the kernel weights, and cross-validation is often used to tune the regularization parameter λ\\lambdaλ and select the most effective kernels.

The advantage of MKL lies in its ability to capture multiple aspects of the data simultaneously. For example, in image classification tasks, different kernels may focus on different characteristics of the images: one kernel might be particularly effective at capturing texture, while another might focus on shape or color. By combining these kernels, MKL can form a more complete and nuanced understanding of the data, leading to improved classification accuracy and robustness.

The optimization process in MKL involves both finding the model parameters and learning the kernel weights βi\\beta_iβi. This requires solving a more complex optimization problem compared to single-kernel methods, and as such, it can be computationally demanding. However, various algorithms, such as semi-infinite programming, gradient-based methods, or block-coordinate descent, have been developed to efficiently solve MKL problems, making it feasible for large-scale applications.

In terms of implementation, Rust’s efficiency and concurrency features make it well-suited for developing MKL algorithms, especially when handling large datasets or combining multiple kernels. The ability to parallelize kernel matrix computations and optimize the model’s parameters efficiently is crucial for scaling MKL to practical machine learning tasks.

In conclusion, Multiple Kernel Learning (MKL) is a robust technique that enhances the performance of machine learning models by combining multiple kernels to capture different aspects of the data. By learning a weighted combination of kernels, MKL can adapt to complex datasets where a single kernel may not be sufficient. The optimization of kernel weights and model parameters requires careful regularization to balance model complexity and avoid overfitting. While MKL can be computationally intensive, its ability to provide flexible and accurate models makes it a valuable tool in modern machine learning applications.

To implement Multiple Kernel Learning in Rust, one would begin by defining the necessary kernels. For demonstration purposes, let's consider a simple scenario where we have two kernels: a linear kernel and a radial basis function (RBF) kernel. The following Rust code snippet illustrates how to define these kernels and implement a basic MKL framework.

use nalgebra as na;
use na::{DMatrix, DVector};

// Define a trait for kernel operations
trait Kernel {
    fn compute(&self, x1: &DVector<f64>, x2: &DVector<f64>) -> f64;
}

// Linear Kernel Implementation
struct LinearKernel;

impl Kernel for LinearKernel {
    fn compute(&self, x1: &DVector<f64>, x2: &DVector<f64>) -> f64 {
        x1.dot(x2)
    }
}

// RBF Kernel Implementation
struct RBFKernel {
    gamma: f64,
}

impl Kernel for RBFKernel {
    fn compute(&self, x1: &DVector<f64>, x2: &DVector<f64>) -> f64 {
        let diff = x1 - x2;
        (-self.gamma * diff.norm_squared()).exp()
    }
}

// Multiple Kernel Learning (MKL) Struct
struct MKL {
    kernels: Vec<Box<dyn Kernel>>,
    weights: Vec<f64>,
}

impl MKL {
    fn new(kernels: Vec<Box<dyn Kernel>>, weights: Vec<f64>) -> Self {
        MKL { kernels, weights }
    }

    fn compute_kernel_matrix(&self, data: &DMatrix<f64>) -> DMatrix<f64> {
        let n = data.nrows();
        let mut kernel_matrix = DMatrix::zeros(n, n);
        for i in 0..n {
            for j in 0..n {
                let mut sum = 0.0;
                let x_i = DVector::from_iterator(data.ncols(), data.row(i).iter().cloned());
                let x_j = DVector::from_iterator(data.ncols(), data.row(j).iter().cloned());
                for (kernel, weight) in self.kernels.iter().zip(&self.weights) {
                    sum += weight * kernel.compute(&x_i, &x_j);
                }
                kernel_matrix[(i, j)] = sum;
            }
        }
        kernel_matrix
    }

    // Add methods for training and prediction if needed
}

fn main() {
    // Define kernels
    let linear_kernel = LinearKernel {};
    let rbf_kernel = RBFKernel { gamma: 0.5 };

    // Create a vector of kernels
    let kernels: Vec<Box<dyn Kernel>> = vec![
        Box::new(linear_kernel),
        Box::new(rbf_kernel),
    ];

    let weights = vec![0.5, 0.5]; // Initial weights for kernels

    // Create an MKL instance
    let mkl = MKL::new(kernels, weights);

    // Define data as a DMatrix<f64>
    let data = DMatrix::from_row_slice(4, 2, &[1.0, 2.0, 2.0, 3.0, 3.0, 4.0, 4.0, 5.0]);

    // Compute the kernel matrix
    let kernel_matrix = mkl.compute_kernel_matrix(&data);
    println!("Kernel Matrix:\n{}", kernel_matrix);
}

In this code snippet, we define two types of kernels: LinearKernel and RBFKernel. Each kernel has a compute method that calculates the kernel value between two input vectors. The MKL struct holds a vector of kernels and their associated weights. The compute_kernel_matrix method constructs a kernel matrix by iterating through the data points and combining the contributions from each kernel based on the specified weights.

As we build on this framework, additional methods for training the MKL model, such as optimization routines for adjusting the kernel weights and model parameters, can be incorporated. Furthermore, it is crucial to experiment with different sets of kernels and weights on complex datasets to evaluate the performance of the MKL approach against single kernel methods. This evaluation could involve using metrics such as accuracy, precision, recall, or F1-score, as well as cross-validation techniques to ensure that the model generalizes well to unseen data.

In conclusion, Multiple Kernel Learning represents a significant advancement in the field of machine learning, particularly when dealing with complex datasets characterized by heterogeneous features and structures. By effectively combining kernels, we can harness the distinct advantages of each and achieve superior model performance. The implementation in Rust not only offers the potential for high performance but also provides a robust framework for further exploration and experimentation in MKL methodologies.

15.7. Applications of Kernel Methods link

Kernel methods have emerged as a powerful tool in the field of machine learning, offering unique advantages across various domains such as bioinformatics, image processing, and natural language processing. They allow us to operate in high-dimensional spaces without the need for explicit transformations, enabling the kernel trick to be utilized effectively. The fundamental idea behind kernel methods lies in their ability to compute dot products in a transformed feature space without ever needing to calculate the coordinates of the data in that space. This capability makes them particularly suited for complex data distributions and non-linear relationships.

In bioinformatics, kernel methods are used extensively for tasks such as gene expression analysis, protein structure prediction, and the classification of biological sequences. For instance, Support Vector Machines (SVMs) with Gaussian kernels are often employed to classify gene expression data, where the relationship between different genes may not be linearly separable. By applying kernel methods, researchers can identify patterns and relationships among genes that contribute to specific diseases, leading to advancements in personalized medicine. Similarly, in image processing, kernel methods are utilized for image classification, segmentation, and object recognition. Convolutional kernels, which can be seen as a specific type of kernel method, allow for the extraction of features from images, enhancing the ability to classify and interpret visual data.

Natural language processing (NLP) is another domain where kernel methods shine. With the rise of large text corpora, the need for effective text classification algorithms has become paramount. Kernel methods can be used to create models that classify documents based on their content, utilizing various kernels such as the polynomial kernel or the string kernel, which captures similarities between sequences of characters. These applications can significantly improve tasks such as sentiment analysis, topic detection, and spam filtering.

The conceptual understanding of how kernel methods solve real-world problems lies in their flexibility and robustness. By mapping input data into high-dimensional spaces, kernel methods can uncover complex relationships that traditional linear models might miss. The kernel trick allows for computational efficiency, as it avoids the explicit transformation of data while still benefiting from the properties of the transformed space. This leads to improved generalization performance on unseen data, making kernel methods particularly appealing for tasks with limited training examples.

To illustrate the practical implementation of kernel methods, let's consider a simple text classification problem in Rust. We can use the ndarray and linfa libraries to create a kernel-based classifier. The following code snippet demonstrates how to implement a Support Vector Machine with a Gaussian kernel for text classification.

use linfa::prelude::*;
use linfa_svm::{Svm, Kernel};
use ndarray::Array2;

fn main() {
    // Sample data: representing two classes of text documents
    let features: Array2<f64> = Array2::from_shape_vec((6, 2), vec![
        1.0, 2.0,   // Class 1
        1.5, 1.8,   // Class 1
        5.0, 8.0,   // Class 2
        6.0, 9.0,   // Class 2
        1.0, 0.6,   // Class 1
        9.0, 11.0,  // Class 2
    ]).unwrap();
    
    let targets = vec![0, 0, 1, 1, 0, 1]; // Class labels

    // Create a dataset
    let dataset = Dataset::new(features, targets);

    // Train a Support Vector Machine with Gaussian kernel
    let model = Svm::params()
        .with_kernel(Kernel::Gaussian)
        .fit(&dataset)
        .expect("Failed to train SVM");

    // Test with a new data point
    let new_point = Array2::from_shape_vec((1, 2), vec![3.0, 5.0]).unwrap();
    let prediction = model.predict(&new_point);
    
    println!("Predicted class: {}", prediction);
}

In this example, we first create a dataset containing two classes of text documents represented as numerical feature vectors. After transforming our input data into a compatible format, we utilize the linfa_svm crate to construct a Support Vector Machine model with a Gaussian kernel. Once trained, we can make predictions on new data points, showcasing the practical application of kernel methods in a text classification task.

Evaluating the performance of such models can be achieved through cross-validation, confusion matrices, and metrics such as accuracy, precision, and recall. By applying kernel methods in real-world scenarios, we can observe the robustness and effectiveness of these techniques in handling complex datasets, ultimately leading to enhanced predictive capabilities.

In summary, kernel methods are invaluable across various fields due to their ability to handle non-linear relationships and high-dimensional data elegantly. Their applications in bioinformatics, image processing, and natural language processing demonstrate their versatility and effectiveness, while practical implementations in Rust provide a solid foundation for building advanced machine learning systems. By leveraging the power of kernel methods, we can address real-world challenges and unlock new insights from complex data.

15.8. Conclusion link

Chapter 15 equips you with a deep understanding of Kernel Methods and their implementation in Rust. By mastering these techniques, you will be able to tackle complex, non-linear problems in high-dimensional spaces, unlocking new possibilities in machine learning applications.

15.8.1. Further Learning with GenAI link

By exploring these questions, you will deepen your knowledge of the theoretical foundations, kernel function properties, and applications of Kernel Methods in various domains.

• Explain the fundamental concept of the kernel trick. How does the kernel trick enable algorithms to operate in high-dimensional spaces without explicitly computing the coordinates, and why is this important in machine learning? Implement a simple kernelized algorithm in Rust.

• Discuss the role of kernel functions in machine learning. How do kernel functions transform data into higher-dimensional spaces, and what are the key differences between linear and non-linear kernels? Implement and compare different kernel functions in Rust.

• Analyze the properties of the Gaussian (RBF) kernel. How does the Gaussian kernel measure similarity between data points, and in what scenarios is it most effective? Implement the Gaussian kernel in Rust and apply it to a classification task.

• Explore the use of polynomial kernels in SVMs. How do polynomial kernels map data into higher-dimensional spaces, and what are the trade-offs between polynomial degree and model complexity? Implement an SVM with a polynomial kernel in Rust and evaluate its performance on non-linear data.

• Discuss the concept of margin maximization in Support Vector Machines (SVMs). How do SVMs find the optimal hyperplane that maximizes the margin between classes, and how does the choice of kernel affect this process? Implement an SVM with different kernels in Rust and visualize the decision boundaries.

• Analyze the role of the kernel trick in Kernel Principal Component Analysis (KPCA). How does KPCA extend traditional PCA to capture non-linear structures in data, and what are the advantages of using KPCA over PCA? Implement KPCA in Rust and apply it to a dataset with non-linear patterns.

• Explore the use of Gaussian Processes (GPs) with kernels. How do kernels define the covariance functions in GPs, and how does this influence the behavior of the Gaussian process? Implement a GP in Rust using different kernel functions and apply it to a regression task.

• Discuss the challenges of kernel selection in machine learning. How does the choice of kernel function impact model performance, and what techniques can be used to select the optimal kernel? Implement a kernel selection process in Rust and evaluate its effectiveness on a real-world dataset.

• Analyze the concept of kernel ridge regression. How does kernel ridge regression extend linear regression to non-linear problems using kernels, and what are the benefits of this approach? Implement kernel ridge regression in Rust and apply it to a complex regression task.

• Explore the use of Multiple Kernel Learning (MKL). How does MKL combine multiple kernels to improve model performance, and what are the challenges of learning the optimal combination of kernels? Implement MKL in Rust and compare its performance with single kernel methods on a benchmark dataset.

• Discuss the application of kernel methods in bioinformatics. How can kernel methods be used to analyze biological data, such as gene expression or protein-protein interactions, and what are the advantages of using kernels in this domain? Implement a kernel-based bioinformatics application in Rust and evaluate its performance.

• Analyze the use of kernels in image processing tasks. How do kernel methods enable the modeling of complex image features, and what are the challenges of applying kernels to high-dimensional image data? Implement a kernel-based image classification system in Rust and evaluate its accuracy.

• Explore the concept of kernelized clustering. How do kernel methods extend traditional clustering algorithms like k-means to capture non-linear clusters, and what are the benefits of this approach? Implement kernel k-means in Rust and apply it to a dataset with non-linear clusters.

• Discuss the role of kernels in natural language processing (NLP). How can kernel methods be used to model text data, such as in tasks like text classification or sentiment analysis, and what are the challenges of applying kernels to NLP? Implement a kernel-based NLP application in Rust and evaluate its performance.

• Analyze the trade-offs between different kernel functions. How do linear, polynomial, and Gaussian kernels differ in terms of complexity, interpretability, and computational efficiency, and when should each be used? Implement and compare different kernels in Rust on a multi-class classification task.

• Explore the concept of the reproducing kernel Hilbert space (RKHS). How does RKHS provide a mathematical framework for understanding kernel methods, and what are its implications for kernel-based learning algorithms? Implement an RKHS-based kernel method in Rust and apply it to a real-world problem.

• Discuss the advantages of using kernel methods in high-dimensional spaces. How do kernel methods mitigate the curse of dimensionality, and what are the best practices for applying them to high-dimensional data? Implement a kernel method in Rust for a high-dimensional dataset and evaluate its performance.

• Analyze the impact of regularization in kernel methods. How does regularization prevent overfitting in kernel-based models, and what techniques can be used to balance bias and variance? Implement a regularized kernel method in Rust and experiment with different regularization parameters.

• Explore the future directions of research in kernel methods. What are the emerging trends and challenges in the field of kernel methods, and how can advances in machine learning and AI contribute to the development of more powerful and efficient kernel algorithms? Implement a cutting-edge kernel method in Rust and experiment with its application to a real-world problem.

Each prompt encourages you to think critically and apply what you learn to solve complex, non-linear problems in machine learning. Embrace these challenges as opportunities to deepen your expertise and push the boundaries of your knowledge, using Rust to unlock the full potential of Kernel Methods.

15.8.2. Hands On Practices link

These exercises are designed to be challenging and in-depth, requiring you to apply both theoretical knowledge and practical skills in Rust.