17.1. Introduction to AutoML link

AutoML, or Automated Machine Learning, represents a significant shift in the way machine learning models are developed and deployed by reducing the complexity of traditional workflows. At its core, AutoML automates critical stages of the machine learning pipeline, such as model selection, hyperparameter tuning, and feature engineering, thereby lowering the barrier to entry for non-experts while increasing efficiency for experienced practitioners. The traditional machine learning process is often time-consuming, requiring significant expertise across various stages, including data preprocessing, feature selection, and algorithm optimization. AutoML addresses these challenges by providing systematic, automated approaches to streamline these tasks, allowing users to focus more on high-level problem solving rather than getting mired in the technical details of model building.

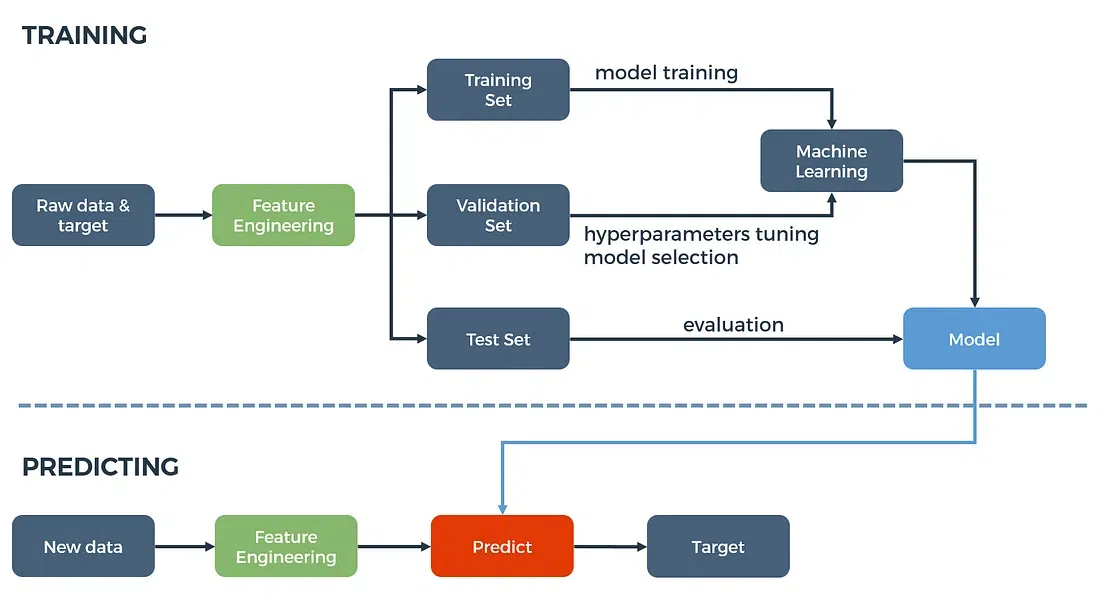
Figure 1: Traditional machine learning approach for training and predicting (or inference).

The motivation for AutoML is rooted in the complexity and resource demands of traditional machine learning workflows. In a typical machine learning pipeline, the process begins with data collection and preprocessing, followed by the selection of a suitable model architecture, tuning hyperparameters, and finally, evaluating the model on test data. Each of these steps demands a deep understanding of the underlying algorithms and the problem domain. For example, model selection involves choosing from a wide array of potential algorithms, such as decision trees, support vector machines, or neural networks, each of which has its own set of strengths and weaknesses. Similarly, hyperparameter tuning is a non-trivial task that involves optimizing parameters like learning rates, regularization terms, and model complexity to prevent overfitting while maximizing performance.

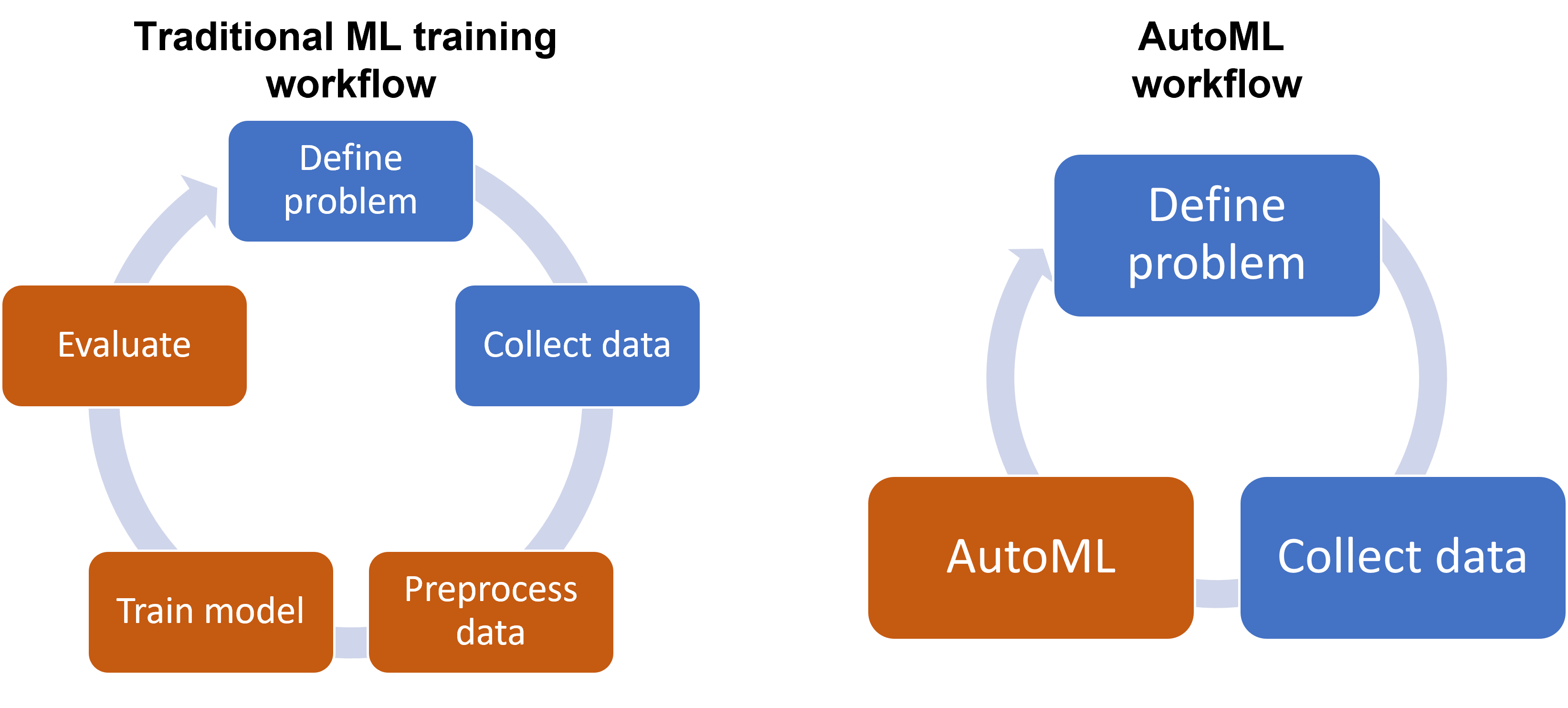
Figure 2: Key concept in AutoML approach.

Formally, let $\mathcal{D} = \{(x_i, y_i)\}_{i=1}^{N}$ represent a dataset consisting of $N$ input-output pairs, where $x_i \in \mathbb{R}^d$ is a feature vector and $y_i \in \mathbb{R}$ is the corresponding target value. The goal of machine learning is to find a model $f(x, \theta)$, parameterized by $\theta$, that minimizes a loss function $\mathcal{L}(y, f(x, \theta))$, which measures the difference between the predicted and actual target values. In traditional workflows, selecting the optimal model $f(x, \theta)$ involves manually comparing different architectures and hyperparameters, often through trial and error. Hyperparameter tuning is typically framed as an optimization problem:

$$ \theta^* = \arg \min_{\theta} \mathcal{L}(y, f(x, \theta)), $$

where $\theta^*$ represents the optimal set of hyperparameters that minimizes the loss function over the training data. Grid search or random search methods are commonly used for this task, but these methods can be computationally expensive, particularly when the hyperparameter space is large.

AutoML automates this process by employing intelligent search algorithms, such as Bayesian optimization, that efficiently explore the hyperparameter space. Bayesian optimization models the hyperparameter tuning process as a probabilistic function, seeking to minimize the expected loss by selecting hyperparameter configurations based on prior knowledge and iterative updates. This approach allows AutoML systems to converge more quickly to optimal solutions compared to exhaustive grid search, especially in high-dimensional hyperparameter spaces. Mathematically, Bayesian optimization defines a surrogate model, $g(\theta)$, which approximates the true objective function $\mathcal{L}(y, f(x, \theta))$, and selects the next hyperparameter configuration $\theta$ based on an acquisition function that balances exploration and exploitation:

$$ \theta_{\text{next}} = \arg \max_{\theta} \mathcal{A}(\theta | g(\theta), \mathcal{D}). $$

Here, $\mathcal{A}$ represents the acquisition function, which suggests the next set of hyperparameters to evaluate based on the current knowledge of the loss surface. This process iteratively refines the surrogate model until the optimal hyperparameters are found.

In addition to hyperparameter tuning, AutoML also automates model selection. AutoML frameworks evaluate multiple model architectures, such as linear models, decision trees, or ensemble methods like Gradient Boosting, and select the one that best fits the data. The model selection process can be formalized as a combinatorial optimization problem, where the goal is to choose the model $f$ and hyperparameters $\theta$ that jointly minimize the loss function over the dataset:

$$ (f^*, \theta^*) = \arg \min_{f, \theta} \mathcal{L}(y, f(x, \theta)). $$

AutoML frameworks typically implement strategies like cross-validation to estimate the generalization performance of different models and hyperparameter combinations, ensuring that the selected model performs well on unseen data.

Feature engineering, another critical aspect of the machine learning pipeline, is also automated in AutoML systems. Feature engineering involves transforming raw data into meaningful input features that can improve the performance of the learning algorithm. Traditional feature engineering requires domain expertise and manual experimentation to identify relevant features, create interaction terms, and handle missing values. AutoML automates this process by using techniques such as feature selection algorithms, which rank features based on their importance to the predictive model, and feature transformation methods, such as polynomial expansion or binning. These automated feature engineering techniques ensure that the model can capture the complex relationships within the data, without requiring extensive manual intervention.

An AutoML pipeline typically consists of multiple stages: data preprocessing, model selection, hyperparameter tuning, and model evaluation. During the data preprocessing stage, AutoML systems clean the data by handling missing values, normalizing numerical features, and encoding categorical variables. Model selection follows, where the system evaluates a variety of models to determine which one is best suited to the data. Next, hyperparameter optimization is performed, refining the model by adjusting key parameters to minimize the loss function. Finally, the selected model is evaluated on a holdout set or through cross-validation to ensure that it generalizes well to unseen data.

The automation provided by AutoML is not without trade-offs. While it simplifies the process and makes machine learning more accessible, it can also reduce the level of control and interpretability that practitioners have over their models. For example, in highly regulated industries like healthcare or finance, the transparency of model decisions is crucial for compliance and trust. Although AutoML frameworks are increasingly incorporating techniques for model explainability, such as SHAP values or LIME (Local Interpretable Model-agnostic Explanations), practitioners must still balance the benefits of automation with the need for interpretability and domain-specific customization.

In practical terms, implementing AutoML in Rust involves leveraging libraries that can handle tasks such as model selection, hyperparameter optimization, and feature engineering. Rust’s performance and safety features make it an ideal language for building efficient AutoML systems that scale to large datasets and computationally intensive tasks. By combining Rust’s low-level control with automated machine learning techniques, developers can create robust, high-performance models with minimal manual intervention.

In conclusion, AutoML is revolutionizing the machine learning landscape by automating critical stages of the modeling process, such as model selection, hyperparameter tuning, and feature engineering. These automated systems reduce the complexity of traditional workflows, making machine learning more accessible to non-experts and significantly improving efficiency for experienced practitioners. By streamlining the process of building, optimizing, and deploying models, AutoML enables faster and more effective machine learning solutions, while still posing important considerations regarding transparency and interpretability in certain applications.

To illustrate the concepts of AutoML practically, we can implement a basic AutoML pipeline in Rust, focusing on automating the model selection process. For this demonstration, we will use a simple dataset, such as the Iris dataset, which is commonly used in machine learning for classification tasks.

First, we need to prepare our Rust environment. We will utilize the ndarray crate for handling numerical operations and the linfa crate for implementing machine learning algorithms.

// Cargo.toml
[dependencies]
ndarray = "0.15"
linfa = "0.7"
linfa-trees = "0.7"
linfa-logistic = "0.7"

Next, let’s load the Iris dataset and split it into training and testing sets. The following code snippet demonstrates how to do this:

use ndarray;
use linfa;
use linfa_trees;
use linfa_logistic;

use ndarray::{Array2, Array1};
use linfa::prelude::*;
use linfa::Dataset;
use linfa_trees::DecisionTree;
use linfa_logistic::LogisticRegression;

fn load_iris_dataset_binary() -> (Array2<f64>, Array1<usize>) {
    // Example: Randomly generated dummy data with correct shapes
    // 100 samples, 4 features per sample for binary classification
    let features = Array2::from_shape_vec((100, 4), (0..400).map(|x| x as f64).collect()).unwrap();
    
    // 100 labels corresponding to the samples (2 classes: 0 and 1)
    let labels = Array1::from_vec((0..100).map(|x| x % 2).collect());
    
    (features, labels)
}

fn main() {
    let (features, labels) = load_iris_dataset_binary();
    let dataset = Dataset::new(features, labels).split_with_ratio(0.8);
    let (train, test) = dataset;

    // Decision Tree Classifier
    let decision_tree = DecisionTree::params().fit(&train).unwrap();
    let tree_predictions = decision_tree.predict(&test);
    let tree_accuracy = tree_predictions.confusion_matrix(&test).unwrap().accuracy();
    println!("Decision Tree accuracy: {}", tree_accuracy);

    // Logistic Regression
    let logistic_regression = LogisticRegression::new().fit(&train).unwrap();
    let log_reg_predictions = logistic_regression.predict(&test);
    let log_reg_accuracy = log_reg_predictions.confusion_matrix(&test).unwrap().accuracy();
    println!("Logistic Regression accuracy: {}", log_reg_accuracy);
}

In this example, we first load the Iris dataset and split it into training and testing sets. We then initialize a collection of models, which in this case include a decision tree classifier and a logistic regression model. For each model, we fit it to the training data and evaluate its performance on the test set by calculating accuracy. This simple implementation serves as a foundational step in building an AutoML pipeline that automates the model selection process.

In conclusion, AutoML represents a significant advancement in the field of machine learning, providing practical solutions to the challenges faced by data scientists. By understanding the fundamental ideas, conceptual frameworks, and practical implementations of AutoML, practitioners can better leverage its capabilities and navigate the complexities of the machine learning landscape. Rust, with its performance and safety features, offers a robust environment for implementing AutoML solutions, making it an excellent choice for developers looking to explore this exciting area of machine learning.

17.2. Automated Feature Engineering link

Automated feature engineering is a critical aspect of the machine learning pipeline, as the quality of features derived from raw data significantly impacts the performance and accuracy of predictive models. Feature engineering involves the process of extracting, transforming, and selecting relevant features from raw data to ensure that the machine learning algorithms can effectively capture the underlying patterns. By automating this process, practitioners can reduce manual effort and improve consistency, particularly in large-scale and complex datasets, where manual feature generation would be inefficient and prone to error.

To understand the theoretical framework behind automated feature engineering, it is important to start with the definition of features. In machine learning, a feature is a measurable property or characteristic of the phenomenon being modeled. Mathematically, given a dataset $\mathcal{D} = \{(x_i, y_i)\}_{i=1}^N$, where $x_i \in \mathbb{R}^d$ represents a feature vector and $y_i \in \mathbb{R}$ represents the corresponding target variable, feature engineering focuses on transforming the raw data $x_i$ into more informative representations that improve the model’s ability to predict $y_i$. The process is typically divided into three primary stages: feature extraction, feature transformation, and feature selection.

Feature extraction is the process of identifying relevant information from raw data that can be converted into features. Formally, this involves mapping raw data $X$ to a new feature space $\Phi(X)$, where $\Phi$ is a feature extraction function designed to capture useful properties of the data. For example, in the case of textual data, $\Phi$ might involve tokenizing the text into individual words or phrases, while for time-series data, $\Phi$ might involve extracting statistical features such as moving averages or variance over time. Feature extraction is particularly crucial in domains like natural language processing, image analysis, and signal processing, where raw data often contains unstructured or high-dimensional information that needs to be transformed into a structured format suitable for machine learning algorithms.

Feature transformation is the next critical step in the feature engineering process. In this phase, the extracted features are transformed into forms that better suit the learning algorithm. Mathematically, this can be viewed as applying a transformation function $T: \mathbb{R}^d \to \mathbb{R}^d$ to the feature vectors. For instance, in regression or classification tasks, numerical features may need to be scaled or normalized to ensure that they lie within a similar range, preventing any single feature from disproportionately influencing the model. Transformation can also involve encoding categorical features, using methods such as one-hot encoding or target encoding. Polynomial feature generation, where new features are created as polynomial combinations of existing features, is another transformation technique commonly used to capture non-linear relationships within the data. For example, if a dataset contains features $x_1$ and $x_2$, generating polynomial features might include constructing new features such as $x_1^2$, $x_2^2$, or $x_1 \cdot x_2$, which can help linear models capture non-linear patterns in the data.

Feature selection is the final stage, and it involves identifying which features are most relevant to the predictive task while discarding redundant or irrelevant features. Formally, given a feature set $\{x_1, x_2, \dots, x_d\}$, the goal of feature selection is to find a subset $\{x_{i_1}, x_{i_2}, \dots, x_{i_k}\}$, where $k < d$, that maximizes the predictive power of the model while reducing overfitting and improving interpretability. Feature selection methods can be classified into three main categories: filter methods, wrapper methods, and embedded methods. Filter methods rank features based on statistical metrics such as correlation coefficients, mutual information, or variance, independently of the learning algorithm. Wrapper methods, on the other hand, evaluate feature subsets based on their performance with a specific model, typically using a search strategy such as forward selection or backward elimination. Embedded methods, such as L1 regularization (Lasso), integrate feature selection directly into the model training process by penalizing less important features and driving their coefficients toward zero.

One of the key challenges in automated feature engineering is handling the vast diversity of data types and ensuring that the engineered features are tailored to the specific problem. The mathematical and statistical properties of the data must be considered when designing automated pipelines. For example, time-series data may require lag features or rolling-window statistics, whereas image data may benefit from automated feature extraction using convolutional neural networks (CNNs) that generate hierarchical features from pixel intensities. The complexity of selecting appropriate techniques for different types of data underscores the importance of designing automated feature engineering systems that can adapt to the specific characteristics of the dataset.

In the context of automated feature engineering, the role of dimensionality reduction techniques, such as Principal Component Analysis (PCA), becomes crucial, particularly when dealing with high-dimensional data. PCA aims to reduce the dimensionality of the dataset by finding a new set of orthogonal axes that maximize the variance in the data. Mathematically, PCA involves solving the eigenvalue problem for the covariance matrix of the data $\Sigma = \frac{1}{N} \sum_{i=1}^N (x_i - \bar{x})(x_i - \bar{x})^TΣ=N$, where $\bar{x}$ is the mean of the feature vectors. The resulting eigenvectors represent the principal components, and the corresponding eigenvalues represent the amount of variance captured by each component. By selecting only the top $k$ principal components, where $k$ is chosen based on the cumulative variance explained by the components, PCA reduces the number of features while preserving as much information as possible. This reduction in dimensionality helps mitigate the risk of overfitting, particularly in models where the number of features is large relative to the number of observations.

Automating the feature engineering process poses several technical challenges. First, the sheer variety of available feature extraction and transformation techniques means that choosing the right methods for a given dataset is non-trivial. Second, automated feature engineering must balance generalization and model complexity, as generating too many features can lead to overfitting, especially in high-dimensional spaces. Finally, computational efficiency is a key consideration, as automated feature engineering systems must be capable of scaling to large datasets while maintaining reasonable training times.

In summary, automated feature engineering is a powerful tool that transforms raw data into informative features that improve the performance of machine learning models. Through automated extraction, transformation, and selection of features, machine learning workflows become more efficient, reducing the need for manual intervention and domain expertise. While the process of automating feature engineering presents challenges, particularly in selecting the right techniques for different types of data, advancements in machine learning algorithms and frameworks have made it possible to implement robust and scalable automated feature engineering systems. By leveraging these techniques, practitioners can significantly enhance the predictive accuracy of their models, while also reducing the risk of overfitting and improving model interpretability.

In the realm of practical implementation, utilizing Rust for automated feature engineering can offer significant advantages, particularly in terms of performance and safety. Rust's strong type system and memory safety features make it an excellent choice for developing robust machine learning applications. To demonstrate how automated feature engineering can be implemented in Rust, let's consider a practical example involving a dataset that contains information about housing prices.

Step 1: Define the Dataset Structure link

In this step, we define a struct called House to represent the dataset. This struct contains attributes such as bedrooms, square_feet, neighborhood_quality, and price. Each of these attributes represents a feature of the house. For instance, bedrooms is an integer representing the number of bedrooms, square_feet is a floating-point number indicating the total area of the house, neighborhood_quality is a string describing the quality of the neighborhood, and price is the price of the house. The create_dataset function initializes a vector of House instances with sample data. This dataset forms the basis for all subsequent data processing and model training steps.

#[derive(Debug, Clone)]
struct House {
    bedrooms: u32,
    square_feet: f64,
    neighborhood_quality: String,
    price: f64,
}

fn create_dataset() -> Vec<House> {
    vec![
        House { bedrooms: 3, square_feet: 1500.0, neighborhood_quality: "Good".to_string(), price: 300000.0 },
        House { bedrooms: 4, square_feet: 2000.0, neighborhood_quality: "Excellent".to_string(), price: 500000.0 },
        House { bedrooms: 2, square_feet: 800.0, neighborhood_quality: "Fair".to_string(), price: 150000.0 },
        // Add more data samples...
    ]
}

Step 2: Implement Feature Transformation link

Feature transformation is a crucial preprocessing step that prepares the data for machine learning models. In this step, we normalize the square_feet feature by dividing it by the maximum value in the dataset, which scales the feature to a range between 0 and 1. This normalization ensures that all features contribute equally to the model training. Additionally, we encode the neighborhood_quality feature, which is categorical, into numerical values. For example, "Excellent" is mapped to 3, "Good" to 2, and "Fair" to 1. This conversion is necessary because machine learning algorithms typically require numerical input.

fn transform_features(houses: &mut Vec<House>) {
    let max_square_feet = houses.iter().map(|h| h.square_feet).fold(0.0, f64::max);
    
    for house in houses.iter_mut() {
        house.square_feet /= max_square_feet; // Normalize square footage
        
        // Encode neighborhood quality
        house.neighborhood_quality = match house.neighborhood_quality.as_str() {
            "Excellent" => 3,
            "Good" => 2,
            "Fair" => 1,
            _ => 0,
        }.to_string();
    }
}

Step 3: Implement Feature Selection link

Feature selection helps in identifying the most relevant features for the model. Here, a heuristic approach is used where features are selected based on their correlation with the target variable (price). We calculate the average price and filter out features whose values have a significant deviation from this average, as specified by a threshold. This step is crucial to reduce dimensionality and improve model performance by keeping only those features that have a strong relationship with the target variable.

fn select_features(houses: &Vec<House>, threshold: f64) -> Vec<House> {
    let avg_price: f64 = houses.iter().map(|h| h.price).sum::<f64>() / houses.len() as f64;

    houses.iter()
        .filter(|house| {
            // Simple heuristic based on price correlation
            (house.bedrooms as f64 - avg_price).abs() > threshold ||
            (house.square_feet - avg_price).abs() > threshold
        })
        .cloned()
        .collect()
}

Step 4: Train-Test Split link

To evaluate the performance of the model, the dataset is split into training and testing sets. This split is done using a specified ratio, with the majority of data used for training and the remainder reserved for testing. This ensures that the model is trained on one subset of data and evaluated on another, which helps in assessing its generalization capability. In this step, train_test_split calculates the number of samples for the training set and creates two separate vectors for training and testing data.

fn train_test_split(houses: &Vec<House>, train_ratio: f64) -> (Vec<House>, Vec<House>) {
    let train_size = (houses.len() as f64 * train_ratio) as usize;
    let train_data = houses[..train_size].to_vec();
    let test_data = houses[train_size..].to_vec();
    (train_data, test_data)
}

Step 5: Train and Evaluate the Model link

In this step, a model is trained using the training data and its performance is evaluated on the testing data. The train_model function is a placeholder where actual model training logic would be implemented. After training, the model's accuracy is assessed using the evaluate method. We then apply feature engineering, including transformation and selection, and retrain the model to see if these steps improve performance. This comparison provides insight into the impact of feature engineering on the model's accuracy.

fn train_model(_train_data: Vec<House>) -> Model {
    // Placeholder for model training logic
    Model {}
}

struct Model {}

impl Model {
    fn evaluate(&self, _test_data: Vec<House>) -> f64 {
        // Placeholder for model evaluation logic
        0.75 // Dummy accuracy
    }
}

fn evaluate_model(houses: Vec<House>) {
    let (train_data, test_data) = train_test_split(&houses, 0.8);
    
    let model = train_model(train_data);
    let accuracy_before = model.evaluate(test_data);

    println!("Model accuracy before feature engineering: {}", accuracy_before);
    
    // Apply feature engineering
    let mut houses_engineered = houses.clone();
    transform_features(&mut houses_engineered);
    let selected_houses = select_features(&houses_engineered, 0.1);
    
    let (train_data_engineered, test_data_engineered) = train_test_split(&selected_houses, 0.8);

    let model_engineered = train_model(train_data_engineered);
    let accuracy_after = model_engineered.evaluate(test_data_engineered);

    println!("Model accuracy after feature engineering: {}", accuracy_after);
}

Step 6: Main Function link

The main function serves as the entry point of the program, where it integrates all previous steps. It initializes the dataset using create_dataset and then calls evaluate_model to perform the entire process of training, feature engineering, and evaluation. This function demonstrates how the different components work together and provides a way to run the entire workflow in a single execution.

fn main() {
    let dataset = create_dataset();
    evaluate_model(dataset);
}

In conclusion, the process of feature engineering is pivotal in constructing robust machine learning models, and the example provided illustrates a comprehensive approach to transforming and selecting features to enhance model performance. By normalizing numerical data and encoding categorical variables, we prepare the dataset for effective model training. The feature selection step helps in identifying the most significant features, improving both the efficiency and accuracy of the model. Leveraging Rust's performance and safety features, we implement a reliable framework for data preprocessing and model evaluation. This practical implementation not only establishes a solid foundation for feature engineering but also paves the way for exploring advanced techniques, ultimately contributing to more efficient and effective machine learning workflows.

17.3. Model Selection and Hyperparameter Tuning link

Automated model selection and hyperparameter tuning are essential techniques in machine learning, enabling practitioners to optimize their models by systematically exploring various configurations and hyperparameters. These techniques significantly improve the performance of machine learning models by ensuring that the chosen model configuration is not only accurate but also generalizes well to unseen data. In this section, we delve into the theoretical underpinnings of these methods and present practical implementations using Rust, focusing on the ndarray, rand, and linfa crates. We will particularly emphasize grid search as a hyperparameter tuning technique, providing both the mathematical foundations and Rust-based examples.

Automated model selection refers to the process of evaluating multiple candidate models to determine which performs best under specific criteria. Mathematically, let $\mathcal{M} = \{ M_1, M_2, \dots, M_k \}$ be the set of candidate models, where each $M_i$ represents a different model architecture or configuration. The goal of model selection is to find the model $M^* \in \mathcal{M}$ that minimizes a predefined loss function $\mathcal{L}(M, \mathcal{D})$ over the validation data $\mathcal{D}$. The loss function could represent various metrics, such as Mean Squared Error (MSE) for regression tasks or accuracy for classification tasks. Formally, model selection can be described as solving the following optimization problem:

$$ M^* = \arg \min_{M \in \mathcal{M}} \mathcal{L}(M, \mathcal{D}_{\text{val}}), $$

where $\mathcal{D}_{\text{val}}$ is the validation set and $\mathcal{L}(M, \mathcal{D}_{\text{val}})$ is the model's performance metric on the validation data.

Hyperparameter tuning, on the other hand, refers to optimizing the external parameters of the model that govern its learning process. Hyperparameters, unlike model parameters learned during training, are set before the learning process begins and have a significant impact on the model's behavior. Common hyperparameters include the learning rate, tree depth (in decision trees), the number of hidden layers (in neural networks), and regularization strength. Mathematically, let $\Theta = \{ \theta_1, \theta_2, \dots, \theta_n \}$ represent the hyperparameter space, where $\theta_i$ denotes a specific hyperparameter. The goal of hyperparameter tuning is to find the optimal set of hyperparameters $\Theta^*$ that minimizes the validation loss:

$$ \Theta^* = \arg \min_{\Theta \in \mathcal{H}} \mathcal{L}(M(\Theta), $$

where $\mathcal{H}$ denotes the hyperparameter space and $M(\Theta)$ represents the model trained with the hyperparameters $\Theta$. Grid search is one of the most straightforward methods for hyperparameter tuning, where the algorithm exhaustively evaluates the model’s performance across a predefined grid of hyperparameter combinations.

In grid search, the hyperparameter space $\mathcal{H}$ is discretized into a finite set of values for each hyperparameter. Let $\theta_1 \in \{\theta_{1,1}, \theta_{1,2}, \dots, \theta_{1,m_1} \}$ represent the possible values for hyperparameter $\theta_1$, $\theta_2 \in \{\theta_{2,1}, \theta_{2,2}, \dots, \theta_{2,m_2} \}$ for hyperparameter $\theta_2$, and so on. The total number of combinations to evaluate is the Cartesian product of the hyperparameter sets:

$$ \mathcal{H}| = m_1 \times m_2 \times \dots \times m_n. $$

Each combination of hyperparameters is evaluated by training the model on the training data $\mathcal{D}_{\text{train}}$ and computing the validation loss on $\mathcal{D}_{\text{val}}$. The optimal set of hyperparameters $\Theta^*$ is the one that minimizes the validation loss over all evaluated combinations. While grid search is simple to implement, it can be computationally expensive, especially when the number of hyperparameters is large. Nonetheless, it remains a popular choice for small to moderate-sized hyperparameter spaces, particularly when paired with efficient validation techniques like cross-validation.

To implement automated model selection and hyperparameter tuning in Rust, we can leverage the ndarray, rand, and linfa crates. The ndarray crate provides a powerful library for working with N-dimensional arrays, which are essential for managing datasets and model parameters. The rand crate is useful for generating random numbers and sampling hyperparameter combinations in more advanced search methods like random search. The linfa crate, which is a machine learning toolkit for Rust, offers utilities for training and evaluating models, allowing seamless integration of model selection and hyperparameter tuning.

A basic implementation of grid search for hyperparameter tuning in Rust might involve the following steps:

• Define the hyperparameter grid by specifying the range of values for each hyperparameter.

• Iterate over all possible hyperparameter combinations.

• For each combination, train the model on the training data and compute the performance metric on the validation data.

• Track the combination that yields the best validation performance.

• Return the optimal set of hyperparameters.

In Rust, we use the ndarray crate for numerical operations and the linfa crate for machine learning algorithms. The rand and rand_distr crates help generate random data for testing purposes. We will demonstrate both grid search and random search techniques for hyperparameter tuning, starting with a practical implementation of grid search.

The provided code demonstrates a grid search approach to tune the hyperparameters of a linear regression model. It includes generating random data, defining hyperparameter grids, training models, and evaluating their performance.

The Cargo.toml file specifies the dependencies required for the project. We include the ndarray crate for numerical operations, rand and rand_distr for generating random data, and linfa and linfa-linear for machine learning functionalities.

[dependencies]
ndarray = "0.15"
ndarray-rand = "0.15"
rand = "0.8"
rand_distr = "0.4"
linfa = "0.7"  
linfa-linear = "0.7"

In the main.rs file, we first import the necessary modules. We create synthetic datasets using random values from a standard normal distribution to simulate feature and target data.

use ndarray::{Array1, Array2};
use rand::Rng;
use rand_distr::StandardNormal;
use linfa::prelude::*;
use linfa_linear::LinearRegression;
use std::time::Instant;

fn main() {
    let mut rng = rand::thread_rng();

    // Create a 2D array (100 samples, 2 features) with random values from a standard normal distribution
    let features: Array2<f64> = Array2::from_shape_fn((100, 2), |_| rng.sample(StandardNormal));

    // Create a 1D array (100 samples) with random values from a standard normal distribution
    let targets: Array1<f64> = Array1::from_shape_fn(100, |_| rng.sample(StandardNormal));

    // Define hyperparameter grid
    let learning_rates = vec![0.001, 0.01, 0.1];
    let regularization_strengths = vec![0.1, 1.0, 10.0];

    let mut best_score = f64::INFINITY;
    let mut best_params = (0.0, 0.0);

    let start_time = Instant::now();

    for &lr in &learning_rates {
        for &reg in &regularization_strengths {
            // Convert to Dataset
            let dataset = Dataset::new(features.clone(), targets.clone());

            // Create LinearRegression object
            let lin_reg = LinearRegression::default();

            // Train the model with the current hyperparameters
            let model = lin_reg.fit(&dataset).unwrap();

            // Evaluate the model
            let predictions = model.predict(dataset.records());

            // If predictions are 2D with one column, convert to Array1<f64>
            let predictions: Array1<f64> = if predictions.ndim() == 2 && predictions.shape()[1] == 1 {
                predictions.iter().cloned().collect()
            } else if predictions.ndim() == 1 {
                predictions
            } else {
                panic!("Predictions have an unexpected shape: {:?}", predictions.shape());
            };

            // Calculate Mean Squared Error
            let score = mean_squared_error(&targets, &predictions);

            // Update best score and parameters
            if score < best_score {
                best_score = score;
                best_params = (lr, reg);
            }
        }
    }

    let duration = start_time.elapsed();
    println!("Best hyperparameters: {:?}", best_params);
    println!("Best score (MSE): {}", best_score);
    println!("Execution time: {:?}", duration);
}

// Calculate Mean Squared Error manually
fn mean_squared_error(y_true: &Array1<f64>, y_pred: &Array1<f64>) -> f64 {
    if y_true.len() != y_pred.len() {
        panic!("y_true and y_pred sizes do not match!");
    }
    let squared_errors = (y_true - y_pred).mapv(|x| x.powi(2));
    squared_errors.mean().unwrap_or(f64::INFINITY)
}

In this code, we use grid search to find the best combination of learning rates and regularization strengths. The synthetic dataset is used for training and evaluation. After training models with different hyperparameter combinations, the code evaluates them using mean squared error (MSE) and identifies the best-performing set of parameters.

The build.rs file is used for specifying additional build instructions, such as linking to native libraries. Here, it ensures that the necessary LAPACK and BLAS libraries are linked, which are often required for linear algebra operations.

fn main() {
    println!("cargo:rustc-link-search=native=C:/Users/User/vcpkg/installed/x64-windows/lib");
    println!("cargo:rustc-link-lib=dylib=lapack");
    println!("cargo:rustc-link-lib=dylib=blas");
}

This configuration is crucial for ensuring that the linear algebra operations required by linfa-linear can be properly executed, allowing the model training and evaluation to run smoothly.

By incorporating these methods and configurations into your Rust-based machine learning workflow, you can effectively automate the process of model selection and hyperparameter tuning, leading to more accurate and robust models.

17.4. Neural Architecture Search (NAS) link

Neural Architecture Search (NAS) represents a transformative approach within the broader field of AutoML, specifically focusing on automating the design and optimization of neural network architectures. Traditionally, designing neural networks has been a labor-intensive task that heavily relies on expert knowledge and manual experimentation. The sheer number of hyperparameters and architectural choices—ranging from the number of layers, types of layers (e.g., convolutional, recurrent), activation functions, and connectivity patterns—creates a vast and complex search space. Navigating this search space efficiently to identify high-performing architectures is a central challenge that NAS addresses.

Formally, NAS can be defined as an optimization problem over a discrete search space $\mathcal{A}$ that contains all possible neural network architectures. Given a task $T$ and a dataset $\mathcal{D}$, the goal is to find an architecture $A^* \in \mathcal{A}$ that minimizes a performance metric $\mathcal{L}(A, \mathcal{D}, T)$, typically the validation loss, where $A$ denotes a candidate architecture. Mathematically, NAS can be written as:

$$ A^* = \arg \min_{A \in \mathcal{A}} \mathcal{L}(A, \mathcal{D}_{\text{val}}, T), $$

where $\mathcal{D}_{\text{val}}$ is the validation set, and $\mathcal{L}(A, \mathcal{D}_{\text{val}}, T)$ represents the performance of the architecture $A$ on the validation data for task $T$. The challenge lies in the fact that $\mathcal{A}$ is typically very large, potentially infinite, making brute-force search impractical.

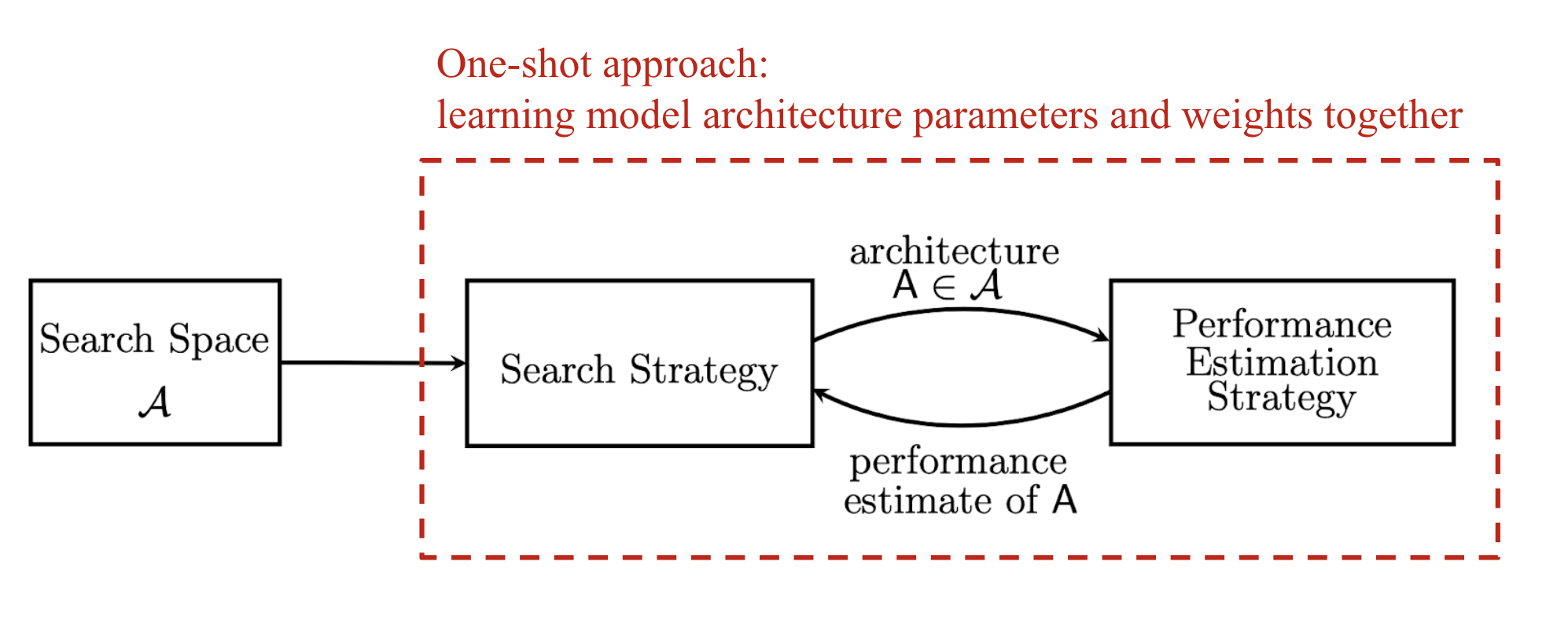
Figure 3: Key concept of NAS model.

The NAS search space defines a range of possible operations (e.g., convolution, fully-connected layers, pooling) and their allowable connections to construct valid neural network architectures. Human expertise plays a significant role in designing the search space, which can introduce biases. The search algorithm explores this space by sampling various architecture candidates, using performance metrics like accuracy or latency as rewards to optimize and find high-performing models. Finally, an evaluation strategy is employed to measure or estimate the performance of these candidates, often requiring significant computational resources, although newer methods aim to reduce this cost.

To efficiently explore this large space, NAS employs various optimization and search strategies such as reinforcement learning, evolutionary algorithms, and gradient-based methods. Each of these approaches introduces a distinct mechanism for proposing and evaluating architectures, balancing the trade-off between exploration (searching for new, potentially better architectures) and exploitation (refining architectures known to perform well).

Reinforcement learning (RL) has emerged as a prominent method for NAS, leveraging its strength in solving sequential decision-making problems. In the context of NAS, the problem is framed as a Markov Decision Process (MDP), where the agent sequentially constructs a neural architecture by selecting layers, activation functions, and other design elements. The state of the MDP corresponds to the partially constructed architecture, and the action space consists of the possible design choices (e.g., adding a convolutional layer or a fully connected layer). The reward signal is derived from the performance of the fully constructed architecture, usually based on validation accuracy or loss. Over time, the agent learns to maximize this reward by generating architectures that lead to better model performance. Formally, the agent's objective is to maximize the expected reward $R(A)$, which is proportional to the performance of the architecture $A$ on the validation data:

$$ \max_{\pi} \mathbb{E}[R(A) | \pi], $$

where $\pi$ represents the policy that governs the agent's actions (i.e., architectural decisions), and $R(A)$ is the reward for the architecture $A$. The reinforcement learning approach excels in situations where sequential decision-making is critical, but it can be computationally expensive, as each action in the search involves training and evaluating a neural network.

Another class of approaches commonly used in NAS is evolutionary algorithms (EAs). Inspired by the principles of natural selection, EAs maintain a population of candidate architectures that evolve over successive generations. At each generation, new architectures are generated through genetic operations such as mutation and crossover. Mutation might involve altering a specific component of the architecture (e.g., changing a convolutional layer's kernel size), while crossover involves combining elements of two parent architectures to produce a new offspring. The fitness of each architecture in the population is evaluated based on its performance, and the best-performing architectures are selected to form the next generation. Mathematically, evolutionary algorithms optimize the population $P_t$ of architectures at generation $t$ by selecting architectures with high fitness values $F(A)$, where $F(A)$ is often the negative validation loss:

$$ P_{t+1} = \text{select}\left(\text{mutate}(\text{crossover}(P_t)), F(A)\right). $$

Evolutionary algorithms offer a broader exploration of the search space compared to reinforcement learning, as they maintain a diverse population of architectures. This diversity increases the likelihood of discovering novel, high-performing designs. However, like RL-based approaches, evolutionary algorithms can be computationally expensive due to the need to evaluate multiple candidate architectures across generations.

Gradient-based methods represent a more recent advancement in NAS, focusing on differentiable architecture search. These methods aim to relax the discrete search space into a continuous one, enabling gradient-based optimization techniques to be applied. In gradient-based NAS, the architecture parameters $\alpha$ are treated as continuous variables, allowing the use of backpropagation to compute gradients with respect to the architecture itself. The search process jointly optimizes the network weights $\theta$ and the architecture parameters $\alpha$. The objective is to minimize the validation loss $\mathcal{L}(\theta, \alpha, \mathcal{D})$ with respect to both $\theta$ and $\alpha$:

$$ \min_{\alpha} \min_{\theta} \mathcal{L}(\theta, \alpha, \mathcal{D}). $$

Gradient-based NAS methods are particularly efficient in terms of search time, as they eliminate the need to train and evaluate individual architectures separately. Instead, architectures are optimized directly through gradient descent, significantly reducing computational overhead. However, gradient-based NAS methods are more constrained in the types of architectures they can explore, as the search space must be differentiable.

Each NAS approach—whether reinforcement learning, evolutionary algorithms, or gradient-based methods—has its advantages and limitations. Reinforcement learning offers flexibility and adaptability, evolutionary algorithms provide diversity and broad exploration, and gradient-based methods offer computational efficiency. The choice of method depends on the specific problem at hand, the size of the search space, and the available computational resources.

In practical implementations using Rust, NAS can be integrated with machine learning frameworks such as linfa for training and evaluating architectures. Rust's performance capabilities make it well-suited for NAS, particularly for large-scale architecture searches where computational efficiency is critical. By leveraging parallelism and Rust’s memory safety features, NAS implementations in Rust can explore the architectural search space effectively while maintaining high performance and scalability.

In conclusion, Neural Architecture Search represents a powerful and flexible approach to automating the design of neural networks. By framing the search for optimal architectures as an optimization problem, NAS reduces the reliance on manual tuning and expert knowledge, allowing machine learning practitioners to discover high-performing architectures more efficiently. Whether using reinforcement learning, evolutionary algorithms, or gradient-based methods, NAS offers a systematic approach to navigating the complex search space of neural network design, ensuring that the resulting architectures are both high-performing and well-suited to the task at hand.

Implementing a simple NAS algorithm in Rust requires a solid understanding of both Rust's programming paradigms and the underlying principles of NAS. In this example, we will develop a basic evolutionary algorithm for neural architecture search. Our goal is to create a population of neural networks, evaluate their performance on a given dataset, and iteratively evolve the population to improve performance.

First, we need to set up our Rust project and include necessary dependencies. We will use the ndarray crate for handling numerical arrays and tch-rs for interfacing with PyTorch, which will allow us to define and train neural networks. Here’s a basic configuration for our Cargo.toml:

[dependencies]
ndarray = "0.15"
tch = "0.4"

Next, we can outline our evolutionary algorithm. The following example demonstrates how to define a simple neural network architecture and implement the evolutionary process:

use ndarray::Array2;
use tch::{nn, Device};

#[derive(Debug, Clone)]
struct Architecture {
    layers: Vec<usize>, // Vector to hold the number of neurons in each layer
}

impl Architecture {
    fn new(layers: Vec<usize>) -> Self {
        Self { layers }
    }

    // Function to create a neural network from the architecture
    fn create_model(&self, vs: &nn::Path) -> nn::Sequential {
        let mut model = nn::seq();
        for &layer_size in &self.layers {
            model = model.add(nn::linear(vs / "layer", layer_size as i64, layer_size as i64, Default::default()));
        }
        model
    }
}

// Function to evaluate the architecture
fn evaluate_architecture(architecture: &Architecture, _data: &Array2<f32>, _targets: &Array2<f32>) -> f32 {
    let vs = nn::VarStore::new(Device::cuda_if_available());
    let _model = architecture.create_model(&vs.root());

    // Here, we would implement training and evaluation logic for the model
    // For simplicity, we'll return a random performance score
    0.5 // Placeholder for performance score
}

// Function to mutate an architecture
fn mutate_architecture(architecture: &Architecture) -> Architecture {
    let mut new_layers = architecture.layers.clone();
    // Randomly modify the architecture (e.g., adding or removing layers)
    // For simplicity, we'll add a layer randomly
    new_layers.push(10); // Adding a layer with 10 neurons
    Architecture::new(new_layers)
}

// Main evolutionary algorithm function
fn evolutionary_search(data: Array2<f32>, targets: Array2<f32>, generations: usize, population_size: usize) {
    let mut population: Vec<Architecture> = vec![];

    // Initialize population with random architectures
    for _ in 0..population_size {
        let layers = vec![32, 64]; // Example architecture
        population.push(Architecture::new(layers));
    }

    for _ in 0..generations {
        // Evaluate population
        let mut scores: Vec<(Architecture, f32)> = population.iter()
            .map(|arch| (arch.clone(), evaluate_architecture(arch, &data, &targets)))
            .collect();

        // Sort architectures by score
        scores.sort_by(|a, b| b.1.partial_cmp(&a.1).unwrap());

        // Select the top architectures for reproduction
        let top_architectures: Vec<Architecture> = scores.iter()
            .take(population_size / 2)
            .map(|(arch, _)| arch.clone())
            .collect();

        // Create new population through mutation
        population = top_architectures.iter()
            .map(|arch| mutate_architecture(arch))
            .collect();
    }

    // Final evaluation on the best architecture
    let best_architecture = &population[0];
    println!("Best architecture: {:?}", best_architecture);
}

fn main() {
    // Sample data for demonstration
    let data = Array2::<f32>::zeros((100, 10)); // 100 samples, 10 features
    let targets = Array2::<f32>::zeros((100, 1)); // 100 target values

    evolutionary_search(data, targets, 10, 20);
}

In this example, we defined a simple Architecture struct to represent a neural network's architecture, which includes a vector of layer sizes. The create_model method constructs the neural network using the specified layer sizes. The evaluate_architecture function is a placeholder where we would implement training and evaluation logic, returning a performance score based on the model's effectiveness.

The mutate_architecture function demonstrates a simple mutation strategy where we add a new layer to the architecture. The main function, evolutionary_search, orchestrates the evolutionary process, initializing a population of architectures, evaluating their performance, selecting the top performers, and mutating them to form the next generation.

Through this implementation, we gain insights into how NAS can be effectively approached using evolutionary algorithms in Rust. Although this example is simplified, it captures the essence of NAS while allowing room for expansion and refinement. As we explore more sophisticated architectures and more complex evaluation strategies, the potential of NAS to automate the design of neural networks becomes increasingly evident.

17.5. Meta-Learning and Transfer Learning in AutoML link

In the domain of AutoML, meta-learning and transfer learning are powerful techniques that extend the capabilities of machine learning models to adapt and generalize across multiple tasks efficiently. These approaches are especially beneficial in scenarios where data is scarce, the acquisition of labeled data is expensive, or the model needs to be deployed quickly in new environments with minimal additional training. Meta-learning, often referred to as "learning to learn," focuses on designing models that improve their performance on new tasks by leveraging prior experience, while transfer learning enables models to transfer knowledge from one task to another related task, significantly reducing training time and improving accuracy in the new task.

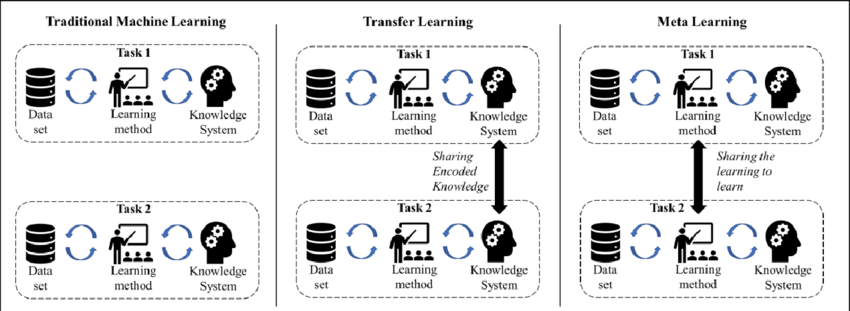
Figure 4: Traditional, transfer and meta learnings.

The core idea behind meta-learning is to enable models to adapt rapidly to new tasks by using knowledge acquired from prior learning experiences. This is formalized as a bi-level optimization problem, where at the outer level, the goal is to learn a meta-model $\theta_{\text{meta}}$ that can be fine-tuned to perform well on a variety of tasks, while at the inner level, task-specific parameters $\theta_T$ are optimized to minimize the loss for each individual task $T$. Let $\mathcal{T} = \{T_1, T_2, \dots, T_k\}$ represent a distribution of tasks, each characterized by its own dataset $\mathcal{D}_T$. The objective of meta-learning can be written as:

$$ \theta_{\text{meta}}^* = \arg \min_{\theta_{\text{meta}}} \sum_{T \in \mathcal{T}} \mathcal{L}_T(\theta_T^*), $$

where $\theta_T^* = \arg \min_{\theta_T} \mathcal{L}_T(\theta_T; \theta_{\text{meta}})$ represents the task-specific optimization. In other words, the meta-learning algorithm aims to find a set of meta-parameters $\theta_{\text{meta}}$ that can be quickly adapted to minimize the loss $\mathcal{L}_T$ on any given task $T$. This framework is commonly employed in few-shot learning, where the model is exposed to a limited number of examples from the target task and must learn to generalize effectively based on those few examples.

A common approach to meta-learning is Model-Agnostic Meta-Learning (MAML), which explicitly trains models to optimize quickly for new tasks with minimal data. Formally, MAML seeks to optimize the meta-parameters $\theta_{\text{meta}}$ such that the model can adapt to a new task after just a few gradient steps. The inner loop computes task-specific updates using gradient descent:

$$ \theta_T' = \theta_{\text{meta}} - \alpha \nabla_{\theta_{\text{meta}}} \mathcal{L}_T(\theta_{\text{meta}}), $$

where $\alpha$ is the learning rate for task adaptation. The outer loop then optimizes the meta-parameters based on the updated task-specific parameters $\theta_T'$ by minimizing the meta-objective across all tasks:

$$ \theta_{\text{meta}}^* = \arg \min_{\theta_{\text{meta}}} \sum_{T \in \mathcal{T}} \mathcal{L}_T(\theta_T'). $$

The strength of meta-learning lies in its ability to generalize across a variety of tasks, allowing the model to quickly learn new tasks with minimal data. This is particularly useful in AutoML systems, where the goal is to automate the selection of algorithms and hyperparameters that are most suitable for a given task based on previous performance across related tasks. Meta-learning, in this context, enables the AutoML system to "learn" from its own history of algorithm performance, thereby improving its decision-making over time.

Transfer learning complements meta-learning by providing a framework for transferring knowledge from a source task to a target task. In transfer learning, a model trained on a large dataset for a specific task is fine-tuned on a smaller dataset for a related task. The key assumption is that the knowledge acquired from the source task can be effectively reused to improve performance on the target task, particularly when the target dataset is limited in size. Formally, let $T_S$ represent the source task with a dataset $\mathcal{D}_S$, and $T_T$ represent the target task with a dataset $\mathcal{D}_T$, where $|\mathcal{D}_T| \ll |\mathcal{D}_S|$. The goal is to transfer the knowledge encoded in the parameters $\theta_S$ learned on the source task $T_S$ to initialize the parameters $\theta_T$ for the target task $T_T$. This can be expressed as:

$$ \theta_T^* = \arg \min_{\theta_T} \mathcal{L}_T(\theta_T; \theta_S), $$

where $\theta_T$ is initialized with $\theta_S$, and only a subset of parameters may be fine-tuned on the target task.

One of the most common applications of transfer learning is in deep learning models for computer vision. Pre-trained models, such as those trained on large datasets like ImageNet, capture generic features such as edges and textures in their initial layers. These pre-trained models can then be fine-tuned on smaller datasets for specific tasks, such as classifying medical images or detecting objects in satellite images, by updating only the task-specific layers while retaining the pre-trained weights for the lower layers. This approach drastically reduces the amount of data and computational resources required to train the model from scratch.

Transfer learning also finds application in natural language processing (NLP), where large language models pre-trained on extensive corpora can be fine-tuned for specific tasks such as sentiment analysis, machine translation, or question answering. By leveraging the linguistic knowledge captured during pre-training, transfer learning allows these models to generalize well on the target tasks, even when labeled data is scarce.

Both meta-learning and transfer learning significantly enhance the ability of machine learning models to generalize across tasks and datasets. Meta-learning focuses on improving a model’s adaptability by learning how to optimize efficiently for new tasks, while transfer learning enables models to reuse knowledge from previously learned tasks, thus reducing the computational and data requirements for new tasks. In the context of AutoML, these techniques play a crucial role in optimizing the selection of algorithms, hyperparameters, and neural architectures based on the specific characteristics of the task at hand.

In terms of implementation, both meta-learning and transfer learning can be integrated into Rust-based machine learning pipelines using libraries such as linfa for model training and evaluation. Rust’s performance and memory safety features make it an ideal candidate for developing scalable, high-performance AutoML systems that can handle large datasets and complex models. Additionally, Rust’s concurrency capabilities can be leveraged to parallelize the search over different hyperparameter configurations or neural architectures, further improving the efficiency of the AutoML process.

In conclusion, meta-learning and transfer learning are critical concepts in modern machine learning that enhance the adaptability and generalization of models across different tasks. By leveraging these techniques, AutoML systems can automate the design, training, and optimization of machine learning models, leading to more efficient and effective solutions in a wide range of applications.

In practical terms, implementing these techniques in Rust requires a solid understanding of machine learning libraries and frameworks that are compatible with Rust. While Rust's ecosystem for machine learning is still growing, libraries like tch-rs, which provides Rust bindings for PyTorch, can be utilized to implement meta-learning and transfer learning strategies. Additionally, the ndarray crate can be used for efficient numerical computations.

To illustrate the practical application of meta-learning and transfer learning in Rust, let's consider a scenario where we apply transfer learning to a dataset with limited data. Imagine we have a pre-trained model on a large dataset, and we wish to fine-tune it on a smaller dataset related to a similar task. Here's a simplified example of how this might look in Rust:

use tch;
use tch::{nn, Device, Tensor};
use tch::nn::{OptimizerConfig, Adam};
use tch::nn::ModuleT; // Import the ModuleT trait for forward_t

fn main() {
    let device = Device::cuda_if_available();
    let vs = nn::VarStore::new(device);

    // Define the model
    let model = nn::seq_t()
        .add(nn::linear(vs.root().sub("layer1"), 784, 256, Default::default()))
        .add_fn(|xs| xs.relu()) // Using relu function
        .add(nn::linear(vs.root().sub("layer2"), 256, 10, Default::default()));

    // Load your new dataset here
    let (train_images, train_labels) = load_my_dataset();
    
    // Fine-tuning the model with limited data
    let mut optimizer = Adam::default().build(&vs, 1e-3).unwrap();
    for epoch in 1..=20 {
        let outputs = model.forward_t(&train_images, true); // Use forward_t
        let loss = outputs.cross_entropy_for_logits(&train_labels);
        optimizer.backward_step(&loss);
        println!("Epoch: {}, Loss: {}", epoch, f64::from(&loss));
    }

    // Save the fine-tuned model
    vs.save("fine_tuned_model.ot").unwrap();
}

// Dummy function for loading dataset
fn load_my_dataset() -> (Tensor, Tensor) {
    // Replace with actual data loading logic
    let train_images = Tensor::randn(&[64, 784], (tch::Kind::Float, Device::cuda_if_available()));
    let train_labels = Tensor::randint(10, &[64], (tch::Kind::Int64, Device::cuda_if_available()));
    (train_images, train_labels)
}

In this code, we first set up a neural network model and load a pre-trained model's weights. We then load a new dataset, which is smaller, and proceed to fine-tune the model using this dataset. The model is trained over a few epochs, and we observe the loss to ensure the fine-tuning is effective.

Through the lens of meta-learning, we can implement few-shot learning techniques by simulating the scenario of learning from only a few examples. This could involve designing a model that can quickly adapt to new classes based on a limited number of samples. The implementation would involve creating a learning framework that evaluates the model's performance on various tasks and adjusts its learning strategy accordingly.

Evaluating the effectiveness of these strategies compared to traditional learning approaches is crucial. This can be achieved by comparing performance metrics such as accuracy, precision, recall, and F1-score on a validation set. Additionally, analyzing the training time and resource usage can provide insights into the efficiency of the meta-learning and transfer learning approaches.

In summary, meta-learning and transfer learning are powerful techniques within AutoML that enable models to learn more efficiently and effectively from limited data and related tasks. By implementing these strategies in Rust, we can leverage its performance and safety features while building robust machine learning systems capable of adapting to new challenges with minimal data. As the Rust ecosystem continues to evolve, the potential for advanced AutoML applications will only expand, paving the way for innovative solutions in machine learning.

17.6. Explainability and Interpretability in AutoML link

In the domain of AutoML, explainability and interpretability are foundational to ensuring that automated models not only deliver high performance but also generate insights that are comprehensible and trustworthy to end users. These concepts are essential, particularly as machine learning models are increasingly being deployed in high-stakes applications, such as healthcare, finance, and autonomous systems, where decision-makers must understand the underlying rationale behind model outputs. As AutoML automates processes such as model selection, hyperparameter tuning, and feature engineering, the complexity of the resulting models can increase, potentially turning them into "black boxes" that are difficult to interpret. This opacity in decision-making processes raises concerns about the reliability and trustworthiness of these models, especially when used in critical real-world scenarios.

Explainability refers to the ability to describe how a model arrives at its predictions, whereas interpretability is the extent to which a human can understand the cause of a decision. Both are crucial for creating transparent AI systems that instill confidence in users. Mathematically, the objective of interpretability can be understood as decomposing the prediction $\hat{y} = f(x)$, where $f(x)$ is a complex machine learning model, into simpler, understandable components. The challenge in AutoML lies in the fact that it often generates highly complex models, such as deep neural networks or ensemble methods like random forests or gradient-boosted trees. These models typically involve thousands or even millions of parameters, making it difficult to trace the influence of individual features on the final predictions.

To illustrate the complexity, consider a deep learning model where the output $\hat{y}$ is a function of multiple layers of parameters and nonlinear activation functions. For such a model, explaining $\hat{y} = f(x_1, x_2, \dots, x_n)$, where $x_1, x_2, \dots, x_n$ represent the input features, involves tracing how each input influences the final output through a series of transformations that are not easily interpretable by a human. In such cases, the interpretability of the model suffers, making it difficult for end users to trust its predictions.

Various methods have been developed to enhance the interpretability of complex models. One of the most prominent techniques is SHapley Additive exPlanations (SHAP), which is grounded in cooperative game theory. SHAP values provide a consistent and theoretically sound approach to calculating feature importance by quantifying the contribution of each feature to the prediction. Mathematically, the SHAP value for feature $x_i$ in a prediction is computed by considering all possible subsets of features and calculating how much $x_i$ contributes to the change in the model's output when added to these subsets. Let $N$ be the set of all features, and let $S \subseteq N \setminus \{i\}$ be any subset of features that does not include $x_i$. The SHAP value $\phi_i(f, x)$ for feature $x_i$ is given by:

$$ \phi_i(f, x) = \sum_{S \subseteq N \setminus \{i\}} \frac{|S|! (|N| - |S| - 1)!}{|N|!} \left( f(S \cup \{i\}) - f(S) \right), $$

where $f(S)$ is the model's prediction using the features in subset $S$. This formulation ensures that each feature's contribution is fairly accounted for by averaging over all possible feature combinations. SHAP values are particularly powerful because they offer a global perspective on model behavior, enabling users to understand the overall importance of features, as well as providing local explanations for individual predictions.

Another widely used technique for enhancing model interpretability is LIME (Local Interpretable Model-agnostic Explanations). Unlike SHAP, which provides a global measure of feature importance, LIME focuses on explaining individual predictions by approximating the complex model $f(x)$ with a simpler, interpretable model $g(x)$ in the local vicinity of the instance being explained. Mathematically, LIME fits the surrogate model $g(x)$, typically a linear model or decision tree, to mimic the behavior of $f(x)$ in a small neighborhood around the instance $x_0$ by minimizing a weighted loss function:

$$ \arg \min_{g \in G} \sum_{x' \in X} \pi(x_0, x') (f(x') - g(x'))^2 + \Omega(g), $$

where $\pi(x_0, x')$ is a proximity measure that assigns higher weights to instances $x'$ closer to $x_0$, and $\Omega(g)$ is a regularization term that ensures the complexity of $g(x)$ remains low. By focusing on local fidelity, LIME enables users to gain insight into how the model makes predictions for specific instances without needing to understand the global complexity of $f(x)$.

These explainability techniques address the primary challenge of interpreting complex machine learning models, particularly those generated by AutoML systems. As AutoML evolves, ensuring that the models it produces are interpretable remains crucial, especially in domains where transparency is essential, such as healthcare, finance, and legal systems. For instance, in healthcare, a model that predicts the likelihood of patient readmission based on various health indicators must provide interpretable explanations for its predictions to be trusted by medical professionals. SHAP and LIME enable practitioners to identify which features, such as age, comorbidities, or recent treatments, contribute the most to the model’s decision, fostering greater trust in the system.

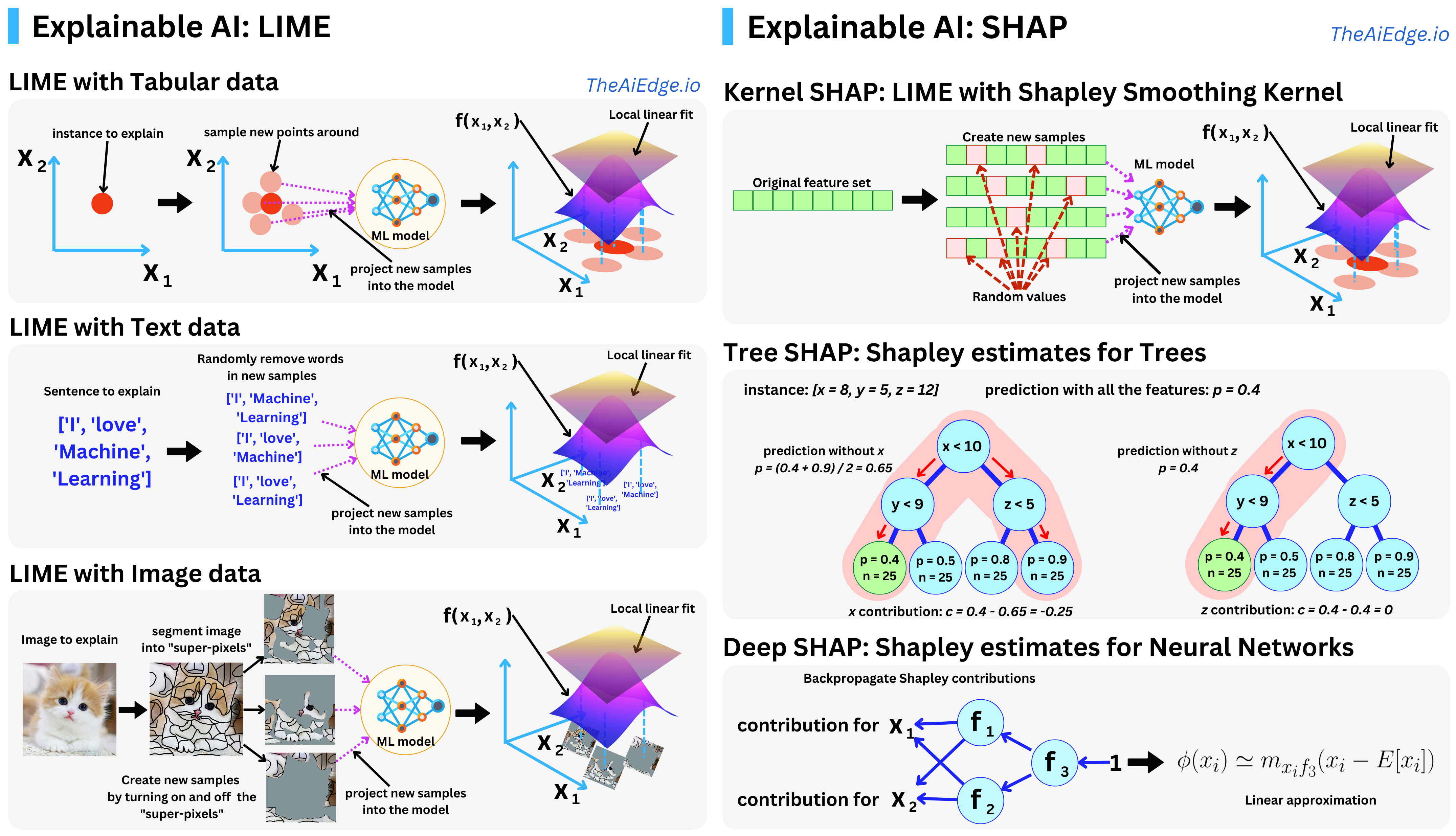
Figure 5: Illustration of SHAP and LIME methods.

The implementation of these techniques in Rust, using libraries such as ndarray and machine learning frameworks like linfa, is feasible and offers performance benefits. Rust's concurrency model and memory safety features are well-suited for implementing computationally intensive tasks like calculating SHAP values across large datasets or training multiple local surrogate models for LIME. Additionally, Rust's parallelism capabilities can be leveraged to speed up these explainability techniques, particularly when dealing with complex models or large-scale datasets.

In conclusion, explainability and interpretability are integral to ensuring that the models generated by AutoML systems are transparent, trustworthy, and useful for end users. As machine learning models become more complex, particularly with the advent of deep learning and ensemble methods, techniques like SHAP and LIME provide valuable tools for making these models more understandable. Implementing these techniques in Rust, with its high-performance capabilities, allows for efficient computation, enabling AutoML systems to deliver both powerful and interpretable models.

Implementing explainability techniques in Rust requires leveraging available libraries and tools. Although Rust's ecosystem for machine learning is still developing, we can use available crates and manually implement some interpretability methods. For this section, we'll focus on a practical approach to interpretability by examining feature importance in a logistic regression model.

Here’s how you can adjust your code to fit a logistic regression model and examine its predictions:

Ensure you have the following dependencies for numerical computations and machine learning:

[dependencies]
ndarray = "0.15"
ndarray-rand = "0.15"
rand = "0.8"
linfa = "0.7"
linfa-logistic = "0.7"

In the main.rs file, we use the linfa crate to create a logistic regression model, fit it to synthetic data, and then analyze the predictions.

use ndarray::{Array1, Array2};
use rand::Rng;
use linfa::prelude::*;
use linfa_logistic::LogisticRegression;

fn main() {
    let mut rng = rand::thread_rng();

    // Generate synthetic data: 100 samples, 2 features
    let features: Array2<f64> = Array2::from_shape_fn((100, 2), |_| rng.gen_range(0.0..1.0));
    let targets: Array1<u8> = Array1::from_shape_fn(100, |_| rng.gen_range(0..2));

    // Convert data to Dataset
    let dataset = Dataset::new(features.clone(), targets.clone());

    // Initialize and fit a LogisticRegression model
    let model = LogisticRegression::default().fit(&dataset).unwrap();

    // Predict using the model
    let predictions = model.predict(dataset.records());

    // Print predictions
    println!("Predictions: {:?}", predictions);
}

In this example, we generate synthetic data consisting of 100 samples and 2 features. We create Array2 for the features and Array1 for the binary target values. This data is then transformed into a Dataset suitable for the LogisticRegression model.

We initialize and fit a LogisticRegression model using the synthetic dataset. Once the model is trained, we use it to make predictions on the dataset. The predictions are printed out to help understand the model’s outputs.

Although this example focuses on generating predictions from a logistic regression model, it illustrates the process of model fitting and evaluation. For a deeper dive into interpretability, more advanced techniques like examining coefficients or implementing SHAP and LIME would be required, but these are not directly available in the current Rust ecosystem. However, this example serves as a foundation for understanding model outputs and can be extended with additional libraries and methods as the ecosystem evolves.

By including these techniques in your Rust-based AutoML system, you enhance the transparency of your automated models. Even though this example is based on a logistic regression model, the underlying principles of model interpretability can be applied to more complex models and techniques as Rust’s machine learning tools continue to develop. This ensures that your models remain both powerful and understandable, fostering greater trust and usability in automated machine learning applications.

17.7. Evaluating and Deploying AutoML Solutions link

In the rapidly evolving field of machine learning, the automation of model selection and hyperparameter tuning—collectively known as Automated Machine Learning (AutoML)—has gained significant traction. As we delve into evaluating and deploying AutoML solutions, it becomes crucial to establish a comprehensive understanding of the core principles that underpin these processes. This section will explore the fundamental ideas of evaluation metrics, the challenges posed by AutoML models, and the best practices for effective deployment in production environments. We will also provide practical insights into implementing an evaluation and deployment pipeline in Rust, applying these concepts to a real-world scenario.

To begin with, evaluating an AutoML solution necessitates a robust framework for assessing model performance. Key metrics such as accuracy, precision, recall, F1-score, and area under the receiver operating characteristic curve (AUC-ROC) are essential for quantifying a model’s effectiveness. However, it’s not just about finding a model that performs well on training data; the ability of a model to generalize to unseen data is paramount. Cross-validation techniques, such as k-fold cross-validation, enable us to assess a model’s robustness by partitioning the dataset into subsets, training the model on a portion of the data, and validating it on the remaining data. This method helps mitigate issues such as overfitting, where a model performs well on training data but fails to generalize to new inputs.

In addition to performance metrics, scalability is a vital consideration when deploying AutoML solutions. As datasets grow and the complexity of models increases, it is crucial to ensure that the chosen models can handle the scale of data in production. This includes evaluating not only the time taken for model training and inference but also the resource utilization in terms of memory and computational power. Implementing logging and monitoring during the deployment phase can provide insights into the model's performance in real-time, allowing for adjustments or retraining if necessary.

Evaluating AutoML models also presents unique challenges. The automated nature of these models means that they often come with many hyperparameters and configurations, making it difficult to ascertain which settings yield optimal performance. Furthermore, the black-box nature of some machine learning algorithms can obscure the interpretability of the model, complicating the evaluation process. Therefore, it is vital to adopt a systematic approach to benchmarking AutoML solutions, encompassing not only performance metrics but also robustness checks and interpretability assessments.

Once we have established a suitable evaluation framework, the next step is deployment. Deployment of AutoML models into production environments requires careful planning and execution. Best practices include containerizing models using tools like Docker, which ensures consistency across different environments and simplifies the deployment process. Moreover, implementing continuous integration and continuous deployment (CI/CD) pipelines can foster a culture of rapid iteration and improvement, allowing teams to deploy updates and enhancements to their models seamlessly.

Now, let’s turn our attention to a practical example of implementing an evaluation and deployment pipeline for an AutoML solution in Rust. We will utilize the linfa crate, which provides a collection of machine learning algorithms and tools in Rust, to demonstrate how to evaluate and deploy a model. In this example, we will build a simple classification model on a synthetic dataset, evaluate its performance, and prepare it for deployment.

First, we need to create a synthetic dataset and train a Decision Tree model using Rust. Below is a sample code snippet that demonstrates this process:

use ndarray::{Array, Array1, Array2, Axis};
use rand::Rng;
use linfa::prelude::*;
use linfa_trees::DecisionTree;
use linfa::Dataset;

fn main() {
    // Create a synthetic dataset
    let mut rng = rand::thread_rng();
    let features: Array2<f32> = Array::from_shape_fn((100, 2), |_| rng.gen_range(0.0..1.0));
    let labels: Array1<usize> = features
        .axis_iter(Axis(0))
        .map(|row| if row.sum() > 1.0 { 1 } else { 0 })
        .collect();

    // Split the dataset into training and testing sets
    let (train_features, test_features) = features.view().split_at(Axis(0), 80);
    let (train_labels, test_labels) = labels.view().split_at(Axis(0), 80);

    // Convert views to owned arrays
    let train_features = Array::from(train_features.to_owned());
    let train_labels = Array::from(train_labels.to_owned());
    let test_features = Array::from(test_features.to_owned());
    let test_labels = Array::from(test_labels.to_owned());

    // Create the Dataset
    let train_dataset = Dataset::new(train_features.clone(), train_labels.clone());

    // Train a Decision Tree model
    let model = DecisionTree::params()
        .fit(&train_dataset)
        .expect("Model training failed");

    // Evaluate the model
    let predictions = model.predict(&test_features);
    let accuracy = calculate_accuracy(&test_labels, &predictions);
    println!("Model accuracy: {:.2}", accuracy);
}

// Function to calculate accuracy
fn calculate_accuracy(true_labels: &Array1<usize>, predictions: &Array1<usize>) -> f64 {
    let correct_count = true_labels.iter().zip(predictions.iter())
        .filter(|&(true_label, pred_label)| true_label == pred_label)
        .count();
    correct_count as f64 / true_labels.len() as f64
}

In this snippet, we generate a synthetic dataset with two features and a binary target variable. We then split the dataset into training and testing sets, train a Decision Tree model on the training set, and evaluate its accuracy on the test set. This example provides a foundational framework for building and evaluating machine learning models, serving as a basic example for an AutoML pipeline.

Next, we will discuss how to deploy the trained model in a production-ready manner. One effective approach is to export the model as a serialized file, which can later be loaded for inference in a web service or another application. Rust provides various serialization libraries, such as serde, to facilitate this process. Below is a code snippet demonstrating how to serialize and deserialize a trained model:

use serde::{Serialize, Deserialize};
use std::fs::File;
use std::io;

#[derive(Serialize, Deserialize)]
struct SerializableModel {
    // Model parameters go here
}

fn save_model(model: &SerializableModel, path: &str) -> io::Result<()> {
    let file = File::create(path)?;
    serde_json::to_writer(file, model)?;
    Ok(())
}

fn load_model(path: &str) -> io::Result<SerializableModel> {
    let file = File::open(path)?;
    let model = serde_json::from_reader(file)?;
    Ok(model)
}

fn main() {
    let model = SerializableModel {
        // Initialize model parameters
    };
    save_model(&model, "model.json").expect("Failed to save model");
    let _loaded_model = load_model("model.json").expect("Failed to load model");
}

In this code, we define a simple structure for a serializable model, including methods to save and load the model using JSON serialization. By employing this approach, we can effectively manage model persistence and facilitate seamless transitions between training and deployment stages.

In conclusion, evaluating and deploying AutoML solutions is a multifaceted challenge that requires a well-defined strategy encompassing performance metrics, robustness, scalability, and best practices for deployment. By leveraging Rust’s powerful ecosystem, we can build efficient and reliable AutoML pipelines that are not only effective in producing high-quality models but also well-equipped for deployment in real-world applications. As we continue to explore the capabilities of AutoML in Rust, we can further enhance our understanding and implementation of these critical processes, ensuring that our solutions are robust, scalable, and capable of driving meaningful insights from data.

17.8. Conclusion link

Chapter 17 equips you with a deep understanding of AutoML and its implementation in Rust. By mastering these techniques, you will be able to automate the machine learning process, enabling you to build and optimize models more efficiently and effectively, while ensuring they remain interpretable and robust.

17.8.1. Further Learning with GenAI link

By exploring these questions, you will deepen your knowledge of the theoretical foundations, key components, and advanced techniques in AutoML, preparing you to build and deploy automated machine learning solutions.

• Explain the fundamental concept of AutoML. What are the primary goals of AutoML, and how does it address the challenges of traditional machine learning workflows? Implement a basic AutoML pipeline in Rust.

• Discuss the role of feature engineering in machine learning. Why is feature engineering crucial for model performance, and what are the challenges of automating this process? Implement automated feature engineering in Rust and evaluate its impact on model accuracy.

• Analyze the impact of model selection and hyperparameter tuning in AutoML. How do these processes optimize model performance, and what strategies are commonly used for automation? Implement automated model selection and hyperparameter tuning in Rust.

• Explore the concept of Neural Architecture Search (NAS). How does NAS automate the design of neural network architectures, and what are the trade-offs between search space size and computational efficiency? Implement a NAS algorithm in Rust and apply it to a neural network task.

• Discuss the principles of meta-learning in the context of AutoML. How does meta-learning enable models to learn from previous experiences, and what are the benefits of applying it to automated machine learning tasks? Implement meta-learning techniques in Rust for a dataset with limited data.

• Analyze the role of transfer learning in AutoML. How does transfer learning leverage pre-trained models or knowledge from related tasks, and what are the challenges of applying it to new tasks? Implement transfer learning in Rust and apply it to a real-world problem.

• Explore the importance of explainability and interpretability in AutoML. Why is it crucial for automated models to be understandable and transparent, and what techniques can be used to improve interpretability? Implement explainability techniques in Rust for an AutoML-generated model.

• Discuss the challenges of evaluating AutoML models. What metrics are used to assess model performance and robustness, and how can these be applied to automated solutions? Implement an evaluation pipeline in Rust for an AutoML model and analyze the results.

• Analyze the process of deploying AutoML solutions in production. What are the key considerations for scaling and maintaining automated models, and what best practices should be followed? Implement a deployment pipeline in Rust for an AutoML solution and evaluate its scalability.

• Explore the concept of hyperparameter optimization in AutoML. How does hyperparameter optimization enhance model performance, and what are the different approaches used in AutoML for tuning hyperparameters? Implement hyperparameter optimization in Rust and apply it to a complex model.

• Discuss the trade-offs between automation and control in AutoML. How does AutoML balance the need for automation with the desire for model customization and control, and what are the implications for model performance? Implement a customizable AutoML pipeline in Rust and evaluate its flexibility.

• Analyze the use of Bayesian optimization in AutoML. How does Bayesian optimization improve the efficiency of hyperparameter tuning, and what are its advantages over other optimization methods? Implement Bayesian optimization in Rust and apply it to a hyperparameter tuning task.

• Explore the role of ensembling in AutoML. How does AutoML utilize ensemble methods to improve model performance, and what are the challenges of automating ensemble creation? Implement an ensemble method in Rust within an AutoML pipeline and evaluate its impact on model accuracy.

• Discuss the application of AutoML in different domains. How can AutoML be adapted to specific industries, such as healthcare, finance, or marketing, and what are the unique challenges in each domain? Implement an AutoML solution in Rust tailored to a specific industry and evaluate its effectiveness.

• Analyze the impact of data preprocessing in AutoML. How does AutoML handle data preprocessing, such as missing data imputation and normalization, and what are the best practices for automating these steps? Implement automated data preprocessing in Rust and apply it to a noisy dataset.

• Explore the future directions of research in AutoML. What are the emerging trends and challenges in the field of AutoML, and how can advances in machine learning and AI contribute to the development of more powerful and efficient automated systems? Implement a cutting-edge AutoML technique in Rust and experiment with its application to a real-world problem.

• Discuss the ethical considerations in AutoML. How does the automation of machine learning impact issues like fairness, bias, and transparency, and what steps can be taken to ensure ethical practices in AutoML? Implement a fairness-aware AutoML pipeline in Rust and evaluate its impact on model decisions.

• Analyze the concept of AutoML for deep learning. How does AutoML extend to deep learning models, such as convolutional neural networks and recurrent neural networks, and what are the challenges of automating deep learning? Implement an AutoML solution in Rust for a deep learning task and evaluate its performance.

• Explore the role of reinforcement learning in AutoML. How can reinforcement learning be applied to optimize AutoML pipelines, and what are the benefits of using it for automated machine learning tasks? Implement a reinforcement learning-based AutoML solution in Rust and apply it to a complex problem.

By engaging with these questions, you will explore the theoretical foundations, key components, and advanced techniques in AutoML, enabling you to build and deploy automated machine learning solutions with confidence.

17.8.2. Hands On Practices link

By completing these tasks, you will gain hands-on experience with AutoML, deepening your understanding of its implementation and application in machine learning.