18.1 Introduction to Data Processing link

Data processing is a foundational step in the machine learning pipeline, as it plays a critical role in determining the quality and suitability of the input data used to train models. The transformation of raw data into a structured and analyzable format is crucial to ensure that machine learning algorithms can effectively learn patterns and generalize from the data. The significance of this process cannot be overstated: without rigorous data processing, even the most advanced algorithms can yield poor or misleading results, as they are sensitive to inconsistencies, noise, or improper formatting within the input data. Consequently, data processing serves as the backbone of the entire machine learning workflow, ensuring that the data used for training is both accurate and representative of the phenomena the model is designed to predict.

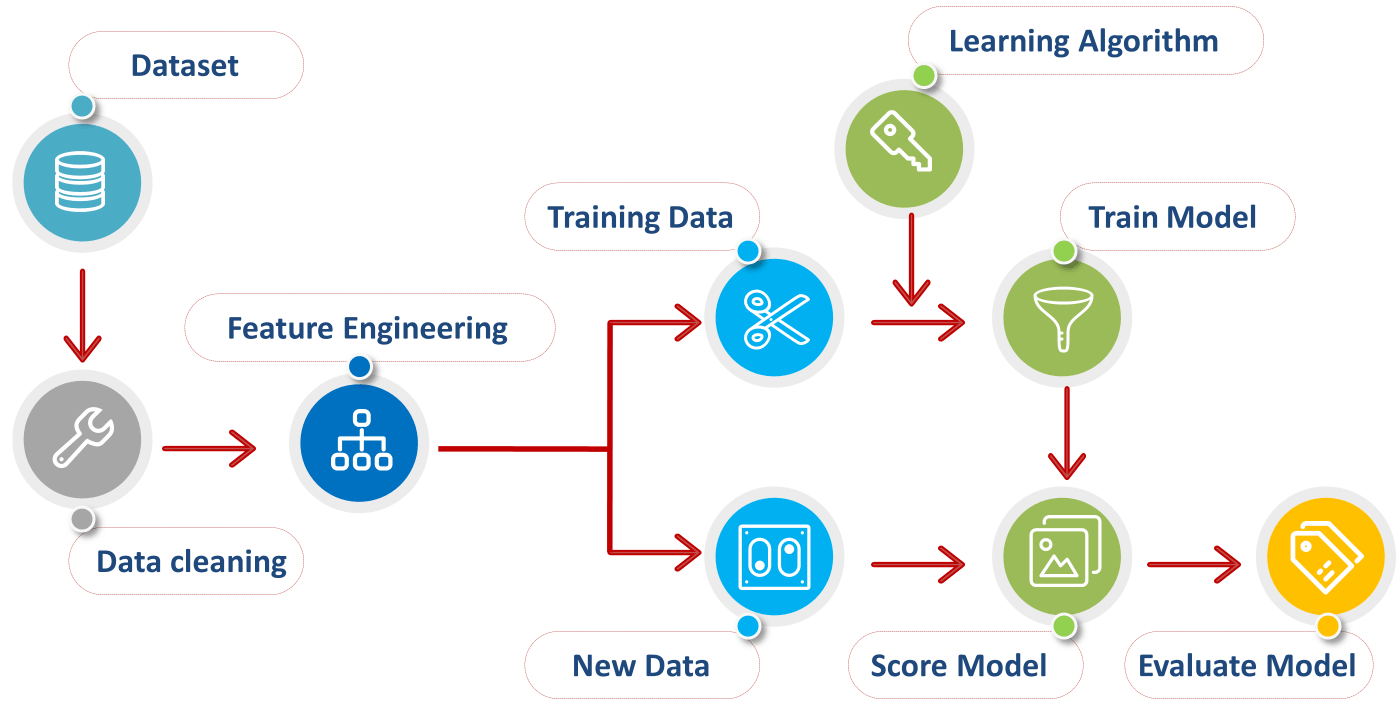
Figure 1: Data processing flow for machine learning.

At a formal level, the process of data preparation involves multiple steps, each of which is guided by the nature of the data itself. To begin with, data types must be considered, as they inform the preprocessing techniques needed. Data encountered in machine learning can be broadly categorized into numerical, categorical, ordinal, or more complex forms such as time series or text data. Each data type presents its own challenges and requires specific transformations to make it suitable for use in machine learning algorithms.

For numerical data, preprocessing often involves normalization or standardization. Let $X \in \mathbb{R}^{n \times d}$ be a dataset consisting of nnn samples and $d$ features, where each feature $X_j$ is a column vector. In cases where the numerical features differ in scale, normalization or standardization is used to prevent certain features from dominating the learning process. Standardization transforms a feature $X_j$ by centering it around zero with unit variance, and is defined mathematically as:

$$ X_j' = \frac{X_j - \mu_j}{\sigma_j}, $$

where $\mu_j$ is the mean of feature $X_j$ and $\sigma_j$ is its standard deviation. Normalization, on the other hand, scales each feature to a specific range, typically between 0 and 1, using the transformation:

$$ X_j' = \frac{X_j - \min(X_j)}{\max(X_j) - \min(X_j)}. $$

The choice between normalization and standardization depends on the characteristics of the data and the model being used. For instance, models such as k-nearest neighbors (KNN) or support vector machines (SVMs) are particularly sensitive to feature scales, making normalization or standardization critical.

For categorical data, preprocessing involves encoding the data into a numerical format that machine learning algorithms can interpret. Categorical features are variables that take on a limited number of discrete values, such as colors, product categories, or labels. One common encoding technique is one-hot encoding, which transforms a categorical variable into a binary vector. For a categorical feature $C$ with $k$ possible categories, one-hot encoding produces a matrix $O \in \mathbb{R}^{n \times k}$, where each row corresponds to a sample, and each column represents a binary indicator for a specific category. This encoding allows models to interpret categorical distinctions without imposing ordinal relationships where none exist.

For example, if $C$ can take values from the set $\{A, B, C\}$, one-hot encoding would transform $C$ into:

$$\text{One-hot encoding of } C = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$$

Another approach for handling categorical data is target encoding, which replaces each category with the mean target value for that category from the training data. This method can be effective when dealing with high-cardinality categorical features, but it must be applied with caution, as it may lead to data leakage if not handled correctly during cross-validation.

Handling missing data is another key aspect of data processing. Missing values occur frequently in real-world datasets and can adversely affect the performance of machine learning models if not addressed properly. Formally, let $\mathcal{D} = \{(x_i, y_i)\}_{i=1}^n$ represent a dataset, where $x_i$ is the feature vector for sample $i$ and $y_i$ is its corresponding target value. If some components of $x_i$ are missing, denoted as $x_i^{(j)} = \text{NaN}$, several strategies can be employed to manage these missing values.

One common strategy is imputation, where missing values are replaced with estimates based on the available data. A simple form of imputation involves replacing missing values with the mean (for numerical data) or the mode (for categorical data). Formally, for a feature $X_j$ with missing values, the mean imputation is expressed as:

$$ x_i^{(j)} = \mu_j \quad \text{for all } x_i^{(j)} = \text{NaN}, $$

where $\mu_j$ is the mean of the non-missing values in feature $X_j$. More advanced imputation methods involve using machine learning models to predict missing values based on other features, such as k-nearest neighbors imputation or regression-based imputation.

Alternatively, missing data can be handled by removing instances with missing values, though this may lead to a loss of valuable information if a significant portion of the dataset is incomplete. In practice, the decision to impute or remove missing values depends on the extent and pattern of missingness in the data. If missingness is random (i.e., missing completely at random), imputation is typically preferred, as removing instances may unnecessarily reduce the dataset size.

The importance of high-quality data processing becomes evident when considering its direct impact on model performance. Poorly processed data can introduce noise, biases, or inconsistencies into the model training process, potentially leading to overfitting, underfitting, or unreliable predictions. Overfitting occurs when the model captures noise or irrelevant patterns in the training data, making it overly complex and reducing its ability to generalize to unseen data. Underfitting, on the other hand, occurs when the model is too simplistic to capture the underlying structure of the data, leading to poor performance on both training and validation datasets. Effective data processing mitigates these risks by ensuring that the input data is clean, well-structured, and representative of the task at hand.

In practical implementations using Rust, data processing can be efficiently handled with libraries such as ndarray for numerical arrays, csv for handling data files, and serde for serialization. Rust’s performance-oriented design makes it well-suited for large-scale data processing tasks, particularly when working with high-dimensional datasets or large volumes of data. The combination of Rust’s type safety, memory management, and concurrency features allows for the development of robust and scalable data processing pipelines that can seamlessly integrate with machine learning workflows.

In conclusion, data processing is a critical step in the machine learning workflow that directly influences the quality and effectiveness of the models built from the data. By addressing key challenges such as normalization, categorical encoding, and handling missing values, data processing ensures that machine learning models are trained on well-prepared and representative data. Implementing these techniques efficiently in Rust, with its high-performance capabilities, allows for the development of scalable and reliable machine learning applications that can handle complex data processing tasks with ease.

To illustrate these concepts, let’s consider a simple example in Rust where we have a dataset represented as a vector of tuples. Each tuple contains a numeric feature and a categorical feature. We will handle missing values, normalize the numeric feature, and encode the categorical feature for further analysis.

First, let’s define our dataset:

fn main() {
    let data: Vec<Option<(f64, &str)>> = vec![
        Some((1.0, "A")),
        Some((2.5, "B")),
        None,
        Some((4.0, "A")),
        Some((5.5, "C")),
        None,
    ];
    println!("Original Data: {:?}", data);
}

In this dataset, we have some missing values represented as None. The first step in our data processing journey is to handle these missing values. Here, we can opt to replace the missing values with the mean of the available entries.

fn handle_missing_values(data: Vec<Option<(f64, &str)>>) -> Vec<(f64, &str)> {
    let sum: f64 = data.iter()
        .filter_map(|x| x.as_ref())
        .map(|(num, _)| num)
        .sum();
    
    let count = data.iter().filter(|x| x.is_some()).count();
    let mean = sum / count as f64;

    data.into_iter()
        .map(|opt| match opt {
            Some(value) => value,
            None => (mean, "Unknown"),
        })
        .collect()
}

fn main() {
    let data = vec![
        Some((1.0, "A")),
        Some((2.5, "B")),
        None,
        Some((4.0, "A")),
        Some((5.5, "C")),
        None,
    ];
    let processed_data = handle_missing_values(data);
    println!("Processed Data: {:?}", processed_data);
}

In the above code, we define a function handle_missing_values that calculates the mean of the numeric values and replaces any missing values with this mean. This allows us to retain the dimensionality of our dataset while ensuring that our model can still learn from it.

Next, we will normalize the numeric feature to ensure that it falls within a specific range. Normalization is crucial as it helps in speeding up the convergence of optimization algorithms.

fn normalize_features(data: &mut Vec<(f64, &str)>) {
    let max_value = data.iter().map(|(num, _)| num).cloned().fold(f64::NAN, f64::max);
    let min_value = data.iter().map(|(num, _)| num).cloned().fold(f64::NAN, f64::min);

    for (num, cat) in data.iter_mut() {
        *num = (*num - min_value) / (max_value - min_value);
    }
}

fn main() {
  	let data = vec![
        Some((1.0, "A")),
        Some((2.5, "B")),
        None,
        Some((4.0, "A")),
        Some((5.5, "C")),
        None,
    ];
    let mut processed_data = handle_missing_values(data);
    normalize_features(&mut processed_data);
    println!("Normalized Data: {:?}", processed_data);
}

In the normalize_features function, we first compute the maximum and minimum values of the numeric features, then apply min-max normalization to scale each feature between 0 and 1. This is essential for many machine learning algorithms, as it ensures that they treat each feature equally regardless of its original scale.

Finally, we need to encode our categorical feature. One common approach is to use one-hot encoding, which creates new binary features for each category.

use std::collections::HashSet;

fn one_hot_encode(data: &[(f64, &str)]) -> Vec<Vec<f64>> {
    let mut categories = HashSet::new();
    for &(_, cat) in data {
        categories.insert(cat);
    }
  
    let mut encoded_data: Vec<Vec<f64>> = Vec::with_capacity(data.len());
    for &(num, cat) in data {
        let mut one_hot = vec![0.0; categories.len()];
        let index = categories.iter().position(|&c| c == cat).unwrap();
        one_hot[index] = 1.0;
        let mut row = vec![num];
        row.extend(one_hot);
        encoded_data.push(row);
    }
    encoded_data
}

fn main() {
  	let data = vec![
        Some((1.0, "A")),
        Some((2.5, "B")),
        None,
        Some((4.0, "A")),
        Some((5.5, "C")),
        None,
    ];
    let mut processed_data = handle_missing_values(data);
    normalize_features(&mut processed_data);
    let encoded_data = one_hot_encode(&processed_data);
    println!("One-Hot Encoded Data: {:?}", encoded_data);
}

In the one_hot_encode function, we first compile a set of unique categories from the data, then iterate through each entry to create a new vector that combines the normalized numeric value with the one-hot encoded binary values for the categorical feature. The resulting structure is a two-dimensional vector where each row corresponds to an input sample, with the first element being the normalized numeric feature and the subsequent elements representing the one-hot encoded categories.

In conclusion, data processing is a foundational element of machine learning that ensures the data used for training models is clean, well-structured, and relevant. By understanding and implementing techniques such as handling missing values, normalizing features, and encoding categorical variables in Rust, we can significantly enhance the quality of our datasets. This ultimately leads to more reliable and effective machine learning models that can generalize well to new data. As we proceed through this chapter, we will delve deeper into these techniques and explore more advanced data processing methods that are essential for successful machine learning applications.

18.2. Data Cleaning and Preprocessing link

Data cleaning and preprocessing form the foundation of any machine learning workflow, as they directly influence the quality of the input data, which in turn affects model performance and accuracy. Without proper data cleaning, even the most advanced machine learning models can yield unreliable results. This section delves into the key concepts of data cleaning, examines the consequences of noisy and inconsistent data, and explores practical methods for implementing various data cleaning techniques using Rust. The ultimate goal is to provide a comprehensive understanding of how to effectively prepare data for machine learning tasks.

One of the initial steps in data cleaning involves detecting and handling outliers—data points that deviate significantly from the rest of the dataset. Outliers can arise for several reasons, including measurement errors, data entry mistakes, or legitimate rare events that exhibit true variability in the data. Regardless of their origin, outliers can skew statistical analyses and compromise the accuracy of machine learning models. Consequently, it is crucial to identify these outliers and apply appropriate methods to address them, depending on whether the outliers represent erroneous data or meaningful variability.

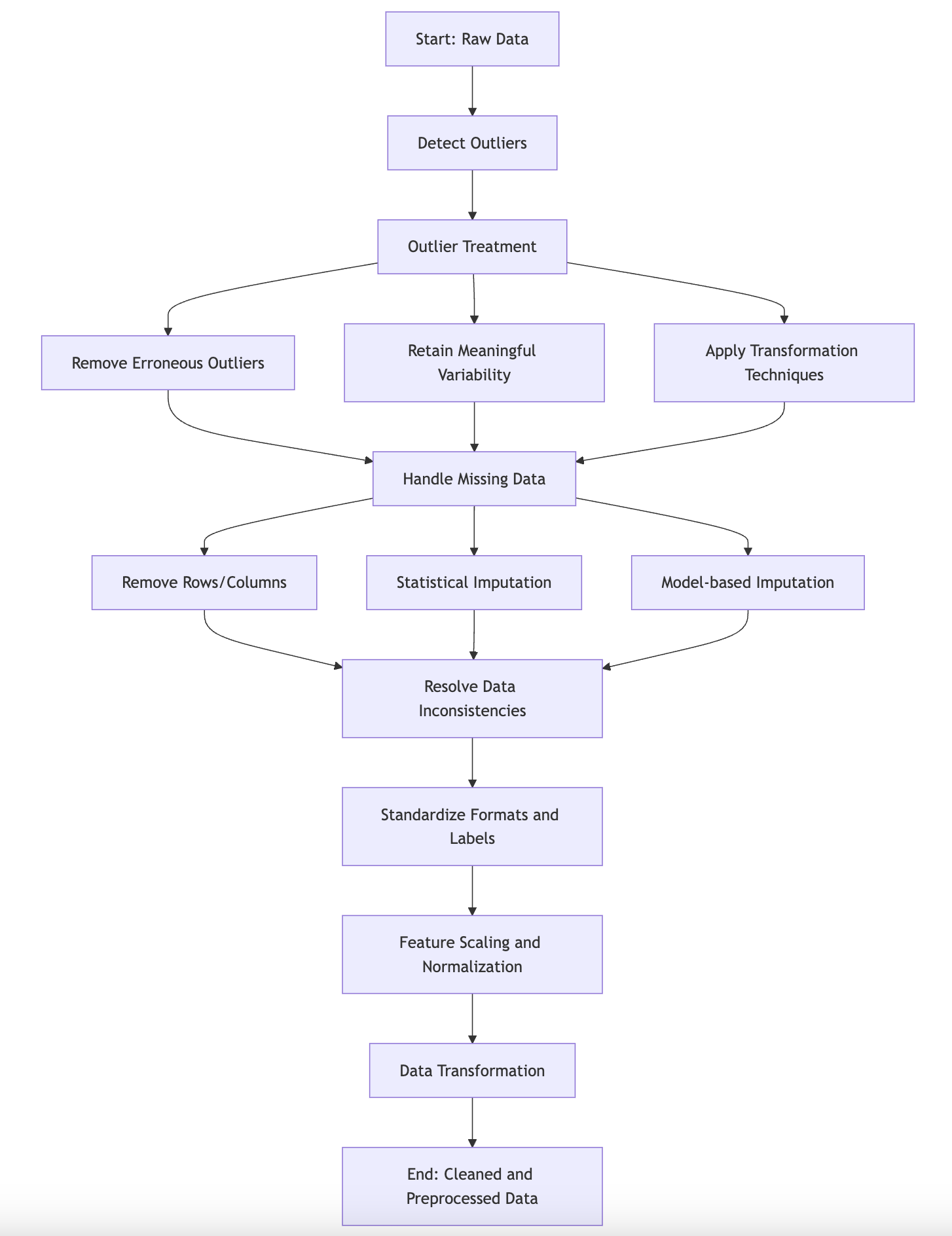
Figure 2: Illustration of data preprocessing and cleaning.

Mathematically, an outlier can be defined as a data point that lies at an abnormal distance from other values in a given distribution. Two commonly used methods for outlier detection are the Z-score method and the Interquartile Range (IQR) method. These methods provide formal approaches to quantifying whether a data point should be considered an outlier.

The Z-score method is based on the assumption that the data follows a Gaussian (normal) distribution. In this method, the Z-score of each data point is computed, which measures how many standard deviations away the data point is from the mean of the distribution. Let $x$ be a data point in a dataset $X$ with mean $\mu$ and standard deviation $\sigma$. The Z-score $Z$ of $x$ is defined as:

$$ Z = \frac{x - \mu}{\sigma}. $$

If the Z-score of a data point exceeds a certain threshold—commonly 3 or -3—then the data point is considered an outlier. This threshold is chosen based on the properties of the normal distribution, where approximately 99.7% of data points fall within three standard deviations of the mean. Therefore, data points with Z-scores beyond this range are deemed unusually distant from the rest of the data.

However, the Z-score method assumes that the data is normally distributed. In cases where the data does not conform to a Gaussian distribution, the Interquartile Range (IQR) method provides an alternative approach. The IQR is a measure of statistical dispersion, defined as the difference between the third quartile (Q3) and the first quartile (Q1) of the data. Formally:

$$ \text{IQR} = Q3 - Q1. $$

The IQR method identifies outliers by considering data points that fall outside a certain range relative to the IQR. Specifically, any data point $x$ that satisfies one of the following conditions is considered an outlier:

$$x < Q1 - 1.5 \times \text{IQR} \quad \text{or} \quad x>Q1+1.5 \times \text{IQR} $$

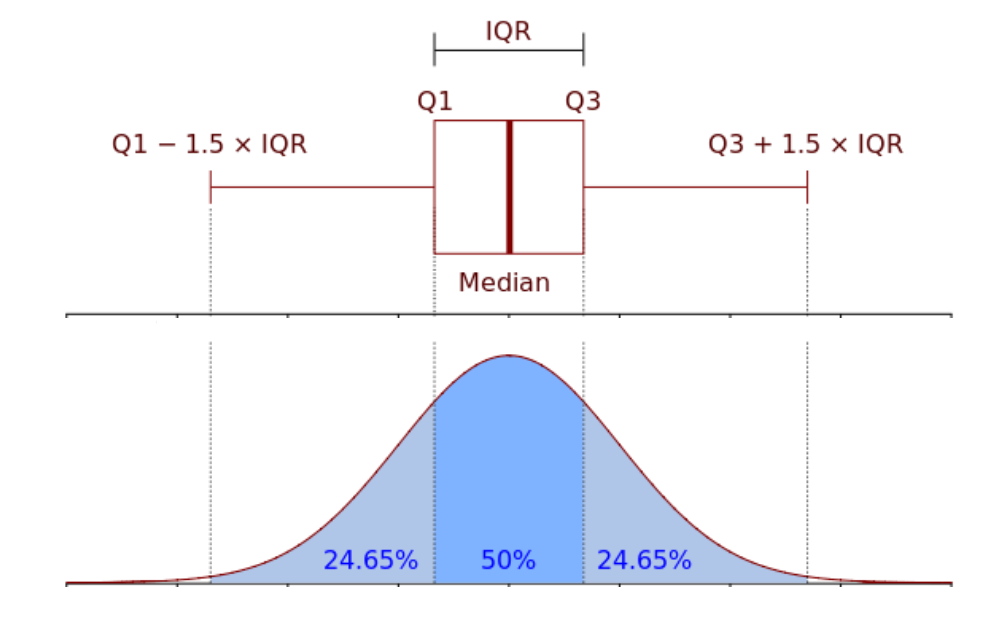
Figure 3: Illustration of IQR method.

This approach is particularly useful for non-parametric data distributions, where the assumption of normality does not hold. It is also robust to extreme values, as it relies on the median and quartiles, which are less sensitive to outliers than the mean and standard deviation.

Once outliers have been identified using these methods, the next challenge is deciding how to handle them. There are several strategies available for addressing outliers, depending on the nature of the data and the desired outcome. One common approach is removal, where outliers are simply excluded from the dataset. This method is appropriate when outliers are deemed to be erroneous or irrelevant. However, in cases where outliers represent legitimate but rare events, removal may result in the loss of valuable information.

Another approach is imputation, where outliers are replaced with more representative values, such as the median or the mean of the remaining data. This method is less aggressive than removal and can help preserve the overall structure of the data. In some cases, transformation techniques, such as logarithmic scaling or square root transformations, are applied to mitigate the influence of outliers by reducing the skewness of the distribution.

In practice, implementing these outlier detection and handling techniques in Rust involves utilizing libraries like ndarray for data manipulation and numerical operations. For example, the Z-score method can be implemented by calculating the mean and standard deviation of a dataset and then iterating over the data points to compute their Z-scores. Similarly, the IQR method can be implemented by sorting the dataset, calculating the quartiles, and identifying data points that fall outside the specified range. The following code snippets illustrate how these methods might be implemented in Rust:

First, we will implement the Z-score method:

fn z_score_outliers(data: &[f64]) -> Vec<f64> {
    let mean = data.iter().copied().sum::<f64>() / data.len() as f64;
    let std_dev = (data.iter().map(|x| (x - mean).powi(2)).sum::<f64>() / data.len() as f64).sqrt();
    
    data.iter()
        .filter(|&&x| (x - mean).abs() > 2.0 * std_dev)
        .copied()
        .collect()
}

fn main() {
    let data = vec![1.0, 2.0, 3.0, 4.0, 5.0, 100.0];
    let outliers = z_score_outliers(&data);
    if outliers.is_empty() {
        println!("No outliers found.");
    } else {
        for outlier in outliers {
            println!("{}", outlier);
        }
    }
}

Now, let's implement the IQR method:

fn iqr_outliers(data: &[f64]) -> Vec<f64> {
    let mut sorted_data = data.to_vec();
    sorted_data.sort_by(|a, b| a.partial_cmp(b).unwrap());
    
    let q1 = sorted_data[sorted_data.len() / 4];
    let q3 = sorted_data[3 * sorted_data.len() / 4];
    let iqr = q3 - q1;

    let lower_bound = q1 - 1.5 * iqr;
    let upper_bound = q3 + 1.5 * iqr;

    sorted_data.iter()
        .filter(|&&x| x < lower_bound || x > upper_bound)
        .copied()
        .collect()
}

fn main() {
    let data = vec![1.0, 2.0, 3.0, 4.0, 5.0, 100.0];
    let outliers = iqr_outliers(&data);
    if outliers.is_empty() {
        println!("No outliers found.");
    } else {
        for outlier in outliers {
            println!("{}", outlier);
        }
    }
}

The next critical aspect of data cleaning is dealing with noise in the dataset. Noise refers to random errors or variances in measured variables, which can obscure the true signal in the data. Noise can be reduced using several techniques, such as smoothing methods, which might include moving averages or more sophisticated techniques like Gaussian filtering.

For instance, we can implement a simple moving average in Rust as follows:

fn moving_average(data: &[f64], window_size: usize) -> Vec<f64> {
    let mut averages = Vec::new();
    for i in 0..data.len() {
        if i + window_size <= data.len() {
            let window: Vec<f64> = data[i..i + window_size].to_vec();
            let average: f64 = window.iter().copied().sum::<f64>() / window.len() as f64;
            averages.push(average);
        }
    }
    averages
}

fn main() {
    let data = vec![1.0, 2.0, 3.0, 4.0, 5.0];
    let window_size = 3;
    let result = moving_average(&data, window_size);
    for value in result {
        println!("{:.2}", value);
    }
}

The final layer of data cleaning involves correcting inconsistencies within the data, which can arise from various sources. For instance, categorical variables may have different representations for the same category, such as "yes" and "Yes". Addressing these issues through standardized formats is vital for ensuring the integrity of the data.

Data imputation is another significant part of preprocessing, especially in cases where missing values are present. Simple strategies for data imputation include replacing missing values with the mean, median, or mode of the respective feature. A more sophisticated approach might involve predicting missing values based on other available data. Below is an example of how to implement mean imputation in Rust:

fn mean_imputation(data: &mut Vec<Option<f64>>) {
    let sum: f64 = data.iter().filter_map(|&x| x).sum();
    let count = data.iter().filter(|&&x| x.is_some()).count();
    let mean = sum / count as f64;

    for value in data.iter_mut() {
        if value.is_none() {
            *value = Some(mean);
        }
    }
}

fn main() {
    let mut data = vec![Some(1.0), None, Some(3.0), None, Some(5.0)];
    mean_imputation(&mut data);
    println!("{:?}", data);
}

In conclusion, data cleaning and preprocessing are foundational steps in the machine learning lifecycle. By effectively identifying and handling outliers, reducing noise, correcting inconsistencies, and implementing robust data imputation strategies, we can ensure that our models are trained on high-quality data. The Rust programming language provides powerful capabilities for implementing these data cleaning techniques, enabling developers to build efficient and reliable machine learning applications. As we progress in this book, we will continue to explore advanced preprocessing techniques and their applications in the context of machine learning with Rust.

18.3. Data Transformation Techniques link

Data transformation is a critical stage in the machine learning pipeline that bridges raw data with machine learning algorithms, enabling the latter to effectively interpret and utilize the data. Transforming data into a more structured and analyzable form often involves scaling, encoding, and binning—techniques that reshape the values, structure, or format of the data to align with the specific requirements of machine learning models. These techniques address the potential issues posed by raw data, such as variations in scale, non-numerical data, and the need to simplify complex relationships. In this section, we delve into the formal principles of these techniques and explore how to implement them practically using Rust.

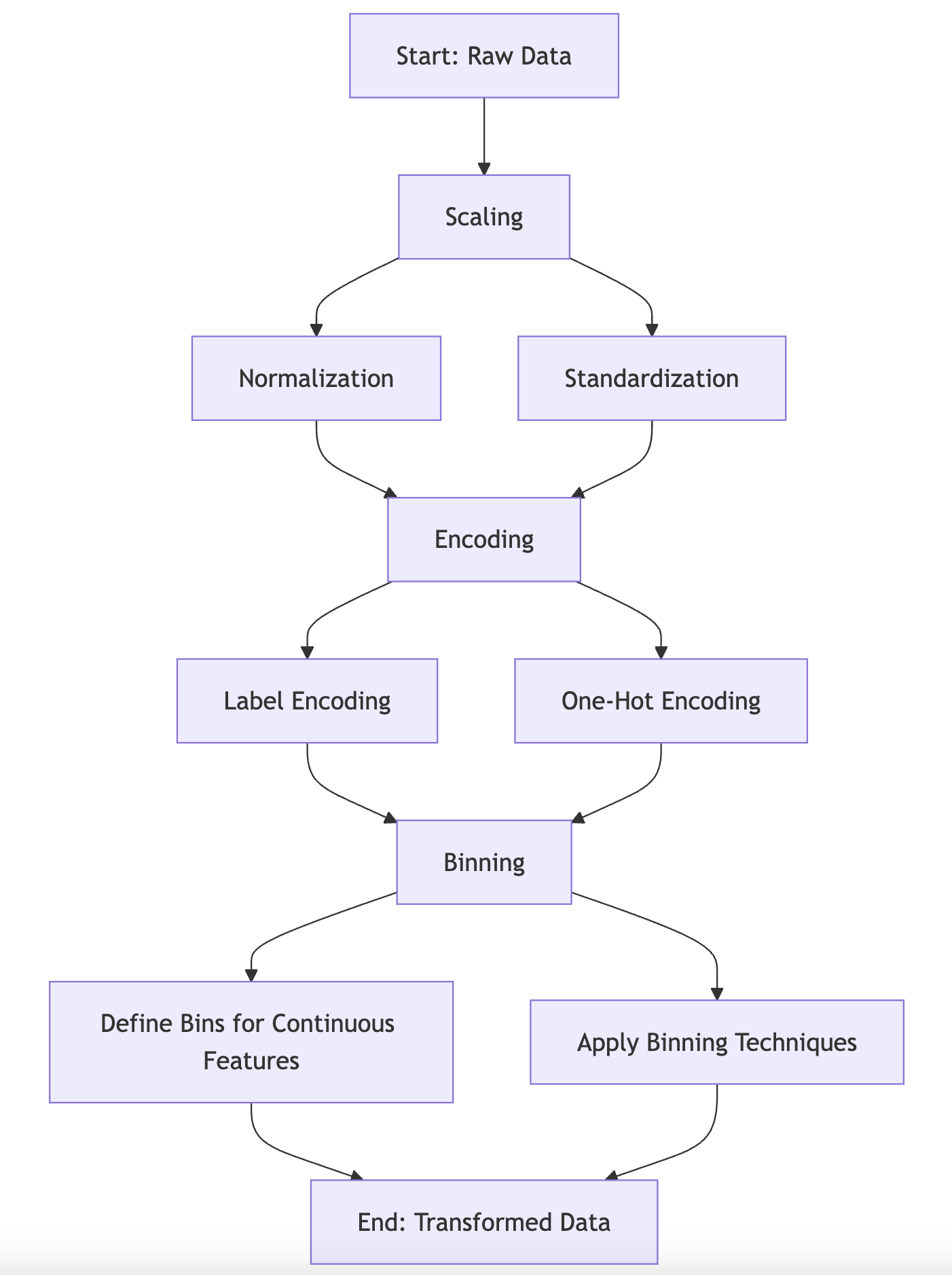
Figure 4: Illustration of data transformation.

At the heart of data transformation is scaling, a process that adjusts the range and distribution of numerical values to ensure that features contribute equally to the learning process. Consider the importance of scaling in algorithms like gradient descent or distance-based models, where the magnitude of features can significantly influence the results. For instance, in k-nearest neighbors (KNN), the distance between data points is computed using a metric like Euclidean distance. If one feature, such as income, ranges from 20,000 to 200,000 while another feature, such as age, ranges from 0 to 100, the income feature will disproportionately dominate the distance calculations, leading to biased predictions. This issue is rectified by scaling the features to a comparable range.

Two common scaling techniques are min-max scaling and standardization. Min-max scaling transforms the data to fit within a specified range, typically \[0, 1\]. For a feature XXX with minimum value $X_{\min}$ and maximum value $X_{\max}$, min-max scaling is defined mathematically as:

$$ X' = \frac{X - X_{\min}}{X_{\max} - X_{\min}}, $$

where $X'$ represents the scaled feature. This transformation ensures that all values of $X$ fall between 0 and 1, which prevents any one feature from disproportionately affecting the model.

Standardization, on the other hand, centers the data around a mean of 0 and scales it according to its standard deviation, effectively converting the data to a distribution with mean 0 and standard deviation 1. Formally, standardization is defined as:

$$ X' = \frac{X - \mu_X}{\sigma_X}, $$

where $\mu_X$ is the mean of the feature and $\sigma_X$ is its standard deviation. Standardization is particularly useful when the data follows a Gaussian distribution or when the features have widely varying scales, as it normalizes the effect of each feature on the model.

The next critical transformation technique is encoding, which converts categorical data into a numerical format that machine learning algorithms can process. Categorical features, such as color (red, blue, green) or product category, cannot be directly used by most algorithms, which require numerical inputs. One common encoding method is one-hot encoding, which transforms a categorical variable with $k$ possible categories into $k$ binary variables, each representing one category. Let $C$ be a categorical variable with values $\{c_1, c_2, \dots, c_k\}$. One-hot encoding represents $C$ by constructing a matrix $O \in \mathbb{R}^{n \times k}$, where $n$ is the number of samples, and each binary column corresponds to one of the $k$ categories. For each observation, the appropriate column takes a value of 1, while the others are set to 0. This encoding ensures that the model does not assume any ordinal relationship between the categories, which could otherwise introduce bias.

Mathematically, if we have a dataset with categorical feature $C \in \{A, B, C\}$, one-hot encoding would transform this feature into three binary columns as follows:

$$ \begin{bmatrix} A \\ B \\ C \end{bmatrix} \rightarrow \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}.​ $$

This transformation ensures that the model treats the categorical values as independent, preventing any misinterpretation of relationships between the categories.

In contrast to encoding techniques for categorical data, binning involves transforming continuous numerical data into discrete intervals or categories. Binning can enhance model interpretability and reduce the sensitivity of the model to minor variations in the data. For example, consider a feature representing age. Rather than using raw age values, we can bin the ages into categories like 'child' (0-12), 'teen' (13-19), 'adult' (20-64), and 'senior' (65+). This reduces the continuous feature space to a smaller set of discrete intervals, which can simplify the model's learning process.

Binning a continuous variable $X$ into $k$ categories involves defining $k-1$ threshold values $\{t_1, t_2, \dots, t_{k-1}\}$, such that each bin corresponds to a range $[t_{i-1}, t_i)$. Formally, binning maps each value $X_i$ to a discrete category:

$$ X_i' = \text{category}_j \quad \text{if} \quad t_{j-1} \leq X_i < t_j. $$

For example, if age is divided into bins representing 'child' (0-12), 'teen' (13-19), 'adult' (20-64), and 'senior' (65+), a person aged 25 would fall into the 'adult' category. Binning is particularly useful in cases where capturing general trends is more important than precise numerical values.

Implementing these transformation techniques in Rust can be efficiently achieved using libraries like ndarray for numerical operations and csv for handling data files. For instance, min-max scaling in Rust can be implemented by iterating over the dataset to compute the minimum and maximum values for each feature, followed by applying the scaling formula to each data point. Similarly, one-hot encoding can be implemented by mapping categorical values to binary vectors and constructing a new dataset with the transformed features.

Moving forward to the practical implementation of these transformation techniques in Rust, we can leverage the ndarray crate, which provides powerful tools for numerical operations. To demonstrate min-max scaling, we can define a function that takes an array of values and scales them to a specified range, typically \[0, 1\]. Here's how we can implement this:

use ndarray::Array1;

fn min_max_scaling(data: &Array1<f64>) -> Array1<f64> {
    let min = data.fold(f64::INFINITY, |a, &b| a.min(b));
    let max = data.fold(f64::NEG_INFINITY, |a, &b| a.max(b));
    let range = max - min;

    data.mapv(|x| (x - min) / range)
}

fn main() {
    let data = Array1::from_vec(vec![10.0, 20.0, 30.0, 40.0, 50.0]);
    let scaled_data = min_max_scaling(&data);
    println!("Scaled Data: {:?}", scaled_data);
}

In this implementation, we compute the minimum and maximum values of the input array, then scale each element to the range \[0, 1\] using the formula (x - min) / (max - min). This simple function effectively transforms the input data while preserving its distribution characteristics.

Next, we will implement one-hot encoding. This can be done by creating a function that generates a binary representation for each category in a given categorical variable. For instance, consider a categorical variable with three distinct categories. Here’s a sample implementation:

use std::collections::HashMap;

fn one_hot_encode(data: &[&str]) -> Vec<Vec<u8>> {
    let unique_categories: Vec<&str> = data.iter().cloned().collect();
    let mut categories_map = HashMap::new();

    for (i, &category) in unique_categories.iter().enumerate() {
        categories_map.insert(category, i);
    }

    data.iter().map(|&category| {
        let mut encoded = vec![0; unique_categories.len()];
        if let Some(&index) = categories_map.get(category) {
            encoded[index] = 1;
        }
        encoded
    }).collect()
}

fn main() {
    let data = vec!["red", "blue", "green", "blue", "red"];
    let encoded_data = one_hot_encode(&data);
    println!("One-hot Encoded Data: {:?}", encoded_data);
}

In this function, we first create a map that associates each unique category with an index. Then, for each entry in the data, we create a binary vector that marks the presence of the category with a 1 at the corresponding index and 0s elsewhere. The output is a two-dimensional vector that represents the one-hot encoded version of the input categorical variable.

Lastly, let’s explore binning continuous variables into categorical intervals. This technique can help us discretize our data, making it easier to analyze and interpret. Below is an example of how we can implement a binning function in Rust:

fn bin_continuous(data: &[f64], bins: &[f64]) -> Vec<usize> {
    data.iter().map(|&value| {
        bins.iter().position(|&bin| value < bin).unwrap_or(bins.len())
    }).collect()
}

fn main() {
    let data = vec![2.5, 3.6, 7.8, 8.1, 10.0];
    let bins = vec![3.0, 6.0, 9.0, 12.0]; // Define bin edges
    let binned_data = bin_continuous(&data, &bins);
    println!("Binned Data: {:?}", binned_data);
}

In this implementation, we define a function that takes a slice of continuous data and an array of bin edges. For each value in the data, we determine which bin it falls into by checking against the bin edges. The resulting vector contains the indices of the bins for each input value, allowing us to categorize our continuous data effectively.

In conclusion, data transformation techniques such as scaling, encoding, and binning are pivotal in preparing datasets for machine learning applications. By understanding the necessity of these transformations and applying them using Rust, we can enhance the performance and interpretability of our models. Each technique serves its purpose, whether it be making features comparable in scale, converting categorical data into a usable format, or organizing continuous data into meaningful intervals. The practical implementations provided in this section serve as a foundation for further exploration and application of data transformation techniques in your machine learning projects using Rust.

18.4. Feature Engineering and Selection link

Feature engineering is a critical step in the machine learning pipeline that often determines the success of a predictive model. It involves the transformation of raw data into features that better capture the underlying patterns of the problem being solved. The transformation process is designed to enhance both model performance and interpretability by providing the machine learning algorithms with inputs that more directly represent the problem space. Raw data, in its original form, is frequently noisy, unstructured, or unsuitable for direct use in machine learning models. As a result, effective feature engineering is vital for improving model accuracy, reducing noise, and enabling models to generalize better to unseen data.

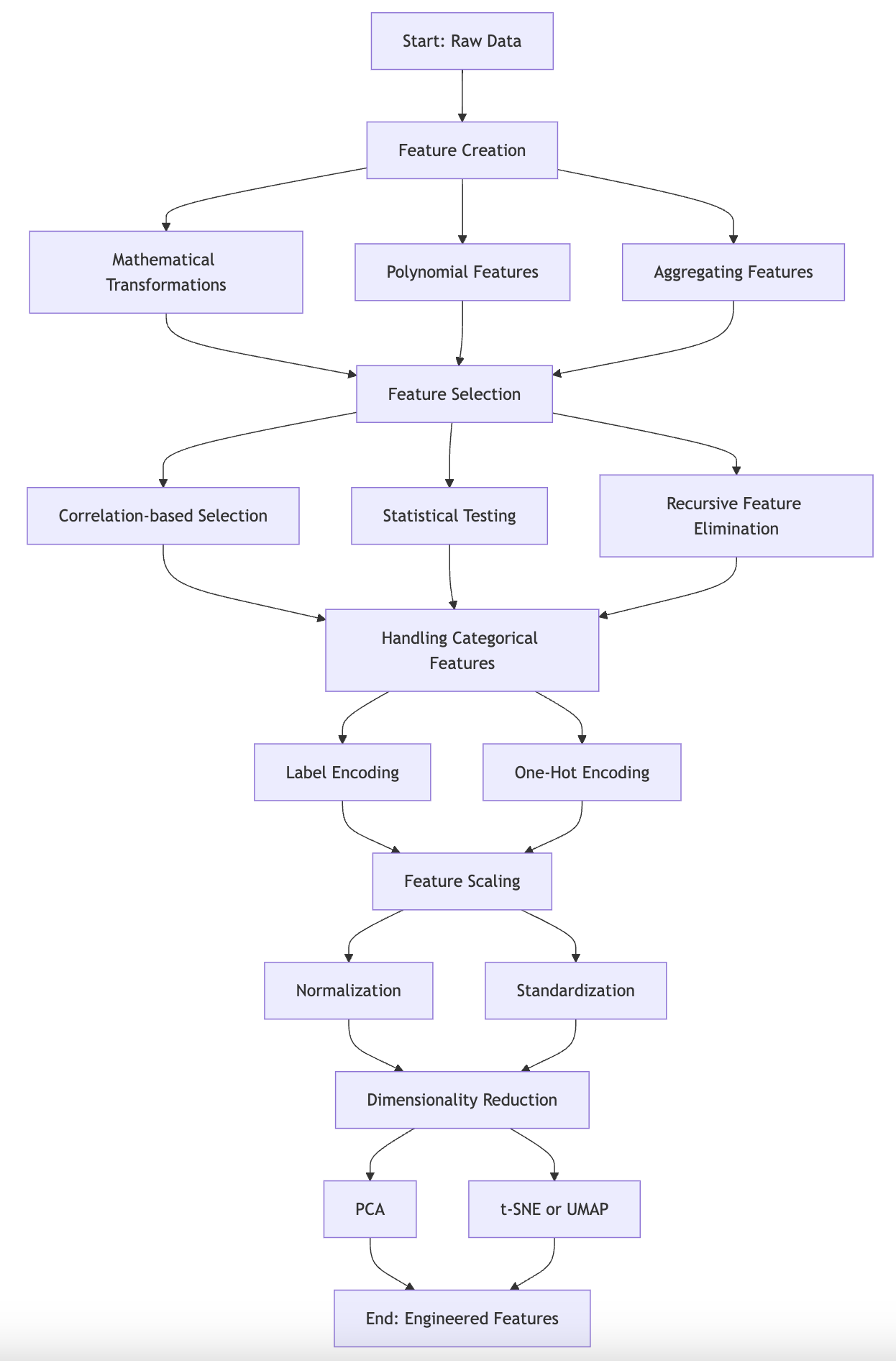
Figure 5: Illustration of features engineering.

The significance of feature engineering lies in its direct impact on the ability of machine learning models to discover meaningful patterns within the data. The process can be viewed as crafting representations of the data that make the relationships between inputs and outputs more apparent to the model. A well-engineered feature set can lead to dramatic improvements in predictive accuracy, whereas poorly chosen or uninformative features may introduce unnecessary noise, leading to overfitting or underfitting. Thus, the task of creating and selecting features is essential, as it lays the groundwork for the entire modeling process.

At the heart of feature engineering is the principle of feature selection, which involves identifying the most relevant and informative features for model training. Formally, let $\mathbf{X} \in \mathbb{R}^{n \times d}$ represent the feature matrix, where nnn is the number of samples and ddd is the number of features. The goal of feature selection is to choose a subset of features $S \subseteq \{1, 2, \dots, d\}$ such that the selected features $\mathbf{X}_S$ optimize model performance. Feature selection serves multiple purposes: it reduces the dimensionality of the dataset, which leads to faster training and prediction times, and it mitigates the risk of overfitting by eliminating irrelevant or redundant features. By focusing on the most informative features, models can generalize better to unseen data, improving their ability to make accurate predictions.

There are several approaches to feature selection, each offering different trade-offs in terms of computational efficiency and effectiveness. Broadly, feature selection methods are categorized into filter methods, wrapper methods, and embedded methods.

Filter methods assess the relevance of each feature based on its intrinsic properties, independent of the learning algorithm. A common mathematical approach in filter methods involves calculating the correlation coefficient between each feature $X_j$ and the target variable $Y$, where $Y \in \mathbb{R}^{n}$ represents the target values. Features with a high correlation (positive or negative) to the target are considered more informative. This can be formalized as maximizing the mutual information $I(X_j; Y)$, where mutual information measures the reduction in uncertainty about $Y$ given knowledge of $X_j$. Filter methods are computationally efficient, but they may fail to account for interactions between features.

Wrapper methods evaluate feature subsets by training the model on different combinations of features and selecting the subset that yields the best performance. Suppose the model's performance is measured by a loss function $\mathcal{L}(\mathbf{X}_S, Y)$ for a feature subset $S$. Wrapper methods involve solving the optimization problem:

$$\min_{S \subseteq \{1, 2, \dots, d\}} \mathcal{L}(\mathbf{X}_S, Y)$$

While wrapper methods are often more effective than filter methods because they account for interactions between features, they can be computationally expensive, especially for large feature sets, as they require repeatedly training the model.

Embedded methods integrate the feature selection process into the model training itself. A prominent example is LASSO (Least Absolute Shrinkage and Selection Operator), which adds an L1-regularization term to the objective function of the learning algorithm to induce sparsity in the feature weights. The regularized loss function for LASSO regression can be written as:

$$\mathcal{L}(\mathbf{X}, Y) + \lambda \sum_{j=1}^{d} |w_j|,$$

where $w_j$ is the weight of feature $X_j$ and $\lambda$ is a regularization parameter. The L1-norm penalty encourages many of the weights $w_j$ to become zero, effectively removing the corresponding features from the model. Embedded methods strike a balance between the efficiency of filter methods and the effectiveness of wrapper methods, as they incorporate feature selection directly into the training process.

Beyond feature selection, feature creation is another vital aspect of feature engineering. One common technique in feature creation is the generation of interaction terms, where new features are formed by multiplying two or more original features together. The purpose of interaction terms is to capture the combined effect of these features on the target variable. For example, if two features $x_1$ and $x_2$ are thought to have a joint influence on the target variable, their interaction term would be represented as $x_1 \times x_2$. This interaction term introduces a new dimension to the model, allowing it to capture more complex relationships between the input variables and the output.

Another powerful feature creation method is the generation of polynomial features. Polynomial features are created by raising original features to higher powers, which allows models to capture non-linear relationships between the features and the target variable. For example, a second-degree polynomial feature for a feature $x$ is $x^2$, and a third-degree polynomial feature is $x^3$. These transformations are especially useful in models that assume linear relationships, such as linear regression, as they enable the model to fit more complex patterns in the data.

Mathematically, if $\mathbf{X} \in \mathbb{R}^{n \times d}$ is the original feature matrix, the polynomial expansion of degree $k$ transforms each feature $X_j$ into new features $X_j^1, X_j^2, \dots, X_j^k$, creating a new feature space $\mathbf{X}' \in \mathbb{R}^{n \times kd}$. The expanded feature space can then be used to fit models that capture higher-order interactions and non-linearities in the data.

In practice, the application of feature engineering techniques in Rust can be efficiently implemented using libraries such as ndarray for numerical operations, combined with other specialized crates for data manipulation and model training. For example, interaction terms and polynomial features can be created by iterating over the feature matrix and applying element-wise transformations to generate the desired feature combinations. Rust’s concurrency features and memory management capabilities make it well-suited for handling large datasets and performing feature engineering at scale.

In summary, feature engineering is a crucial process that shapes the success of machine learning models by transforming raw data into meaningful representations. Through techniques such as interaction terms, polynomial features, and feature selection, machine learning practitioners can create features that capture the complexity of the underlying problem while also reducing noise and improving model interpretability. By implementing these techniques efficiently in Rust, practitioners can build scalable and high-performance machine learning pipelines that produce robust, accurate models.

To implement these feature engineering techniques in Rust, we can leverage its powerful data manipulation capabilities along with crates such as ndarray for numerical operations and linfa for machine learning tasks. Below is an example demonstrating how to create interaction terms and polynomial features in Rust, followed by a simple implementation of LASSO for feature selection.

First, let's assume we have a dataset represented as a two-dimensional array using the ndarray crate. We can start by constructing our interaction and polynomial features.

use ndarray::Array2;

fn create_interaction_terms(data: &Array2<f64>) -> Array2<f64> {
    let (rows, cols) = data.dim();
    let mut new_features = Array2::<f64>::zeros((rows, cols * (cols - 1) / 2));
    let mut idx = 0;

    for i in 0..cols {
        for j in i + 1..cols {
            let col_i = data.column(i).to_owned();
            let col_j = data.column(j).to_owned();
            new_features.column_mut(idx).assign(&(col_i * col_j));
            idx += 1;
        }
    }

    new_features
}

fn create_polynomial_features(data: &Array2<f64>, degree: usize) -> Array2<f64> {
    let (rows, cols) = data.dim();
    let mut new_features = Array2::<f64>::zeros((rows, cols * degree));

    for i in 0..cols {
        for d in 1..=degree {
            new_features.column_mut(i * degree + d - 1).assign(&(data.column(i).mapv(|x| x.powi(d as i32))));
        }
    }

    new_features
}

fn main() {
    let data = Array2::<f64>::from_shape_vec((5, 3), vec![1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0, 13.0, 14.0, 15.0]).unwrap();
    
    let interaction_terms = create_interaction_terms(&data);
    println!("Interaction Terms: {:?}", interaction_terms);

    let polynomial_features = create_polynomial_features(&data, 2);
    println!("Polynomial Features: {:?}", polynomial_features);
}

In this code, we define two functions: create_interaction_terms and create_polynomial_features. The first function generates interaction terms by multiplying pairs of features, while the second function generates polynomial features up to a specified degree. The main function demonstrates how to use these functions with a sample dataset.

For feature selection, we can implement a simple version of LASSO regression in Rust using the ndarray crate for numerical operations. The following example demonstrates how to perform LASSO regression:

use ndarray::prelude::*;

fn normalize_features(features: &Array2<f64>) -> Array2<f64> {
    let mean = features.mean_axis(Axis(0)).unwrap();
    let std_dev = features.std_axis(Axis(0), 0.0);
    
    (features - &mean) / &std_dev
}

fn lasso_regression(
    features: &Array2<f64>,
    target: &Array1<f64>,
    alpha: f64,
    learning_rate: f64,
    num_iterations: usize,
) -> Array1<f64> {
    let (n_samples, n_features) = features.dim();
    let mut weights = Array1::<f64>::zeros(n_features);
    let mut bias = 0.0;

    for _ in 0..num_iterations {
        let prediction = features.dot(&weights) + bias;
        let error = &prediction - target;

        // Gradient calculation
        let grad_w = features.t().dot(&error) / n_samples as f64 + alpha * weights.mapv(|w| w.signum());
        let grad_b = error.sum() / n_samples as f64;

        // Update weights and bias
        weights = &weights - &(learning_rate * &grad_w);
        bias -= learning_rate * grad_b;

        // Check for NaN or Inf
        if weights.iter().any(|&w| w.is_nan() || w.is_infinite()) || bias.is_nan() || bias.is_infinite() {
            panic!("NaN or Inf detected in weights or bias.");
        }
    }

    weights
}

fn main() {
    // Example data
    let features = Array2::<f64>::from_shape_vec((100, 3), (0..300).map(|x| x as f64 / 10.0).collect()).unwrap();
    let true_weights = Array1::from(vec![1.0, -2.0, 3.0]);
    let target = features.dot(&true_weights) + Array1::from_shape_vec(100, (0..100).map(|x| (x as f64 % 2.0) - 0.5).collect()).unwrap();

    // Normalize features
    let normalized_features = normalize_features(&features);

    // Lasso regression parameters
    let alpha = 0.1;
    let learning_rate = 0.001; // Adjusted learning rate
    let num_iterations = 1000;

    // Perform Lasso regression
    let weights = lasso_regression(&normalized_features, &target, alpha, learning_rate, num_iterations);

    println!("Estimated weights: {:?}", weights);
}

In this example, we define a dataset and apply LASSO regression to select significant features. The LASSO model applies a penalty to the coefficients of the features, effectively pushing less important ones towards zero. This helps identify the most relevant features for our model.

In summary, feature engineering and selection are essential components of building effective machine learning models. By leveraging techniques such as interaction terms, polynomial features, and feature selection methods like LASSO, practitioners can significantly enhance model performance and interpretability. Rust, with its powerful libraries and performance efficiency, provides an excellent environment for implementing these techniques effectively.

18.5. Handling Imbalanced Data link

In the realm of machine learning, data quality and distribution play a fundamental role in determining the effectiveness of models. One of the most pressing challenges encountered by practitioners is the presence of imbalanced datasets, where the distribution of classes is highly skewed—one class significantly outnumbers the others. This imbalance can severely affect model performance, particularly in classification tasks, by biasing the model toward the majority class while neglecting the minority class. The ramifications of such bias are especially pronounced in real-world applications, such as fraud detection or medical diagnosis, where the minority class is often of greater interest. For instance, in a medical diagnosis model, an imbalanced dataset where healthy cases far outnumber disease cases could lead to a model that correctly identifies the healthy cases but consistently fails to recognize the minority class, which in this case represents patients with the disease. Such failures can result in critical misclassifications, including a high rate of false negatives, which are particularly detrimental in sensitive applications.

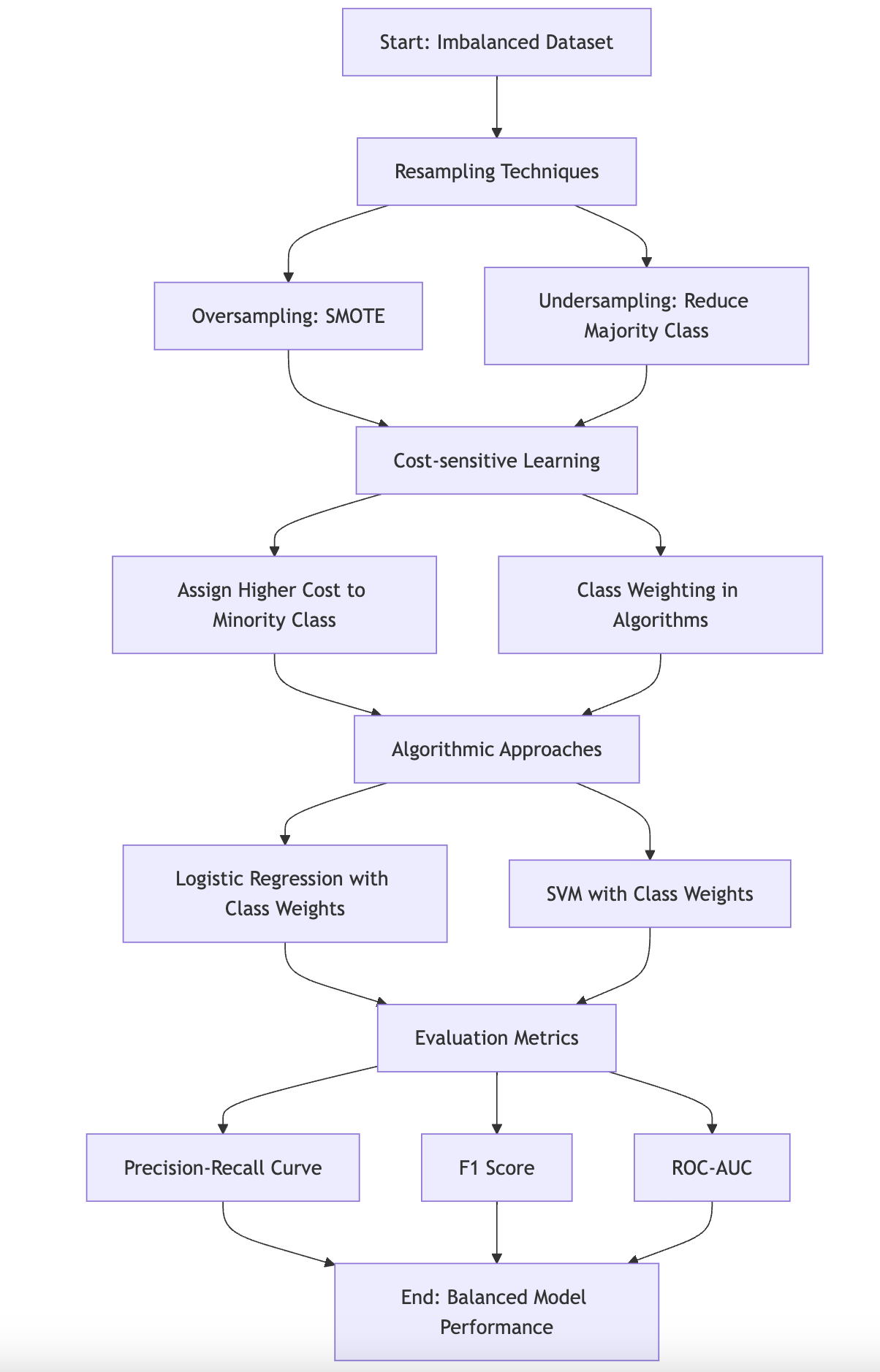
Figure 6: Illustration of handling imbalance data.

The mathematical consequences of imbalanced data stem from its effect on the decision boundary learned by classifiers. In the case of a binary classification problem, let the dataset $D$ consist of $n$ samples, each belonging to one of two classes: the majority class $C_1$ and the minority class $C_2$, with $|C_1| \gg |C_2|$. When training a classifier, the objective is typically to minimize a loss function, such as binary cross-entropy or mean squared error, over the dataset. However, in imbalanced datasets, the optimization process is dominated by the majority class $C_1$, as errors on the majority class contribute far more to the total loss than errors on the minority class. This skews the decision boundary toward the majority class, resulting in poor classification performance for the minority class.

To mitigate the effects of imbalanced datasets, several techniques have been developed. A common strategy is to apply resampling methods, which modify the class distribution in the training data to create a more balanced dataset. These methods can be broadly divided into oversampling and undersampling techniques.

Oversampling involves increasing the representation of the minority class by either duplicating existing samples or generating synthetic samples. One widely used technique for oversampling is the Synthetic Minority Over-sampling Technique (SMOTE), which generates synthetic samples by interpolating between existing minority class samples. Mathematically, for two samples $x_i$ and $x_j$ from the minority class $C_2$, SMOTE creates a new synthetic sample $x_{\text{new}}$ as follows:

$$ x_{\text{new}} = x_i + \lambda (x_j - x_i), $$

where $\lambda$ is a random value between 0 and 1. This technique introduces variability in the minority class by generating new, plausible samples that lie between existing points in the feature space. The advantage of oversampling is that it ensures the classifier is exposed to a sufficient number of minority class samples, allowing it to learn a more accurate decision boundary for both classes. However, oversampling can also increase the likelihood of overfitting, particularly if exact duplicates of the minority class are introduced.

Conversely, undersampling reduces the number of samples in the majority class to match the size of the minority class. This approach balances the dataset by randomly selecting a subset of the majority class $C_1$ such that $|C_1| \approx |C_2|$. While undersampling is computationally efficient and avoids overfitting to the minority class, it has the downside of discarding potentially valuable data from the majority class, which could lead to information loss and decreased model performance.

Beyond resampling techniques, another approach to handling imbalanced datasets is algorithm-level intervention, where the model is modified to account for the imbalance during the training process. One of the most effective interventions is cost-sensitive learning, which introduces a cost matrix to penalize the misclassification of minority class instances more heavily than majority class instances. Let $\mathcal{C}$ be a cost matrix, where $\mathcal{C}(i,j)$ represents the cost of classifying a sample from class $i$ as class $j$. In the case of binary classification, a simple cost matrix might assign a higher cost to false negatives (i.e., classifying a minority class sample as belonging to the majority class) than to false positives. The objective function, such as the loss function $\mathcal{L}(\theta)$ is modified to incorporate the cost matrix:

$$ L(yi,y^i),\mathcal{L}_{\text{cost-sensitive}}(\theta) = \sum_{i=1}^{n} \mathcal{C}(y_i, \hat{y}_i) \cdot \mathcal{L}(y_i, \hat{y}_i), $$

where $y_i$ is the true label, $\hat{y}_i$ is the predicted label, and $\mathcal{L}$ is the original loss function. By introducing different costs for different types of misclassifications, cost-sensitive learning encourages the model to focus more on the minority class, without necessarily modifying the dataset itself. This method is particularly useful when oversampling or undersampling is impractical, or when retaining the original data distribution is essential for the problem at hand.

In practice, the choice between resampling techniques and algorithmic interventions depends on the specific characteristics of the dataset and the problem being solved. Resampling methods are often used as a preprocessing step to balance the dataset before training, while cost-sensitive learning can be integrated directly into the model's learning process. These techniques can also be combined for more robust solutions to imbalanced data.

Implementing these methods in Rust can be achieved using libraries such as ndarray for numerical operations and linfa for machine learning tasks. For example, oversampling techniques like SMOTE can be implemented by identifying minority class samples, generating synthetic samples, and augmenting the dataset accordingly. Cost-sensitive learning can be incorporated by modifying the loss function to include a cost matrix, which adjusts the penalties for different types of errors.

In conclusion, imbalanced datasets present significant challenges in machine learning, often leading to models that perform poorly on the minority class. Techniques such as oversampling, undersampling, and cost-sensitive learning offer effective solutions for mitigating the impact of class imbalance. By balancing the dataset or adjusting the learning process to account for class imbalances, these methods improve the model's ability to generalize across all classes, leading to more robust and reliable predictions. In Rust, these techniques can be implemented efficiently, allowing for the development of high-performance machine learning models that handle imbalanced datasets with ease.

In Rust, implementing techniques to address imbalanced data can be achieved using various libraries and custom implementations. For example, the Synthetic Minority Over-sampling Technique (SMOTE) is a popular method used to create synthetic instances of the minority class. Below is a simple implementation of SMOTE in Rust, demonstrating how to generate synthetic samples based on existing minority class instances.

First, we need to set up our Rust project and add dependencies for numerical operations. We can use the ndarray crate for handling arrays and rand for random number generation. Here's how you would set up your Cargo.toml:

[dependencies]
ndarray = "0.16.1"
rand = "0.8.5"

Now, let’s implement a basic version of SMOTE:

use ndarray::{Array2, Array1};
use rand::Rng;

fn smote(data: &Array2<f64>, target: &Array1<f64>, minority_class: f64, k: usize, n_samples: usize) -> Array2<f64> {
    let mut rng = rand::thread_rng();
    let minority_indices: Vec<usize> = target.iter().enumerate()
        .filter(|&(_, &val)| val == minority_class)
        .map(|(index, _)| index)
        .collect();

    let mut synthetic_samples = Array2::zeros((n_samples, data.ncols()));

    for i in 0..n_samples {
        // Randomly select an instance from the minority class
        let rand_index = minority_indices[rng.gen_range(0..minority_indices.len())];
        let instance = data.row(rand_index).to_owned();

        // Generate synthetic sample by selecting a random neighbor
        let neighbor_index = minority_indices[rng.gen_range(0..minority_indices.len())];
        let neighbor = data.row(neighbor_index).to_owned();
        let diff = &neighbor - &instance;
        let gap = rng.gen::<f64>();
        let synthetic_sample = &instance + gap * &diff;

        synthetic_samples.row_mut(i).assign(&synthetic_sample);
    }

    synthetic_samples
}

fn main() {
    // Example dataset
    let data = Array2::from_shape_vec(
        (10, 3), // 10 samples, 3 features
        vec![
            1.0, 2.0, 1.5, // Class 0
            1.1, 2.1, 1.6,
            1.2, 2.2, 1.7,
            10.0, 10.0, 10.0, // Class 1 (minority)
            10.1, 10.1, 10.1,
            10.2, 10.2, 10.2,
            2.0, 3.0, 2.5, // Class 0
            2.1, 3.1, 2.6,
            2.2, 3.2, 2.7,
            10.3, 10.3, 10.3, // Class 1 (minority)
        ]
    ).unwrap();

    let target = Array1::from_vec(vec![
        0.0, 0.0, 0.0,  // Class 0
        1.0, 1.0, 1.0,  // Class 1 (minority)
        0.0, 0.0, 0.0,  // Class 0
        1.0,  // Class 1 (minority)
    ]);

    // Parameters for SMOTE
    let minority_class = 1.0; // Class to generate synthetic samples for
    let k = 1; // Number of nearest neighbors to consider (not used in this implementation)
    let n_samples = 5; // Number of synthetic samples to generate

    // Generate synthetic samples
    let synthetic_samples = smote(&data, &target, minority_class, k, n_samples);

    println!("Synthetic Samples:\n{:?}", synthetic_samples);
}

In this code, we first filter to find indices of the minority class. We then create synthetic samples by selecting random instances from the minority class and generating new instances by interpolating between them and their neighbors. The k parameter allows us to control the number of neighbors to consider for generating each synthetic sample, while n_samples indicates how many synthetic samples we wish to create.

Another practical approach to handling imbalanced data is the adjustment of class weights in algorithms. Many machine learning libraries in Rust, such as linfa, allow for the specification of class weights directly in the model training process. By providing higher weights for the minority class, the learning algorithm can be guided to pay more attention to it during training. Here’s an example of how you might apply class weighting using the linfa library:

use linfa::prelude::*;
use linfa_logistic::LogisticRegression;

let class_weights = vec![1.0, 10.0]; // Assume class 0 is the majority and class 1 is the minority
let model = LogisticRegression::fit(&dataset, Some(&class_weights)).unwrap();

In this code snippet, we define class weights, where the minority class (class 1) has a higher weight relative to the majority class (class 0). This simple adjustment can significantly influence the model's performance, encouraging it to focus on correctly classifying instances from the minority class.

In conclusion, handling imbalanced data is a multifaceted challenge that requires a combination of resampling techniques, algorithm adjustments, and thoughtful implementation in programming languages like Rust. By utilizing methods such as SMOTE and class weighting, practitioners can build more effective and fair machine learning models that are better equipped to handle the complexities of real-world data distributions. Employing these strategies ensures that models are not only accurate but also equitable in their predictions across different classes.

18.6 Dimensionality Reduction link

Dimensionality reduction is a crucial step in the data preprocessing and feature engineering pipeline of machine learning. Its primary purpose is to reduce the number of features in a dataset while retaining as much of the essential information as possible. High-dimensional datasets can often lead to issues such as overfitting, increased computational cost, and difficulties in visualizing the data. By applying dimensionality reduction techniques, we can mitigate these challenges, improve the efficiency of machine learning models, and enhance their interpretability.

At the core of dimensionality reduction lies the idea of transforming the original feature space into a new, lower-dimensional space. Various techniques have been developed for this purpose, among which Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), and t-Distributed Stochastic Neighbor Embedding (t-SNE) are some of the most prominent. Each of these methods operates under different assumptions and is suitable for different types of data and applications.

Principal Component Analysis (PCA) is one of the most widely used dimensionality reduction techniques. It works by identifying the directions (or principal components) along which the variance of the data is maximized. The fundamental idea is to project the original data onto a new set of orthogonal axes created from the eigenvectors of the covariance matrix of the data. By retaining only the top k eigenvectors corresponding to the largest eigenvalues, we can reduce the dimensionality of the dataset while preserving most of its variance. This method is particularly useful for datasets where the features are correlated, as PCA helps to unearth the underlying structure of the data.

Linear Discriminant Analysis (LDA), on the other hand, is a supervised dimensionality reduction technique. While PCA focuses on maximizing variance, LDA aims to maximize the separation between multiple classes in the dataset. By finding a set of linear combinations of the features that best separate the classes, LDA can effectively reduce dimensionality while preserving the discriminatory information. LDA is particularly useful in scenarios where the goal is to enhance classification performance.

t-Distributed Stochastic Neighbor Embedding (t-SNE) is a non-linear dimensionality reduction technique that excels in visualizing high-dimensional data in two or three dimensions. Unlike PCA and LDA, which are linear techniques, t-SNE focuses on preserving the local structure of the data. It converts similarities between data points into probabilities and attempts to minimize the divergence between the probability distributions of the high-dimensional and low-dimensional representations. This results in a meaningful visualization of clusters and patterns in the data, making t-SNE an invaluable tool for exploratory data analysis.

In summary, dimensionality reduction, which covered in other chapter of MLVR, is an essential technique in machine learning that helps to simplify datasets while retaining their essential characteristics. By employing methods like PCA, LDA, and t-SNE, practitioners can not only enhance the performance of their models but also gain valuable insights into the underlying structure of the data. Implementing these techniques in Rust allows developers to leverage the language's performance and safety features while tackling complex data science problems efficiently.

18.7. Data Augmentation link

Data augmentation is an essential technique in machine learning, particularly in fields such as computer vision and natural language processing (NLP), where the availability of large and diverse datasets is critical for building robust models. The fundamental principle behind data augmentation is the artificial expansion of the training dataset by applying various transformations to the existing data. These transformations generate new data points, allowing the model to learn from a broader range of input variations. By introducing more diversity into the training process, data augmentation helps mitigate overfitting, improves generalization to unseen data, and makes models more resilient to variations in real-world inputs.

Figure 7: Illustration of data augmentation in computer vision.

In the context of computer vision, data augmentation leverages transformations applied to images to create new, yet semantically equivalent, examples from the original dataset. Suppose we have an image $I \in \mathbb{R}^{h \times w \times 3}$ , where $h$ and $w$ denote the height and width of the image, and the third dimension corresponds to the color channels. The goal is to apply a transformation $T: \mathbb{R}^{h \times w \times 3} \to \mathbb{R}^{h' \times w' \times 3}$ that modifies the image while preserving its content. For example, rotation by an angle $\theta$ can be expressed as:

$$T_{\text{rotation}}(I) = R_\theta \cdot I,$$

where $R_\theta$ is the rotation matrix that rotates the image by $\theta$ degrees. Other transformations commonly used in computer vision include horizontal flips, scaling, cropping, and brightness or contrast adjustments. For example, horizontal flipping can be represented by a transformation that reflects the image along the vertical axis:

$$T_{\text{flip}}(I) = I_{\text{flipped}}.$$

These transformations generate multiple versions of the same image, enabling the model to learn from different orientations, scales, and lighting conditions. This is particularly useful in cases where datasets are small or imbalanced. For example, in a facial recognition system, augmenting an image by rotating it slightly or flipping it horizontally allows the model to learn facial features that are invariant to changes in orientation or position.

Another common data augmentation technique in computer vision is color jittering, where the color properties of the image, such as brightness, contrast, saturation, and hue, are randomly modified. This transformation can be described mathematically by adjusting the pixel values in each color channel:

$$T_{\text{color}}(I) = \alpha I + \beta,$$

where $\alpha$ controls the contrast and $\beta$ modifies the brightness of the image. By applying these transformations, the model becomes more robust to changes in lighting conditions, which is crucial for real-world applications where lighting can vary significantly.

In natural language processing (NLP), data augmentation involves transforming text data to generate syntactically or semantically varied versions of the original text. One of the simplest approaches is synonym replacement, where specific words in the text are replaced by their synonyms. Consider a sentence $S = [w_1, w_2, \dots, w_n]$, where wiw_iwi is a word in the sentence. A synonym replacement transformation replaces a word $w_i$ with one of its synonyms $w_i$, drawn from a predefined set of synonyms $\mathcal{S}(w_i)$. The augmented sentence $S'$ is then:

$$ S' = [w_1, \dots, w_i', \dots, w_n], \quad \text{where} \, w_i' \in \mathcal{S}(w_i). $$

This transformation preserves the overall meaning of the sentence while introducing lexical diversity. For example, replacing "happy" with "joyful" or "content" allows the model to learn that these words convey similar meanings in different contexts. Other techniques include random insertion, where random words from a vocabulary are inserted into the text, and random deletion, where certain words are removed to create a slightly shorter version of the original sentence.

More advanced augmentation techniques in NLP include back-translation, where a sentence is translated from the source language into another language and then back to the original language. Let $S$ be a sentence in the source language $L_1$, and let $\mathcal{T}_{L_1 \to L_2}(S)$ represent the translation of the sentence into a target language $L_2$. Back-translation creates an augmented sentence S′S'S′ by translating back to $L_1$:

$$S' = \mathcal{T}_{L_2 \to L_1}(\mathcal{T}_{L_1 \to L_2}(S)).$$

Back-translation allows the model to encounter variations in phrasing while retaining the original meaning, which improves its ability to generalize across different linguistic expressions. For instance, translating "The cat is on the mat" into French and back to English might result in "The mat is under the cat," exposing the model to different syntactic structures.

From a mathematical perspective, data augmentation can be viewed as a transformation $T$ applied to the original dataset $\mathcal{D}$, yielding an augmented dataset $\mathcal{D}'$ :

$$\mathcal{D}' = \{T(x) \mid x \in \mathcal{D}\}.$$

The goal is to apply transformations $T$ that preserve the essential characteristics of the data while expanding the dataset to include more variability. By augmenting the dataset, the model is exposed to a wider range of examples, which helps prevent overfitting to the training data and enhances the model's ability to generalize to unseen examples.

Implementing these data augmentation techniques in Rust can be achieved using libraries such as image for manipulating images and nlp crates for handling text data. For example, image rotation can be implemented by applying rotation matrices to pixel coordinates, while synonym replacement in NLP can be achieved by utilizing dictionaries or pre-trained word embeddings to identify and replace synonyms.

In conclusion, data augmentation is a vital tool in machine learning, particularly in domains where data collection is costly or limited. Through transformations such as rotations, flips, scaling, and synonym replacement, data augmentation artificially increases the size and diversity of the training dataset, thereby improving model performance and generalization. These techniques help mitigate overfitting by introducing new variations of the data, allowing models to learn more robust representations that are less sensitive to specific patterns or noise present in the training set. In Rust, data augmentation can be efficiently implemented, providing practitioners with the tools needed to build resilient and high-performance models in both computer vision and natural language processing tasks.

To implement data augmentation in Rust, we can leverage the capabilities of libraries such as image for image processing and regex for text manipulation. Below is an example of how to perform image augmentation through simple transformations. First, we will need to add the image crate to our Cargo.toml file:

[dependencies]
image = "0.25.2"

Next, we can create a Rust function to perform basic image augmentations such as rotation and flipping. The following code demonstrates how to read an image, apply transformations, and save the augmented images:

use image;

fn augment_image(image_path: &str) {
    let img = image::open(image_path).expect("Failed to open image");
    
    // Rotate the image by 90 degrees
    let rotated_img = img.rotate90();
    rotated_img.save("augmented_rotated.png").expect("Failed to save rotated image");
    
    // Flip the image horizontally
    let flipped_img = img.fliph();
    flipped_img.save("augmented_flipped.png").expect("Failed to save flipped image");
    
    // Additional transformations can be added here
}

fn main() {
    augment_image("path/to/your/image.png");
}

In this example, we read an image from a specified path, apply a 90-degree rotation, and flip the image horizontally. The augmented images are then saved as new files, allowing the model to train on these transformed versions. This approach can be expanded further by incorporating additional augmentation techniques, such as scaling, cropping, and color jittering.

For text augmentation, we can use the regex crate to implement simple techniques like synonym replacement. To do so, we first need to add regex to our Cargo.toml:

[dependencies]
regex = "1.11.0"

Next, we can create a function that replaces certain words with their synonyms. Although a more comprehensive synonym dictionary would be ideal, for this example, we will create a simple mapping:

use regex::Regex;
use std::collections::HashMap;

fn augment_text(text: &str) -> String {
    let synonyms: HashMap<&str, &str> = [
        ("happy", "joyful"),
        ("fast", "quick"),
        ("sad", "unhappy"),
    ]
    .iter()
    .cloned()
    .collect();

    let mut augmented_text = text.to_string();
    
    for (word, synonym) in &synonyms {
        let re = Regex::new(&format!(r"\b{}\b", word)).unwrap();
        augmented_text = re.replace_all(&augmented_text, *synonym).to_string();
    }

    augmented_text
}

fn main() {
    let original_text = "I am happy and fast.";
    let augmented_text = augment_text(original_text);
    println!("Original: {}", original_text);
    println!("Augmented: {}", augmented_text);
}

In this code, we define a simple synonym mapping and use a regular expression to replace occurrences of specified words with their synonyms. The output demonstrates how we can create variations of the original text, which can be useful for training NLP models.

Evaluating the impact of data augmentation on model performance is crucial. After applying these techniques, it is essential to train your model on both the original and augmented datasets. Monitoring metrics such as accuracy, precision, and recall can help assess improvements in generalization and robustness. By systematically comparing the performance of models trained on augmented versus non-augmented data, we can gain insights into the effectiveness of the chosen augmentation strategies.

In summary, data augmentation is a powerful technique that can significantly enhance the performance of machine learning models, particularly in scenarios with limited training data. By utilizing Rust's capabilities, we can efficiently implement various augmentation methods for both image and text datasets, ultimately improving model robustness and generalization. Whether through simple transformations or more complex techniques, the strategic use of data augmentation can lead to more resilient and effective models in real-world applications.

18.8. Conclusion link

Chapter 18 equips you with essential skills in Data Processing and Feature Engineering, enabling you to prepare and transform data effectively for machine learning tasks. By mastering these techniques in Rust, you will enhance the quality and performance of your models, laying a strong foundation for successful machine learning projects.

18.8.1. Further Learning with GenAI link

By exploring these questions, you will deepen your knowledge of the theoretical foundations, practical applications, and advanced techniques in data preparation, equipping you to build robust and high-performing machine learning models.

• Explain the importance of data processing in the machine learning pipeline. How does proper data processing impact model performance, and what are the key steps involved in preparing data for analysis? Implement a basic data processing pipeline in Rust.

• Discuss the role of data cleaning in improving data quality. What are the common issues encountered during data cleaning, and how can they be addressed effectively? Implement data cleaning techniques in Rust and apply them to a noisy dataset.

• Analyze the impact of missing data on model performance. How do different strategies for handling missing values, such as imputation or deletion, affect the accuracy and robustness of machine learning models? Implement missing data handling techniques in Rust and evaluate their impact on a dataset.

• Explore the concept of data normalization and standardization. Why is scaling important for certain machine learning algorithms, and how do normalization and standardization differ in their effects on data? Implement scaling techniques in Rust and apply them to a dataset with varying feature magnitudes.

• Discuss the challenges of encoding categorical variables in machine learning. What are the pros and cons of different encoding methods, such as one-hot encoding, label encoding, and target encoding? Implement various encoding techniques in Rust and compare their impact on model performance.

• Analyze the role of outlier detection in data preprocessing. How do outliers affect machine learning models, and what methods can be used to identify and handle them? Implement outlier detection techniques in Rust, such as Z-score and IQR, and apply them to a dataset with extreme values.

• Explore the importance of feature engineering in model performance. How does creating new features, such as interaction terms or polynomial features, enhance the predictive power of machine learning models? Implement feature engineering techniques in Rust and apply them to a regression task.

• Discuss the concept of feature selection in the context of high-dimensional data. What are the benefits of reducing the feature space, and what techniques can be used to select the most relevant features? Implement feature selection methods in Rust, such as Recursive Feature Elimination (RFE) or LASSO, and apply them to a complex dataset.

• Analyze the challenges of handling imbalanced data in machine learning. How do class imbalances affect model performance, and what strategies can be used to address this issue? Implement techniques for handling imbalanced data in Rust, such as SMOTE or adjusting class weights, and evaluate their effectiveness.

• Explore the use of dimensionality reduction techniques in data processing. How do methods like PCA, LDA, and t-SNE help in reducing the feature space while preserving important information? Implement dimensionality reduction techniques in Rust and apply them to a high-dimensional dataset.

• Discuss the concept of data augmentation in machine learning. How does augmenting data improve model generalization, particularly in fields like computer vision and NLP? Implement data augmentation techniques in Rust and apply them to an image or text dataset.

• Analyze the impact of feature scaling on model convergence. How does scaling affect the convergence speed of gradient-based algorithms, such as linear regression or neural networks? Implement feature scaling in Rust and evaluate its impact on model training time and accuracy.

• Explore the use of cross-validation in data preprocessing. How does cross-validation help in assessing the effectiveness of data preprocessing steps, such as feature selection or data transformation? Implement cross-validation in Rust and apply it to evaluate different preprocessing strategies.

• Discuss the challenges of working with categorical and numerical features together. How can feature engineering techniques be applied differently to categorical and numerical features to optimize model performance? Implement a mixed-feature preprocessing pipeline in Rust and apply it to a dataset with both types of features.

• Analyze the role of interaction terms in feature engineering. How do interaction terms capture complex relationships between features, and what are the best practices for generating and selecting these terms? Implement interaction terms in Rust and evaluate their impact on a predictive model.

• Explore the importance of feature extraction in domains like NLP and computer vision. How do techniques like TF-IDF, word embeddings, or image filters enhance the quality of features in these fields? Implement feature extraction methods in Rust and apply them to a text or image dataset.

• Discuss the concept of automated feature engineering. How can automation tools, such as FeatureTools or AutoML, assist in generating and selecting features, and what are the trade-offs compared to manual feature engineering? Implement automated feature engineering in Rust and compare its results with manual techniques.

• Analyze the impact of noise reduction on model performance. How do techniques like filtering, smoothing, or denoising improve the quality of data, and when should they be applied? Implement noise reduction methods in Rust and apply them to a dataset with high variability.

• Explore the use of feature importance scores in model interpretation. How do models like decision trees or ensemble methods provide insights into feature importance, and how can these insights be used to refine feature engineering? Implement feature importance analysis in Rust and use it to guide feature selection in a machine learning model.

Each prompt encourages you to think critically about the data preprocessing steps and to apply your knowledge to create more accurate and interpretable models.

18.8.2. Hands On Practices link

These exercises are designed to be challenging and in-depth, requiring you to apply both theoretical knowledge and practical skills in Rust.