20.1. Introduction to Large-Scale Machine Learning link

Large-scale machine learning refers to the application of machine learning techniques to vast amounts of data, often exceeding the capacities of traditional computational frameworks. In today’s data-driven world, the sheer volume of data generated necessitates sophisticated methods to extract meaningful insights and predictions. The importance of large-scale machine learning lies not only in its ability to process big data but also in its potential to uncover patterns and trends that would be imperceptible with smaller datasets. This chapter delves into the fundamental and conceptual ideas surrounding large-scale machine learning, alongside practical implementations using Rust, a language known for its performance and safety.

Figure 1: Complexity of large scale ML model deployment.

The challenges posed by large-scale machine learning are multifaceted. One of the primary concerns is computational complexity, which increases significantly as the size of the dataset grows. Algorithms that were once feasible with smaller datasets may become impractical due to the time required for training and inference. This necessitates the development of more efficient algorithms and optimization techniques that can handle the increased workload without compromising performance. Moreover, memory constraints are a critical issue, as traditional data storage options may not be sufficient to accommodate the vast amounts of data typically involved in large-scale machine learning tasks. As a result, strategies such as data streaming and mini-batching become vital to ensure that the system can handle data efficiently without overwhelming the available memory.

Another significant challenge is data distribution. Data is often not stored in a single location, leading to the need for distributed computing frameworks that can process data across multiple machines or nodes. This introduces additional complexity in terms of data synchronization, load balancing, and fault tolerance. Rust's unique features, such as its ownership system, concurrent programming capabilities, and low-level memory management, make it an excellent choice for tackling these challenges. By leveraging Rust's strengths, developers can create robust applications that perform well even with large datasets.

To illustrate the practical application of large-scale machine learning in Rust, consider a simple example where we need to handle a large dataset for a linear regression task. In this scenario, we will utilize Rust's memory management capabilities to load data efficiently and perform computations using parallel processing to speed up the training process.

First, we can use the csv crate to read a large CSV file containing our dataset. Rust's ownership model ensures that we manage memory efficiently, so we can avoid common pitfalls such as memory leaks or buffer overflows. Here is a snippet demonstrating how to read a large dataset:

use csv::ReaderBuilder;
use std::error::Error;

fn read_large_dataset(file_path: &str) -> Result<Vec<(f64, f64)>, Box<dyn Error>> {
    let mut reader = ReaderBuilder::new().has_headers(true).from_path(file_path)?;
    let mut data = Vec::new();

    for result in reader.records() {
        let record = result?;
        let x: f64 = record[0].parse()?;
        let y: f64 = record[1].parse()?;
        data.push((x, y));
    }

    Ok(data)
}

In this code, we define a function read_large_dataset that reads a CSV file and returns a vector of tuples containing the data points. By utilizing iterators and the ? operator, Rust allows us to handle errors gracefully while ensuring efficient memory usage.

Next, to implement the linear regression model, we can leverage parallel processing to speed up computations. Rust's rayon crate provides an easy way to perform parallel iterations. Below is an example of how we can calculate the coefficients of a simple linear regression model:

use rayon::prelude::*;

fn linear_regression(data: &Vec<(f64, f64)>) -> (f64, f64) {
    let n = data.len() as f64;

    let (sum_x, sum_y, sum_xy, sum_x2): (f64, f64, f64, f64) = data
        .par_iter()
        .map(|&(x, y)| (x, y, x * y, x * x))
        .reduce(
            || (0.0, 0.0, 0.0, 0.0),
            |(s1, s2, s3, s4), (x, y, xy, x2)| (s1 + x, s2 + y, s3 + xy, s4 + x2),
        );

    let slope = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x.powi(2));
    let intercept = (sum_y - slope * sum_x) / n;

    (intercept, slope)
}

In this linear_regression function, we utilize the par_iter method to perform computations concurrently. This allows us to calculate the sums needed to derive the slope and intercept of the linear regression model efficiently. The use of Rust's type system ensures that we maintain safety while optimizing performance.

In conclusion, large-scale machine learning presents significant challenges, from computational complexity and memory constraints to data distribution issues. However, Rust's powerful features offer a robust framework for addressing these challenges. By utilizing Rust’s memory management capabilities and parallel processing, developers can implement efficient solutions for handling large datasets, enabling them to harness the full potential of machine learning in a data-rich environment. As we continue to explore large-scale machine learning in Rust, we will delve into more advanced techniques and frameworks that can further enhance our ability to work with big data.

20.2. Data Parallelism and Distributed Computing link

In the realm of large-scale machine learning, the ability to efficiently process vast amounts of data and model complexity is paramount. Data parallelism and distributed computing serve as foundational strategies that enable the scaling of machine learning algorithms to handle large datasets and train complex models. At its core, data parallelism involves breaking down a dataset into smaller subsets that can be processed simultaneously across multiple processors or nodes. This approach not only accelerates the training process but also allows for the utilization of available computational resources more effectively.

Figure 2: Complexity map of data parallelism and distributed computing.

Distributed computing extends this concept by enabling the execution of processes across multiple machines, often forming a cluster that collaborates to tackle large-scale tasks. In the context of machine learning, this means that both data and model training can be distributed, allowing various components of the algorithm to run concurrently. One of the key strategies in this framework is data partitioning, which involves dividing the dataset into manageable chunks that can be processed independently. This partitioning is crucial as it minimizes the amount of data that needs to be communicated between nodes, thereby reducing communication overhead and enhancing overall efficiency.

When implementing data parallelism in Rust, one can leverage powerful libraries such as Rayon, which provides an easy and efficient way to parallelize data processing tasks. With Rayon, developers can utilize Rust’s inherent safety features while simultaneously benefiting from concurrency, allowing for seamless integration of parallel computing into machine learning workflows. For instance, consider a scenario where we need to compute a simple transformation on a dataset stored in a vector. Using Rayon, we can transform the data in parallel, significantly reducing the time required for computation:

use rayon::prelude::*;

fn main() {
    let data: Vec<i32> = (1..=10_000).collect();
    let transformed: Vec<i32> = data.par_iter()
                                    .map(|&x| x * 2)
                                    .collect();

    println!("{:?}", &transformed[0..10]); // Display the first 10 results
}

In this example, the par_iter() method allows for parallel iteration over the vector, and the transformation is applied to each element concurrently. This is a simple illustration; however, in the context of machine learning, such transformations can represent preprocessing steps that need to be applied to large datasets before training a model.

The trade-offs between parallelism and communication overhead must also be carefully considered. While parallel processing can lead to significant speedups, it often introduces the challenge of synchronizing data across threads or nodes. Excessive communication between distributed nodes can lead to bottlenecks that negate the benefits of parallelism. Therefore, careful design is required to balance the workload and minimize the communication costs. For example, when training a machine learning model across multiple nodes, each node can be assigned a portion of the dataset to train a local model. After a predefined number of iterations, the local models can be aggregated to form a global model. This approach is commonly known as federated learning.

In Rust, implementing a basic distributed training setup may involve using a messaging framework like tokio or actix. Here, we can create an architecture that splits the dataset across different nodes and allows them to communicate their updates back to a central node. Below is a simplified example demonstrating how one might set up such a system with tokio:

// Append Cargo.toml

[dependencies]
tokio = { version = "1.40.0", features = ["full"] }

use tokio::sync::mpsc;
use std::sync::{Arc, Mutex};

struct Model {
    weights: Vec<f32>,
}

async fn train_model(data: Vec<f32>, model: Arc<Mutex<Model>>, tx: mpsc::Sender<Vec<f32>>) {
    let mut local_weights = vec![0.0; data.len()]; // Initialize local weights
    // Simulate training process
    for &datum in &data {
        // Update local weights based on datum
        local_weights.push(datum * 0.1); // Dummy operation
    }
    // Send local weights back to the main node
    let _ = tx.send(local_weights).await;
}

#[tokio::main]
async fn main() {
    let (tx, mut rx) = mpsc::channel(32);
    let model = Arc::new(Mutex::new(Model { weights: vec![] }));

    // Simulate splitting dataset and training on different nodes
    let datasets = vec![vec![1.0, 2.0], vec![3.0, 4.0]];
    for data in datasets {
        let model_clone = Arc::clone(&model);
        let tx_clone = tx.clone();
        tokio::spawn(async move {
            train_model(data, model_clone, tx_clone).await;
        });
    }

    drop(tx);

    // Aggregate results from training
    while let Some(local_weights) = rx.recv().await {
        let mut model = model.lock().unwrap();
        model.weights.extend(local_weights); // Aggregate weights
    }

    println!("Final model weights: {:?}", model.lock().unwrap().weights);
}

In this example, we use the tokio asynchronous runtime to simulate multiple nodes training on different data partitions. Each node processes its subset of data and sends the local model weights back to a central node via a channel. Finally, the central node aggregates these weights, illustrating a basic form of distributed model training.

In summary, data parallelism and distributed computing are critical components of scaling machine learning algorithms. By understanding and implementing these concepts in Rust, developers can harness the power of parallel processing and distributed systems to tackle large datasets and complex models. The careful design of data partitioning and communication strategies will ultimately dictate the efficiency and scalability of machine learning applications in a distributed environment.

20.3. Stochastic Gradient Descent (SGD) and Its Variants link

Stochastic Gradient Descent (SGD) is a fundamental optimization algorithm widely used in the field of machine learning, particularly for training neural networks and other models on large-scale datasets. Unlike traditional gradient descent, which computes the gradient of the loss function using the entire dataset, SGD updates the model parameters using a single data point or a small batch of data at each iteration. This characteristic makes SGD particularly well-suited for large-scale learning, as it allows for more frequent updates and can lead to faster convergence. The algorithm's efficiency and effectiveness are further enhanced by its variants, such as Mini-batch SGD and Asynchronous SGD, which introduce additional flexibility and speed in training.

The core idea of SGD is to approximate the gradient of the loss function with a subset of data rather than the entire dataset. By doing so, the algorithm can take advantage of the stochastic nature of the data, which not only helps in avoiding local minima but also significantly reduces the computational burden. The convergence of SGD is generally faster than traditional gradient descent, especially when dealing with large datasets. This speed is achieved by updating the model parameters more frequently, which helps the optimization process escape saddle points and navigate the loss landscape efficiently.

An important consideration when implementing SGD is the choice of batch size and learning rate. The batch size determines how many samples are used to compute each update, while the learning rate controls the size of the steps taken toward the minimum of the loss function. For large-scale datasets, mini-batch SGD is often preferred, as it strikes a balance between the efficiency of SGD and the stability of traditional gradient descent. In mini-batch SGD, the dataset is divided into small batches, and the model parameters are updated after each batch is processed. This approach not only allows for faster convergence but also helps in reducing the variance of the updates, leading to more consistent training performance.

Now, let's delve into the practical implementation of SGD and its variants in Rust. To demonstrate this, we will implement a simple version of SGD and mini-batch SGD for a linear regression task. We will start by defining a struct for our linear regression model and the necessary methods to perform the training using SGD.

use rand::seq::SliceRandom;

#[derive(Debug)]
struct LinearRegression {
    weights: Vec<f64>,
    learning_rate: f64,
}

impl LinearRegression {
    fn new(features: usize, learning_rate: f64) -> Self {
        let weights = vec![0.0; features];
        LinearRegression { weights, learning_rate }
    }

    fn predict(&self, input: &Vec<f64>) -> f64 {
        self.weights.iter().zip(input.iter()).map(|(w, x)| w * x).sum()
    }

    fn update_weights(&mut self, input: &Vec<f64>, error: f64) {
        for (w, x) in self.weights.iter_mut().zip(input.iter()) {
            *w -= self.learning_rate * error * x;
        }
    }

    fn train(&mut self, data: &Vec<(Vec<f64>, f64)>, epochs: usize) {
        let mut rng = rand::thread_rng();
        for _ in 0..epochs {
            let mut shuffled_data = data.clone();
            shuffled_data.shuffle(&mut rng);
            for (input, target) in shuffled_data.iter() {
                let prediction = self.predict(input);
                let error = target - prediction;
                self.update_weights(input, error);
            }
        }
    }
}

In this code, we define a LinearRegression struct that holds the weights and the learning rate. The predict method calculates the predicted value based on the input features, while the update_weights method adjusts the weights according to the calculated error. The train method implements the core of the SGD algorithm, where it shuffles the dataset and iterates through each data point to update weights.

Next, we can implement mini-batch SGD, which processes a small batch of samples at each iteration rather than a single sample. This adjustment will allow us to see the performance improvements when training on larger datasets.

impl LinearRegression {
    fn train_mini_batch(&mut self, data: &Vec<(Vec<f64>, f64)>, epochs: usize, batch_size: usize) {
        let mut rng = rand::thread_rng();
        for _ in 0..epochs {
            let mut shuffled_data = data.clone();
            shuffled_data.shuffle(&mut rng);
            for batch in shuffled_data.chunks(batch_size) {
                let mut batch_errors = vec![0.0; batch.len()];
                for (i, (input, target)) in batch.iter().enumerate() {
                    let prediction = self.predict(input);
                    batch_errors[i] = target - prediction;
                }
                for (i, (input, _)) in batch.iter().enumerate() {
                    self.update_weights(input, batch_errors[i]);
                }
            }
        }
    }
}

In the train_mini_batch method, we shuffle the data and then process it in chunks of the specified batch size. For each batch, we compute the prediction errors and update the weights based on the accumulated errors from that batch. This method can significantly speed up the training process, particularly when working with large datasets.

To tune the hyperparameters effectively, such as the learning rate and batch size, one may employ techniques such as grid search or random search, potentially with cross-validation to evaluate model performance. In practice, it's crucial to monitor the loss function during training to ensure that the learning rate is not too high (causing divergence) or too low (leading to slow convergence).

In conclusion, Stochastic Gradient Descent and its variants, like Mini-batch SGD, are powerful tools for optimizing machine learning models on large datasets. The flexibility and efficiency of these methods make them indispensable in modern machine learning workflows, especially when implemented in a performant language like Rust. By understanding the underlying principles of SGD and its variants, as well as how to implement them in Rust, practitioners can effectively tackle the challenges posed by large-scale machine learning tasks.

20.4. Online Learning and Incremental Algorithms link

In the realm of machine learning, the ability to process data sequentially and adaptively is becoming increasingly important. This is particularly true in large-scale applications, where data is generated continuously, often at high velocities. Online learning and incremental algorithms stand out as robust approaches to this challenge, allowing models to learn from data streams without the need to retrain from scratch on the entire dataset. Online learning typically refers to the paradigm where data arrives in a sequential manner, enabling the model to update its parameters incrementally with each new observation. This is in contrast to traditional batch learning methods, which require access to the entire dataset before learning can commence.

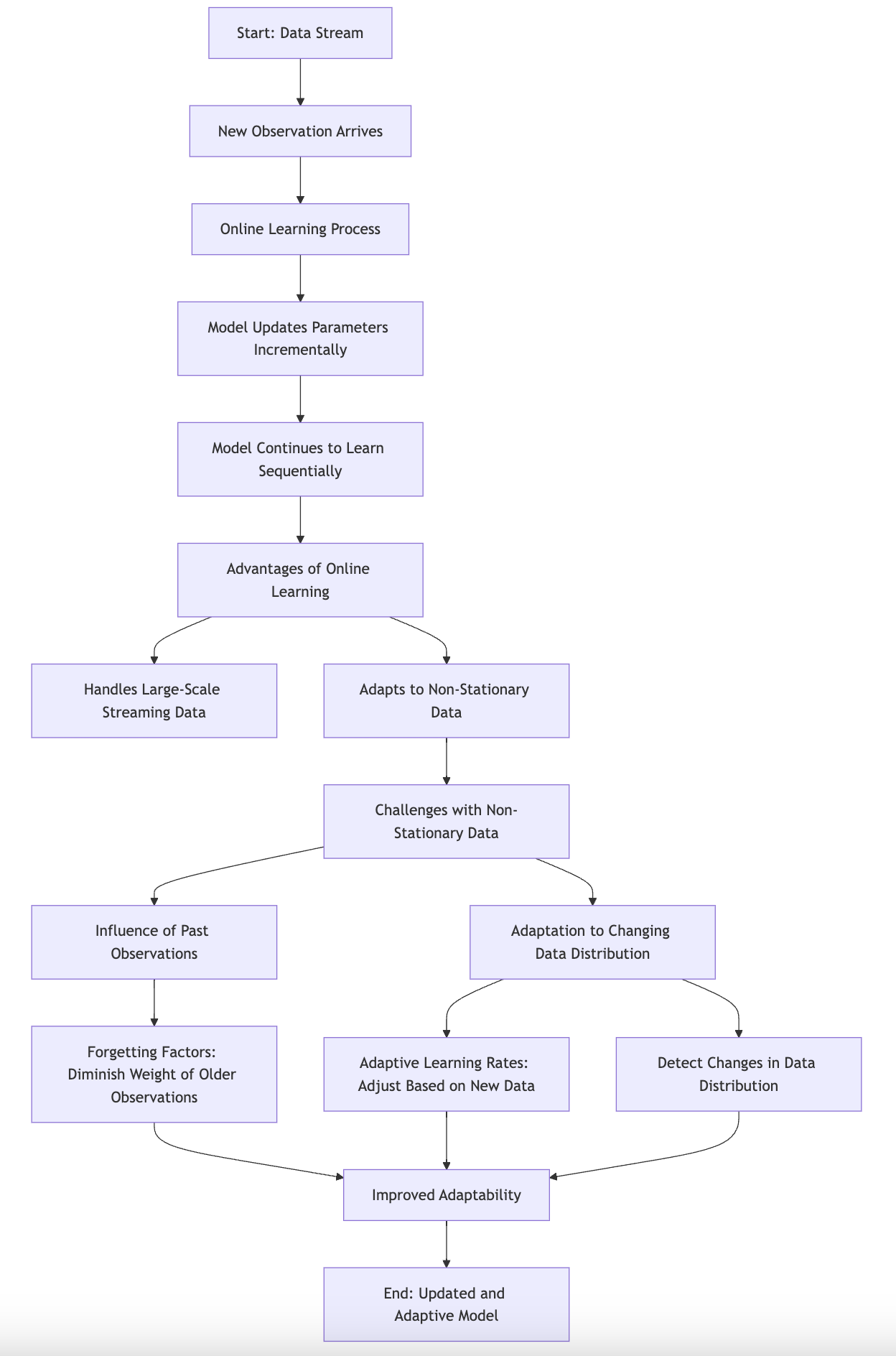
Figure 3: Illustration of Online Learning and Incremental Algorithms.

The fundamental ideas behind online learning emphasize its suitability for environments characterized by large-scale and streaming data. In online learning, the model continuously updates its parameters with each new data point it encounters, allowing it to adapt to changes in the underlying data distribution. This is particularly advantageous in scenarios where data is non-stationary, meaning that the statistical properties of the data may change over time. For example, in financial markets, stock prices fluctuate based on a myriad of factors, and models that can adapt to these changes are essential for making timely predictions.

However, while online learning offers many benefits, it also presents challenges, particularly when dealing with non-stationary data. The key difficulty lies in determining how much influence past observations should have on the current model. As new data arrives, older data may become less relevant, necessitating strategies for model adaptation. Techniques such as forgetting factors, which diminish the weight of older observations, or the use of adaptive learning rates can help address these challenges. Additionally, incorporating mechanisms for detecting changes in the data distribution can further enhance the adaptability of online learning models.

To illustrate the practical implementation of online learning in Rust, we can consider two fundamental algorithms: Stochastic Gradient Descent (SGD) and the Perceptron. Both of these algorithms are well-suited for online learning scenarios due to their ability to update model parameters incrementally. Below, we will implement an online version of the Perceptron algorithm, which is a simple yet effective linear classifier.

First, we define our Perceptron struct, which will hold the weights and learning rate:

struct Perceptron {
    weights: Vec<f64>,
    learning_rate: f64,
}

impl Perceptron {
    fn new(input_size: usize, learning_rate: f64) -> Self {
        Self {
            weights: vec![0.0; input_size + 1], // +1 for bias
            learning_rate,
        }
    }

    fn predict(&self, inputs: &[f64]) -> f64 {
        let mut sum = self.weights[0]; // bias term
        for (weight, &input) in self.weights.iter().skip(1).zip(inputs.iter()) {
            sum += weight * input;
        }
        if sum > 0.0 { 1.0 } else { 0.0 }
    }

    fn train(&mut self, inputs: &[f64], target: f64) {
        let prediction = self.predict(inputs);
        let error = target - prediction;

        self.weights[0] += self.learning_rate * error; // update bias
        for (i, &input) in inputs.iter().enumerate() {
            self.weights[i + 1] += self.learning_rate * error * input;
        }
    }
}

In this implementation, we define the Perceptron struct with a vector of weights, including a bias term. The predict method computes the dot product of the weights and inputs, outputting a binary prediction. The train method adjusts the weights based on the prediction error and the learning rate.

Now, let’s simulate an online learning scenario where we feed the Perceptron with streaming data. We will generate a simple dataset and continuously update the model:

fn main() {
    let mut perceptron = Perceptron::new(2, 0.1); // 2 input features

    // Simulated streaming dataset: (inputs, target)
    let dataset = vec![
        (vec![0.0, 0.0], 0.0),
        (vec![0.0, 1.0], 1.0),
        (vec![1.0, 0.0], 1.0),
        (vec![1.0, 1.0], 1.0),
    ];

    // Simulating streaming data
    for (inputs, target) in dataset.iter() {
        perceptron.train(inputs, *target);
        println!("Updated weights: {:?}", perceptron.weights);
    }

    // Testing the model
    let test_input = vec![1.0, 1.0];
    let prediction = perceptron.predict(&test_input);
    println!("Prediction for {:?}: {}", test_input, prediction);
}

In this example, we instantiate a Perceptron object and simulate a streaming dataset consisting of four input-target pairs. As each input is processed, the model updates its weights based on the prediction error. This allows the model to adapt continuously, reflecting the essence of online learning.

The practical implementation of online learning algorithms like the Perceptron in Rust showcases the robustness and efficiency of this programming language in handling large-scale machine learning tasks. By leveraging Rust's safety features and high performance, we can build scalable systems capable of processing and learning from data streams efficiently. As we delve deeper into the nuances of online learning, we can explore more sophisticated algorithms and strategies that enhance model adaptability, enabling us to tackle the complexities of non-stationary data effectively. This exploration will further strengthen our understanding of large-scale machine learning in Rust, paving the way for developing innovative solutions for real-world applications.

20.5. Large-Scale Model Deployment and Optimization link

Deploying large-scale machine learning models in production environments presents unique challenges and considerations that must be addressed to ensure efficiency, reliability, and performance. In this section, we will explore the fundamental ideas related to the deployment of these models, including aspects of latency, scalability, and fault tolerance. Furthermore, we will delve into conceptual ideas that highlight the challenges faced when deploying models at scale, as well as the importance of model optimization techniques such as quantization and pruning. Finally, we will provide practical examples of how to implement model deployment pipelines in Rust, leveraging tools like Docker and Kubernetes, while applying optimization techniques to enhance model performance.

Figure 4: Complexity of large-scale

When deploying large-scale machine learning models, latency becomes a critical factor. Low-latency responses are essential, especially for applications that require real-time predictions, such as autonomous vehicles or online recommendation systems. Scalability is another key consideration, as the system should be able to handle increasing loads seamlessly. This often requires distributed computing strategies, where the workload is shared across multiple machines or instances. Fault tolerance is equally important; systems must be designed to withstand failures and ensure continuous operation without significant downtime. Implementing redundancy, using load balancers, and employing graceful degradation strategies are some of the ways to achieve fault tolerance in large-scale deployments.

The deployment of models at scale introduces a range of challenges. One of the primary challenges is ensuring that the model performs consistently across different environments. Differences in hardware, software, and configurations can lead to discrepancies in model behavior. Furthermore, managing dependencies and versioning becomes complex in large-scale systems. Another challenge is the resource consumption of large models, which may require significant memory and processing power, making them impractical for deployment in certain contexts. Optimization techniques such as model quantization, which reduces the precision of the model parameters, and pruning, which eliminates unnecessary weights from the model, can help mitigate these issues. These techniques not only reduce the size of the model but also enhance inference speed, enabling faster predictions in production environments.

To maintain and monitor large-scale models, it is essential to have robust logging and monitoring mechanisms in place. This allows for real-time tracking of model performance, detection of anomalies, and identification of potential issues before they escalate. Tools such as Prometheus for monitoring and Grafana for visualization can be integrated into the deployment pipeline to provide valuable insights into the model's performance metrics. Additionally, implementing A/B testing can help evaluate new model versions against the current ones, allowing teams to make data-driven decisions when it comes to model updates and optimizations.

In a practical context, deploying machine learning models using Rust can be achieved by creating model deployment pipelines that integrate with containerization and orchestration tools. Docker can be used to create lightweight, portable containers that encapsulate the model and its dependencies. Below is a basic example of how to create a Dockerfile for a Rust application that serves a machine learning model:

# Use the official Rust image
FROM rust:latest

# Set the working directory
WORKDIR /usr/src/myapp

# Copy the source code
COPY . .

# Build the application
RUN cargo build --release

# Expose the port the app runs on
EXPOSE 8080

# Command to run the application
CMD ["./target/release/myapp"]

After building the Docker image, you can deploy it to a Kubernetes cluster. Kubernetes provides a robust platform for managing containerized applications, offering features like load balancing, scaling, and automatic failover. Below is an example of a Kubernetes deployment configuration for our Rust application:

apiVersion: apps/v1
kind: Deployment
metadata:
  name: rust-ml-model
spec:
  replicas: 3
  selector:
    matchLabels:
      app: rust-ml-model
  template:
    metadata:
      labels:
        app: rust-ml-model
    spec:
      containers:
      - name: rust-ml-model
        image: rust-ml-model:latest
        ports:
        - containerPort: 8080

In this configuration, we are creating a deployment with three replicas of our Rust machine learning application, ensuring that the application can handle incoming requests even if one or more instances fail. By utilizing Kubernetes, we can easily scale our application up or down based on load, and the orchestrator will manage the lifecycle of our containers.

In summary, deploying large-scale machine learning models in Rust involves a comprehensive understanding of various factors, including latency, scalability, and fault tolerance. The challenges of model deployment at scale can be addressed through optimization techniques such as quantization and pruning, alongside effective monitoring and maintenance strategies. By leveraging tools like Docker and Kubernetes, practitioners can implement robust deployment pipelines that ensure efficient and reliable model serving in production environments. The combination of Rust's performance characteristics and modern container orchestration technologies provides a solid foundation for building scalable machine learning applications.

20.6. Handling High-Dimensional Data link

In the realm of large-scale machine learning, one of the most intricate challenges that practitioners face is the handling of high-dimensional data. The term "high-dimensional data" refers to datasets where the number of features (or dimensions) significantly exceeds the number of observations. This situation can lead to what is known as the "curse of dimensionality," a phenomenon that complicates the modeling process and degrades the performance of machine learning algorithms. As the dimensionality of data increases, the volume of the space increases exponentially, making the available data sparse. This sparsity is problematic because most machine learning algorithms rely on the density of data to generalize effectively.

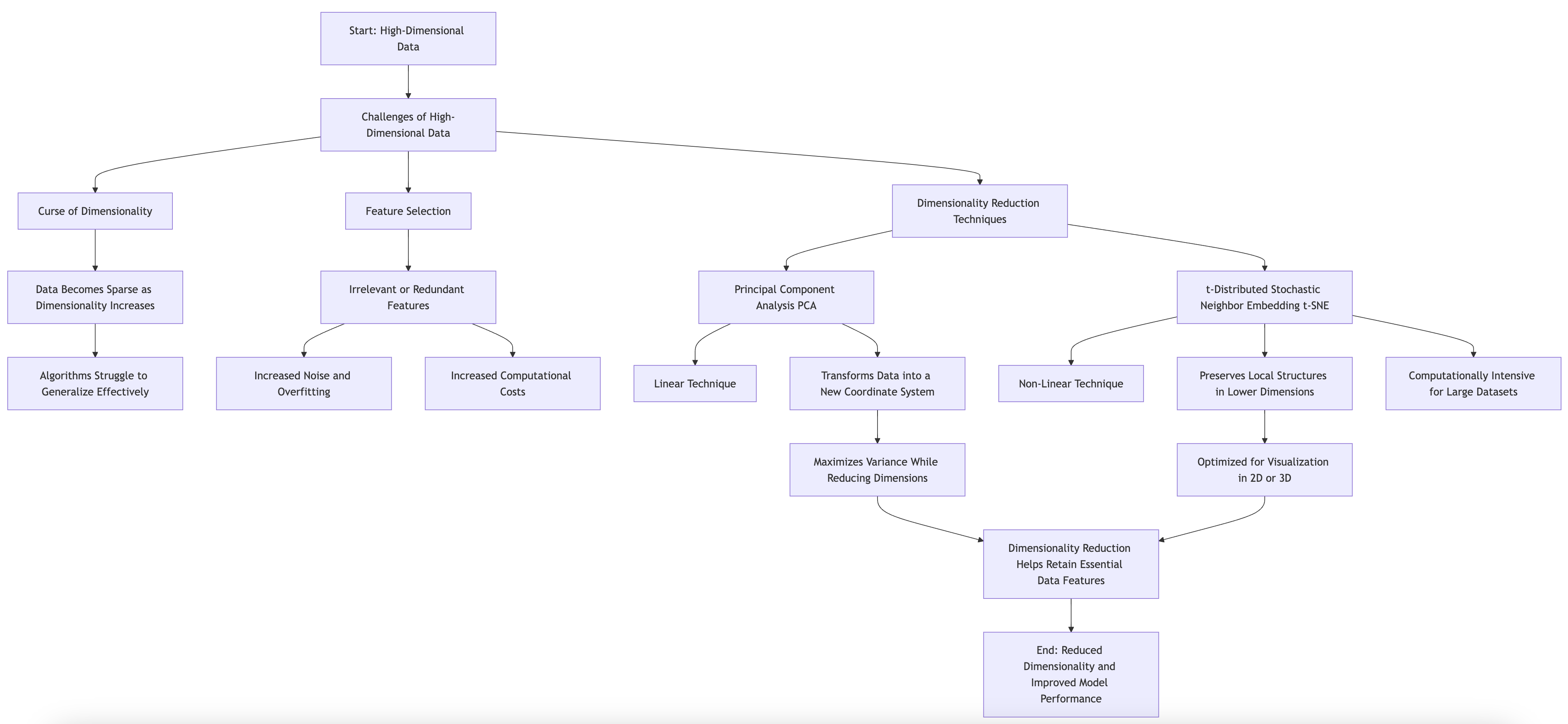
Figure 5: Handling high dimensionality data.

Another significant challenge posed by high-dimensional data is feature selection. Given an abundance of features, it becomes crucial to identify the most relevant ones that contribute meaningfully to the learning task. Irrelevant or redundant features can introduce noise, leading to overfitting, increased computational costs, and degraded model performance. Therefore, developing techniques that can effectively reduce dimensionality while retaining the essential characteristics of the data is vital.

Among the various techniques for dimensionality reduction, Principal Component Analysis (PCA) and t-Distributed Stochastic Neighbor Embedding (t-SNE) are two of the most frequently employed methods. PCA is a linear dimensionality reduction technique that transforms the data into a new coordinate system, where the greatest variance by any projection lies on the first coordinate (the principal component), the second greatest variance on the second coordinate, and so forth. This method is particularly useful when the goal is to maintain as much variance as possible while reducing the number of dimensions.

On the other hand, t-SNE is a non-linear technique specifically designed for visualizing high-dimensional data in lower dimensions (typically two or three). It works by converting the similarities between data points into joint probabilities and tries to minimize the divergence between the original and embedded distributions. While t-SNE excels in preserving local structures, it is computationally intensive, making it less suitable for very large datasets.

Implementing these dimensionality reduction techniques in Rust can provide significant advantages in terms of performance and safety due to Rust’s concurrency features and memory management capabilities. For instance, we can begin by implementing PCA in Rust. Below is a simplified version of how one might approach this task:

use nalgebra as na;
use na::{DMatrix, DVector};

fn pca(data: &DMatrix<f64>, num_components: usize) -> DMatrix<f64> {
    // Step 1: Center the data
    let mean = data.column_mean();
    let centered_data = data - DMatrix::from_diagonal(&mean);

    // Step 2: Compute the covariance matrix
    let covariance_matrix = &centered_data.transpose() * &centered_data / (data.nrows() as f64 - 1.0);

    // Step 3: Eigen decomposition
    let eig = na::linalg::SymmetricEigen::new(covariance_matrix);
    let eigenvalues = eig.eigenvalues;
    let eigenvectors = eig.eigenvectors;

    // Step 4: Sort eigenvalues and eigenvectors
    let mut indices: Vec<_> = (0..eigenvalues.len()).collect();
    indices.sort_by(|&i, &j| eigenvalues[j].partial_cmp(&eigenvalues[i]).unwrap());

    // Step 5: Select the top k eigenvectors
    let top_eigenvectors = eigenvectors.select_columns(&indices[..num_components]);

    // Step 6: Project the data onto the new subspace
    let reduced_data = centered_data * top_eigenvectors;
    reduced_data
}

In this code snippet, we first center the data by subtracting the mean, compute the covariance matrix, and then perform eigen decomposition. Eigenvalues and eigenvectors are sorted, and the top num_components are selected to form a new subspace onto which we project our data. This implementation leverages the nalgebra crate, which is essential for efficient matrix operations in Rust.

On the other hand, if we want to apply t-SNE for visualizing high-dimensional datasets, the implementation can be quite complex due to the algorithm's nature. However, we can leverage existing libraries like ndarray and ndarray-rand to help with the mathematical operations involved. The following pseudocode provides a high-level overview of how one might structure a t-SNE implementation:

fn tsne(data: &DMatrix<f64>, perplexity: f64, num_dimensions: usize) -> DMatrix<f64> {
    // Step 1: Compute pairwise affinities in the original space
    let affinities = compute_affinities(data, perplexity);
    
    // Step 2: Randomly initialize points in the lower-dimensional space
    let mut low_dim_data = random_initialization(data.nrows(), num_dimensions);

    // Step 3: Optimize the positions in the low-dimensional space
    for _ in 0..num_iterations {
        // Compute low-dimensional affinities
        let low_dim_affinities = compute_low_dim_affinities(&low_dim_data);
        
        // Compute the gradient
        let gradient = compute_gradient(&affinities, &low_dim_affinities, &low_dim_data);
        
        // Update the positions
        low_dim_data -= learning_rate * gradient;
    }

    low_dim_data
}

In this high-level pseudocode, we compute pairwise affinities in the original high-dimensional space based on the perplexity parameter, which controls the balance between local and global aspects of the dataset. We would then randomly initialize the points in a lower-dimensional space, iteratively optimize their positions by minimizing the divergence between high-dimensional and low-dimensional affinities, which is done through gradient descent.

Evaluating the impact of dimensionality reduction techniques on model performance is crucial. One can assess performance using metrics such as accuracy, F1 score, or area under the ROC curve (AUC) after training models on both the original and reduced datasets. It is essential to balance computational efficiency with model accuracy, especially in large-scale applications where both speed and performance are paramount. Reducing dimensionality can lead to faster training times and less memory consumption, but it may also lead to the loss of important information if not handled judiciously.

In conclusion, handling high-dimensional data in large-scale machine learning requires a nuanced understanding of the underlying challenges, such as the curse of dimensionality and feature selection. By employing techniques like PCA and t-SNE and implementing them in Rust, we can effectively reduce dimensionality while maintaining model performance and addressing the trade-offs inherent in these processes. The ability to manage high-dimensional data adeptly can lead to more robust models that are both efficient and accurate, ultimately enhancing the capabilities of machine learning applications.

20.7. Scalability in Distributed Machine Learning Systems link

In the realm of machine learning, scalability stands as one of the most critical challenges, particularly when transitioning from single-node systems to distributed environments. As datasets grow in size and complexity, the need for efficient distributed machine learning systems becomes paramount. This section delves deep into the fundamental challenges, the conceptual architectures employed in distributed machine learning, and practical implementations in Rust, catering to large-scale datasets while ensuring performance and fault tolerance.

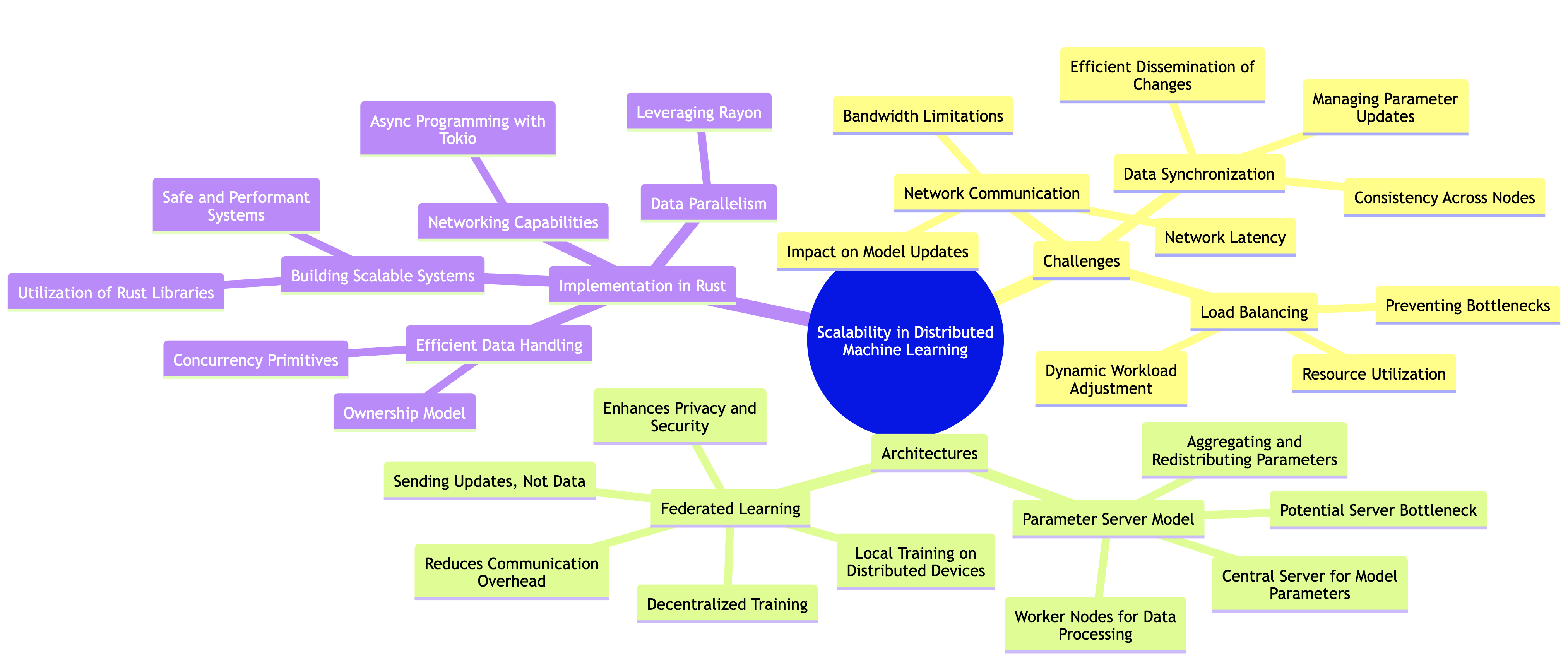
Figure 6: Complexity map of scalability in distributed ML systems.

The fundamental challenges of scalability in distributed machine learning systems primarily revolve around network communication, data synchronization, and load balancing. As data is distributed across multiple nodes, the efficiency of communication between these nodes can significantly impact the overall performance of the system. Network latency and bandwidth limitations often hinder the speed at which models can be updated and refined. Additionally, data synchronization becomes critical; as different nodes process data concurrently, ensuring that all nodes have a consistent view of the model parameters is essential for the integrity of the learning process. This requires robust mechanisms to manage updates and disseminate changes across the distributed network effectively.

Load balancing is another key aspect of scalability that cannot be overlooked. In a distributed setting, it is vital to ensure that no single node becomes a bottleneck due to an uneven distribution of workload. This imbalance can lead to underutilization of resources and prolonged training times. Implementing strategies that dynamically adjust the workload based on current node performance and data distribution is crucial for maintaining efficiency in large-scale machine learning tasks.

Conceptually, distributed machine learning is often structured around specific architectures designed to tackle these challenges. One prevalent architecture is the parameter server model. In this design, a central server maintains the model parameters, while worker nodes are responsible for processing data and computing gradients. The workers communicate their updates to the parameter server, which aggregates these changes and redistributes the updated parameters back to the workers. This architecture simplifies the synchronization of model parameters but can introduce its own latency issues due to the central server becoming a potential bottleneck.

Federated learning is another innovative approach that promotes scalability by decentralizing the training process. Instead of centralizing data and model parameters, federated learning allows models to be trained locally on distributed devices, such as mobile phones or edge devices. The devices compute updates based on their local data and send only the updates back to a central server, which aggregates these updates to improve the global model. This not only reduces the amount of data that needs to be communicated but also enhances privacy and security by keeping sensitive data on the local devices.

Implementing distributed machine learning in Rust requires a combination of efficient data handling, networking capabilities, and robust concurrency management. Rust's ownership model and concurrency primitives provide an excellent foundation for building scalable systems. By leveraging libraries such as tokio for asynchronous programming and rayon for data parallelism, we can create a distributed machine learning system that effectively utilizes resources while maintaining safety and performance.

To illustrate a practical implementation, let’s consider a simplified scenario where we want to train a linear regression model using a distributed approach. We will divide our dataset across multiple nodes and implement a basic parameter server architecture. Below is a simple example of how this could be structured in Rust.

use std::sync::{Arc, Mutex};
use tokio::{io::AsyncReadExt, net::TcpListener};
// use tokio::prelude::*;
use std::collections::HashMap;

#[derive(Clone)]
struct ParameterServer {
    parameters: Arc<Mutex<HashMap<String, f64>>>,
}

impl ParameterServer {
    fn new() -> Self {
        ParameterServer {
            parameters: Arc::new(Mutex::new(HashMap::new())),
        }
    }

    fn update_parameters(&self, updates: HashMap<String, f64>) {
        let mut params = self.parameters.lock().unwrap();
        for (key, value) in updates {
            *params.entry(key).or_insert(0.0) += value;
        }
    }

    fn get_parameters(&self) -> HashMap<String, f64> {
        self.parameters.lock().unwrap().clone()
    }
}

#[tokio::main]
async fn main() {
    let server = ParameterServer::new();

    let listener = TcpListener::bind("127.0.0.1:8080").await.unwrap();
    println!("Parameter server running on 127.0.0.1:8080");

    loop {
        let (mut socket, _) = listener.accept().await.unwrap();
        let server_clone = server.clone();
        
        tokio::spawn(async move {
            let mut buf = Vec::new();
            socket.read_to_end(&mut buf).await.unwrap();
            let updates: HashMap<String, f64> = bincode::deserialize(&buf).unwrap();
            server_clone.update_parameters(updates);
        });
    }
}

In this example, we define a ParameterServer struct that manages model parameters using a shared HashMap. We create an asynchronous TCP server that listens for incoming connections, simulating the workers sending their updates to the server. Upon receiving updates, the server aggregates them into its parameter store.

In addition to this basic setup, evaluating the system’s scalability involves testing with larger datasets and measuring performance metrics such as training time, the efficiency of parameter updates, and the system's ability to handle node failures. By introducing fault tolerance mechanisms, such as checkpointing the model parameters and implementing retry logic for failed updates, we can further enhance the robustness of our distributed machine learning system.

In conclusion, scalability in distributed machine learning systems is a multifaceted problem that encompasses network communication, data synchronization, and load balancing. By understanding the conceptual frameworks like parameter servers and federated learning, and implementing them using Rust's capabilities, we can build efficient and robust systems capable of handling large-scale machine learning tasks effectively. As we continue to explore distributed machine learning, the strategies and implementations discussed will serve as a foundation for building more complex and scalable solutions.

20.8. Conclusion link

Chapter 20 equips you with the knowledge and tools necessary to tackle the challenges of Large-Scale Machine Learning. By mastering these techniques in Rust, you will be able to build, deploy, and optimize models that can handle massive datasets efficiently, ensuring that your machine learning applications are scalable, robust, and ready for real-world deployment.

20.8.1. Further Learning with GenAI link

By exploring these prompts, you will deepen your knowledge of the theoretical foundations, practical applications, and advanced techniques in large-scale learning, equipping you to build and optimize robust machine learning models that can handle massive datasets.

• Explain the challenges of scaling machine learning models to large datasets. How do computational complexity, memory constraints, and data distribution affect model performance, and what strategies can be used to address these issues? Implement a basic large-scale machine learning task in Rust.

• Discuss the concept of data parallelism in large-scale machine learning. How does data partitioning and parallel processing help in scaling machine learning algorithms, and what are the trade-offs involved? Implement data parallelism in Rust using libraries like Rayon.

• Analyze the role of Stochastic Gradient Descent (SGD) in large-scale learning. How does SGD improve the efficiency of gradient descent on large datasets, and what are the advantages and challenges of using SGD and its variants? Implement SGD in Rust and apply it to a large-scale dataset.

• Explore the benefits of online learning and incremental algorithms for large-scale machine learning. How do these algorithms handle streaming data and continuously update models, and what challenges arise in non-stationary environments? Implement an online learning algorithm in Rust and apply it to a streaming dataset.

• Discuss the challenges of deploying large-scale machine learning models in production environments. How do latency, scalability, and fault tolerance impact model deployment, and what strategies can be used to optimize model performance in production? Implement a model deployment pipeline in Rust.

• Analyze the impact of high-dimensional data on large-scale machine learning. How does the curse of dimensionality affect model performance, and what techniques can be used for dimensionality reduction in large-scale settings? Implement dimensionality reduction techniques in Rust for a high-dimensional dataset.

• Explore the architecture of distributed machine learning systems. How do distributed frameworks like parameter servers and federated learning handle the challenges of scalability, data synchronization, and load balancing in large-scale machine learning? Implement a distributed machine learning system in Rust.

• Discuss the trade-offs between synchronous and asynchronous parallelism in distributed machine learning. How do these approaches differ in terms of communication overhead, convergence speed, and fault tolerance? Implement both synchronous and asynchronous parallelism in Rust and compare their performance.

• Analyze the role of model optimization techniques like quantization and pruning in large-scale machine learning. How do these techniques reduce model size and improve inference speed, and what are the trade-offs in terms of accuracy? Implement model optimization techniques in Rust.

• Explore the concept of federated learning for large-scale machine learning. How does federated learning enable decentralized model training across multiple devices or nodes, and what are the challenges of ensuring data privacy and model consistency? Implement federated learning in Rust and apply it to a distributed dataset.

• Discuss the importance of load balancing in distributed machine learning systems. How does load balancing ensure efficient utilization of computational resources, and what strategies can be used to distribute the workload evenly across nodes? Implement load balancing in Rust for a distributed machine learning task.

• Analyze the impact of communication overhead in distributed machine learning. How does network communication affect the performance of distributed models, and what techniques can be used to minimize communication latency and bandwidth usage? Implement communication optimization techniques in Rust.

• Explore the use of scalable algorithms in large-scale machine learning. How do algorithms like scalable k-means or scalable deep learning models handle massive datasets, and what are the challenges of ensuring convergence and stability? Implement a scalable machine learning algorithm in Rust.

• Discuss the challenges of fault tolerance in large-scale machine learning systems. How does fault tolerance impact the reliability and robustness of distributed models, and what strategies can be used to recover from failures in a distributed environment? Implement fault tolerance mechanisms in Rust for a large-scale machine learning system.

• Analyze the role of memory management in large-scale machine learning. How do memory constraints affect the performance and scalability of models, and what techniques can be used to manage memory efficiently in Rust? Implement memory management techniques in Rust for a large-scale dataset.

• Explore the concept of model parallelism in large-scale machine learning. How does model parallelism differ from data parallelism, and what are the advantages and challenges of partitioning a model across multiple nodes? Implement model parallelism in Rust and compare it with data parallelism.

• Discuss the challenges of integrating large-scale machine learning models with real-time systems. How do real-time constraints affect model deployment and performance, and what strategies can be used to ensure timely and accurate predictions? Implement a real-time machine learning system in Rust.

• Analyze the impact of hardware acceleration on large-scale machine learning. How do GPUs, TPUs, and other accelerators improve the efficiency of large-scale models, and what are the challenges of leveraging these resources in Rust? Implement hardware acceleration techniques in Rust for a large-scale machine learning task.

• Explore the future directions of research in large-scale machine learning. What are the emerging trends and challenges in this field, and how can advances in distributed computing, optimization algorithms, and hardware technologies contribute to the development of more scalable and efficient machine learning models? Implement a cutting-edge large-scale machine learning technique in Rust.

Each prompt encourages you to think critically about the scalability challenges in machine learning and to apply your knowledge to create efficient and scalable solutions.

20.8.2. Hands On Practices link

These exercises are designed to be challenging and in-depth, requiring you to apply both theoretical knowledge and practical skills in Rust.